2021年北京通州区首都师范大学附属中学八年级上期末数学试卷

这是一份2021年北京通州区首都师范大学附属中学八年级上期末数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共8小题；共40分）
1. 下列式子为最简二次根式的是
A. 13B. 30C. 0.3D. 20

2. 81 的算术平方根是
A. 3B. −3C. ±3D. 6

3. 下列图形中对称轴的条数最少的是
A. 正五边形B. 等边三角形
C. 正方形D. 长宽不等的长方形

4. 已知分式 x−1x+2x2−1 的值为 0，那么 x 的值是
A. −1B. −2C. 1D. 1 或 −2

5. 据中新社 2017 年 10 月 8 日报道，2017 年我国粮食总产量达到 736000000 吨，将 736000000 用科学记数法表示为
A. 736×106B. 73.6×107C. 7.36×108D. 0.736×109

6. 如图，在 △ABC 中，AB=AC，AB 的垂直平分线交 AB 于点 E，交 BC 于点 F，连接 AF，若 ∠FAC=215∠B，则 ∠FAB 的度数为
A. 25∘B. 30∘C. 35∘D. 50∘

7. 如图，在等边三角形 ABC 中，D 是 AC 边上的中点，延长 BC 到点 E，使 CE=CD，则 ∠E 的度数为
A. 15∘B. 20∘C. 30∘D. 40∘

8. 下列随机事件：①在一副扑克牌中，抽一张是红桃；②抛掷一枚质地均匀的骰子，朝上一面的点数是偶数；③抛一枚质地均匀的硬币，正面朝上；④不透明的袋子中有除颜色外完全相同的红球和白球各 2 个，摸出一个是白球，其中，概率为 12 的是
A. ①③B. ①②③C. ②③④D. ①②③④

二、填空题（共8小题；共40分）
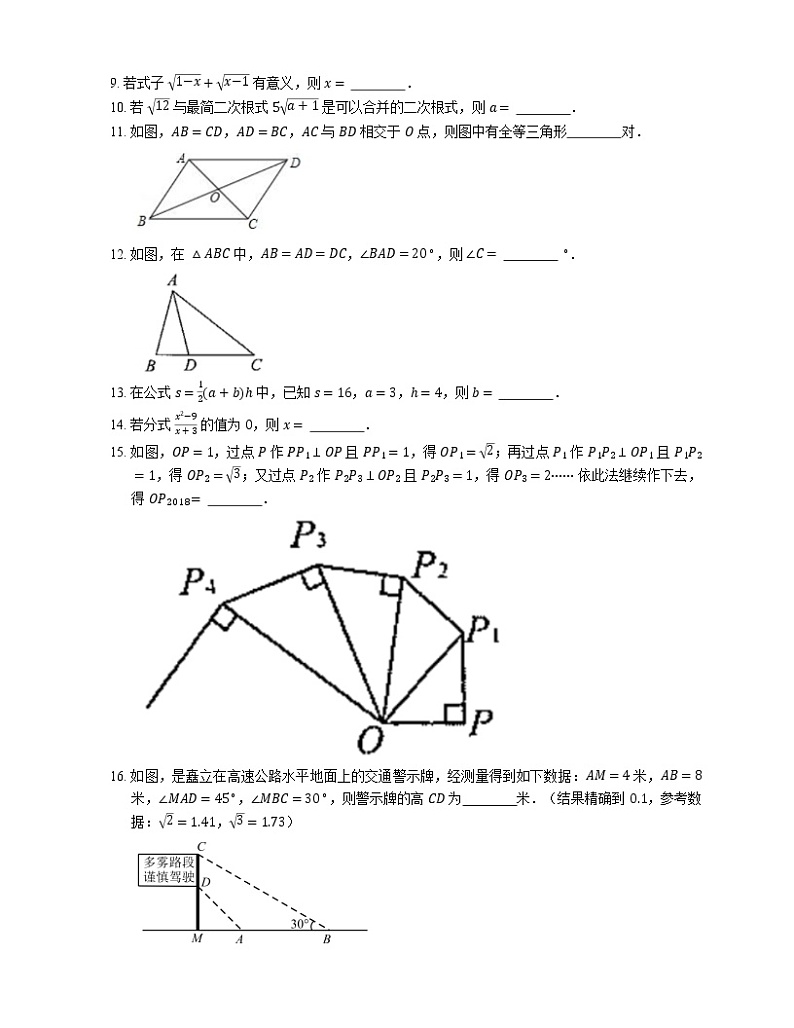
9. 若式子 1−x+x−1 有意义，则 x= ．

10. 若 12 与最简二次根式 5a+1 是可以合并的二次根式，则 a= ．

11. 如图，AB=CD，AD=BC，AC 与 BD 相交于 O 点，则图中有全等三角形 对．

12. 如图，在 △ABC 中，AB=AD=DC，∠BAD=20∘，则 ∠C= ∘．

13. 在公式 s=12a+bh 中，已知 s=16，a=3，h=4，则 b= ．

14. 若分式 x2−9x+3 的值为 0，则 x= ．

15. 如图，OP=1，过点 P 作 PP1⊥OP 且 PP1=1，得 OP1=2；再过点 P1 作 P1P2⊥OP1 且 P1P2=1，得 OP2=3；又过点 P2 作 P2P3⊥OP2 且 P2P3=1，得 OP3=2⋯⋯ 依此法继续作下去，得 OP2018= ．

16. 如图，是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM=4 米，AB=8 米，∠MAD=45∘，∠MBC=30∘，则警示牌的高 CD 为 米．（结果精确到 0.1，参考数据：2=1.41，3=1.73）

三、解答题（共12小题；共156分）
17. 计算：12−3−412+48−24÷6．

18. 计算：m+2nm−2n−m+3n2．

19. 化简：4xx2−4−2x−2−1．
圆圆的解答如下：4xx2−4−2x−2−1=4x−2x+2−x2−4=−x2+2x
圆圆的解答正确吗?如果不正确，写出正确的答案．

20. 如图，∠B=∠E，BF=EC，AC∥DF．求证：△ABC≌△DEF．

21. 如图，在 △ABC 和 △ADE 中，AB=AD，AC=AE，∠1=∠2．
（1）求证：△ABC≌△ADE．
（2）找出图中与 ∠1，∠2 相等的角（直接写出结论，不需证明）．

22. 八年级学生到距离学校 15 千米的农科所参观，一部分学生骑自行车先走，走了 40 分钟后，其余同学乘汽车出发，结果两者同时到达．若汽车的速度是骑自行车同学速度的 3 倍，求骑自行车同学的速度?

23. 21−x2=11+x．

24. 先化简：x−1x−2−x+2x÷4−xx2−4x+4，然后选择一个合适的 x 值代入求值．

25. （1）化简 x−1x÷(x−1x) ．
（2）解方程：2x2x−1+51−2x=3．

26. 如图，AB=AE，AB∥DE，∠DAB=70∘，∠E=40∘．
（1）求 ∠DAE 的度数；
（2）若 ∠B=30∘，求证：AD=BC．

27. 请回答下列问题．
（1）如图①，点 A，E，F，C 在同一条直线上，AE=CF，过点 E，F 分别作 DE⊥AC，BF⊥AC，且 AB=CD，连接 BD，交 AC 于点 G，求证：EG=FG．
（2）若将 △DEC 沿 AC 方向移动至图② 时，其余条件不变，则 EG=FG 是否仍然成立?请说明理由．

28. 复习“平行线”内容时，老师布置了一道思考题：如图所示在 △ABC 中，点 D，E，F 分别是 AB，AC，BC 上的点，且 DE⊥AB，EF⊥DE，点 P 是 FC 上一点，直线 DP 交直线 EF 于点 G，试探究 ∠BDP 与 ∠EGP 之间的数量关系．
（1）请你完成这道思考题．
（2）若将题中的条件“DE⊥AB，EF⊥DE，点 P 是 FC 上一点”改为“∠AED=∠C，∠B=∠DEF，点 P 是 BC 上一点（点 P 不与点 F 重合）”，其他条件均不变，则（1）中的结论是否仍然成立?请在备用图上画出图形，作出判断并说明理由．
答案
第一部分
1. B【解析】A、 13=33，不是最简二次根式，故本选项不符合题意；
B、 30 是最简二次根式，故本选项不符合题意；
C、 0.3=3010，不是最简二次根式，故本选项不符合题意；
D、 20=25，不是最简二次根式，故本选项不符合题意．
2. A【解析】∵81=9，
∴81 的算术平方根是 9=3．
3. D
4. B
5. C
6. A【解析】因为 AB=AC，
所以 ∠B=∠C，
因为 EF 垂直平分 AB，
所以 BF=AF，
所以 ∠BAF=∠B=∠C，
因为 ∠FAC=215∠B，
所以 215∠B+3∠B=180∘，
所以 ∠B=25∘，
所以 ∠FAB 的度数为 25∘，
故选：A．
7. C
8. C【解析】①在一副扑克牌中，抽一张是红桃的概率是 1354；②抛掷一枚质地均匀的骰子，朝上一面的点数是偶数的概率是 12；③抛一枚质地均匀的硬币，正面朝上的概率是 12；④不透明的袋子中有除颜色外完全相同的红球和白球各 2 个，摸出一个是白球的概率是 24=12，所以符合题意的为②③④．
第二部分
9. 1
10. 2
【解析】∵12=23，12 与最简二次根式 5a+1 可以合并，
∴a+1=3，
∴a=2．
11. 4
【解析】∵ AB=CD，AD=BC，
又 BD=DB，
∴ △ABD≌△CDB，
进而可得 △ADC≌△ABC，△AOD≌△BOC，△ABO≌△CDO，共 4 对．故答案为 4．
12. 40
13. 5
14. 3
15. 2019
16. 2.9
【解析】由题意可得：
∵AM=4 米，∠MAD=45∘，
∴DM=4 m，
∵AM=4 米，AB=8 米，
∴MB=12 米，
∵∠MBC=30∘，
∴BC=2MC，
∴MC2+MB2=2MC2，
MC2+122=2MC2，
∴MC=43，
则 DC=43−4≈2.9（米）．
第三部分
17. 原式=2+3−22+48÷6−24÷6=2+3−22+22−2=3.
18. 原式=m2−4n2−m2+6mn+9n2=m2−4n2−m2−6mn−9n2=−13n2−6mn.
19. 圆圆的解答错误，正确解法：
4xx2−4−2x−2−1=4xx−2x+2−2x+2x−2x+2−x−2x+2x−2x+2=4x−2x−4−x2+4x−2x+2=2x−x2x−2x+2=−xx+2.
20. ∵AC∥DF，
∴∠ACB=∠DFE，
∵BF=CE，
∴BC=EF，
在 △ABC 和 △DEF 中，∠B=∠E,BC=EF,∠ACB=∠DFE,
∴△ABC≌△DEFASA．
21. （1） ∵∠1=∠2，
∴∠1+∠DAC=∠2+∠DAC，即 ∠BAC=∠DAE，
在 △ABC 和 △ADE 中，
AB=AD,∠BAC=∠DAE,AC=AE,
∴△ABC≌△ADESAS．
（2） ∠NFC，∠MFD．
【解析】∵△ABC≌△ADE，
∴∠B=∠D，
∵∠AMB=∠DMF，
∴∠1=∠MFD，
∵∠MFD=∠NFC，
∴∠1=∠NFC，
∴ 与 ∠1，∠2 相等的角有 ∠NFC，∠MFD．
22. 设骑自行车的速度是 x 千米/小时，
15x=153x+4060.
解得，
x=15.
经检验 x=15 是方程的解，且符合实际意义．
答：骑自行车的同学的速度是 15 千米/小时．
23. 无解
24. 原式=xx−1xx+2−x−2x+2xx−2⋅x−224−x=4−xxx−2⋅x−224−x=x−2x,
把 x=1 代入得 原式=1−21=−1．
25. （1） 原式
=x−1x÷x2−1x=1x+1
（2） 解：去分母得 2x−5=3(2x−1) ，
即 2x−5=6x−3，
∴4x=−2 ，
x=−12 ，
当 x=−12 时， 2x−1≠0
所以x=−12 是原方程的解．
26. （1） 因为 AB∥DE，∠E=40∘，
所以 ∠EAB=40∘．
因为 ∠DAB=70∘，
所以 ∠DAE=30∘．
（2） 在 △ADE 与 △BCA 中，
∠DEA=∠BAC,AB=AE,∠DAE=∠B,
所以 △ADE≌△BCAASA，
所以 AD=BC．
27. （1） ∵DE⊥AC，BF⊥AC，
∴∠DEF=∠BFE=90∘．
∵AE=CF，
∴AE+EF=CF+EF，即 AF=CE．
在 Rt△ABF 和 Rt△CDE 中，AB=CD,AF=CE,
∴Rt△ABF≌Rt△CDE（HL）．
∴BF=DE．
在 △DEG 和 △BFG 中，∠DEG=∠BFG,∠DGE=∠BGF,DE=BF,
∴△DEG≌△BFGAAS．
∴EG=FG．
（2） EG=FG 依然成立．
理由：∵DE⊥AC，BF⊥AC，
∴∠BFA=∠DEC=90∘，
∵AE=CF，
∴AE−EF=CF−EF，即 AF=CE．
在 Rt△ABF 和 Rt△CDE 中，AB=CD,AF=CE,
∴Rt△ABF≌Rt△CDE（HL）．
∴BF=DE．
在 △DEG 和 △BFG 中，∠DEG=∠BFG,∠DGE=∠BGF,DE=BF,
∴△DEG≌△BFGAAS．
∴EG=FG．
28. （1） ∠BDP+∠EGP=180∘．理由如下：
因为 DE⊥AB，EF⊥DE，
所以 AB∥EF，
所以 ∠BDP+∠DGF=180∘，
又因为 ∠DGF=∠EGP，
所以 ∠BDP+∠EGP=180∘．
（2） 当点 P 在线段 BF 上时，∠BDP=∠EGP：当点 P 在线段 CF 上时，∠BDP+∠EGP=180∘．理由如下：
因为 ∠AED=∠C，
所以 DE∥BC，
所以 ∠ADE=∠B．
又因为 ∠B=∠DEF，
所以 ∠ADE=∠DEF，
所以 AB∥EF．
如图 1 所示，
因为 AB∥EF，
所以 ∠BDP=∠EGP．
如图 2所示，
因为 AB∥EF，
所以 ∠BDP+∠DGF=180∘，
又因为 ∠DGF=∠EGP，
所以 ∠BDP+∠EGP=180∘．