

第6章 第1节 数列的概念与简单表示法教案
展开一、教材概念·结论·性质重现
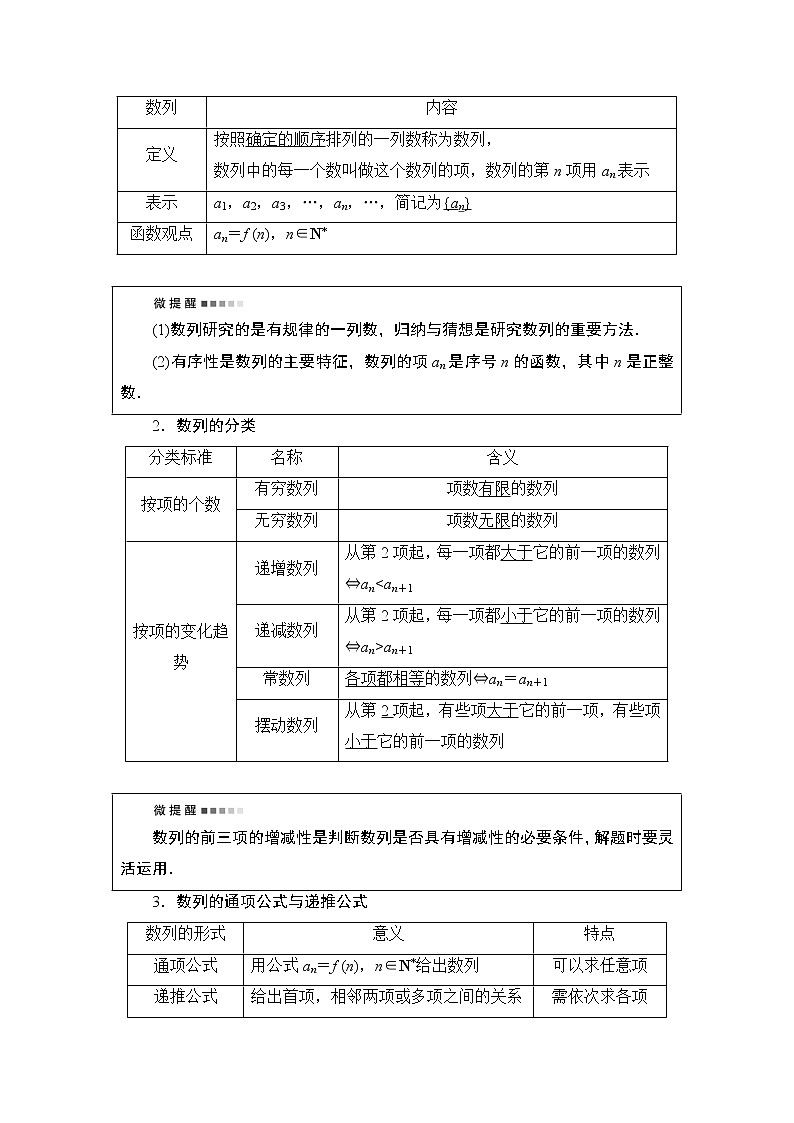
1.数列的概念与表示
(1)数列研究的是有规律的一列数,归纳与猜想是研究数列的重要方法.
(2)有序性是数列的主要特征,数列的项an是序号n的函数,其中n是正整数.
2.数列的分类
数列的前三项的增减性是判断数列是否具有增减性的必要条件,解题时要灵活运用.
3.数列的通项公式与递推公式
由数列的递推公式求数列的通项公式是高频考点.
4.数列的前n项和
(1)表示:在数列{an}中,Sn=a1+a2+…+an叫做数列的前n项和.
(2)an与Sn的关系:若数列{an}的前n项和为Sn,则an=eq \b\lc\{\rc\ (\a\vs4\al\c1(S1,n=1,,Sn-Sn-1,n≥2.))
(1)求数列的前n项和,从首项起,以后各项依次相加,其中项数是易错点.
(2)由Sn求an的三个步骤:①求a1=S1;②当n≥2时,求an=Sn-Sn-1;③验证首项.
二、基本技能·思想·活动体验
1.判断下列说法的正误,对的打“√”,错的打“×”.
(1)数列1,2,3与3,2,1是同一个数列.(×)
(2)在数列{an}中,对于任意正整数m,n,am+n=amn+1,若a1=1,则a2=2.(√)
(3)根据数列的前几项归纳出数列的通项公式可能不止一个.(√)
(4)任何一个数列不是递增数列,就是递减数列.(×)
(5)如果数列{an}的前n项和为Sn,则对∀n∈N*,都有an=Sn-Sn-1.(×)
2.设数列{an}的前n项和Sn=n2,则a8的值为( )
A.15 B.16 C.49 D.64
A 解析:因为Sn=n2,所以a1=S1=1.
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.
当n=1时符合上式,
所以an=2n-1,所以a8=2×8-1=15.
3.(多选题)已知数列的通项公式为an=n2-10n+16,则下列说法正确的是( )
A.数列{an}是递增数列
B.数列{an}是递减数列
C.数列{an}中的最小项是第5项
D.数列{an}前5项递减,以后各项递增
CD 解析:由于通项公式an=n2-10n+16=(n-5)2-9,所以数列{an}中的最小项是第5项,数列{an}的前5项递减,以后各项递增.
4.在数列1,1,2,3,5,8,13,21,x,55,…中,x=________.
34 解析:通过观察数列各项的规律,发现从第三项起,每项都等于它前两项之和,因此x=13+21=34.
5.已知an=n2+λn,且对于任意的n∈N*,数列{an}是递增数列,则实数λ的取值范围是________.
(-3,+∞) 解析:因为{an}是递增数列,所以对任意的n∈N*,都有an+1>an,即(n+1)2+λ(n+1)>n2+λn,
整理得2n+1+λ>0,即λ>-(2n+1).(*)
因为n≥1,所以-(2n+1)≤-3,要使不等式(*)恒成立,只需λ>-3.
考点1 由数列的前几项求数列的通项——基础性
1.(2020·乌鲁木齐米东区期中)数列-1,3,-6,10,…的一个通项公式是( )
A.an=(-1)nn2-(n-1)
B.an=(-1)n+1(n2-1)
C.an=(-1) n eq \f(nn+1,2)
D.an=(-1)n-1 eq \f(nn-1,2)
C 解析:设此数列为an,可得每一项的符号为(-1)n,且|an|=eq \f(nn+1,2),所以an=(-1)n eq \f(nn+1,2).
2.已知数列eq \r(5),eq \r(11),eq \r(17),eq \r(23),eq \r(29),…,则5eq \r(5)是它的( )
A.第19项B.第20项
C.第21项D.第22项
C 解析:数列eq \r(5),eq \r(11),eq \r(17),eq \r(23),eq \r(29),…中的各项可变形为eq \r(5),eq \r(5+6),eq \r(5+2×6),eq \r(5+3×6),eq \r(5+4×6),…,所以通项公式为an=eq \r(5+6n-1)=eq \r(6n-1),令eq \r(6n-1)=5eq \r(5),得n=21.
3.数列{an}的前4项是eq \f(3,2),1,eq \f(7,10),eq \f(9,17),则这个数列的一个通项公式是an=________.
eq \f(2n+1,n2+1) 解析:数列{an}的前4项可变形为eq \f(2×1+1,12+1),eq \f(2×2+1,22+1),eq \f(2×3+1,32+1),eq \f(2×4+1,42+1),故它的一个通项公式an=eq \f(2n+1,n2+1).
4.一个数列{an}的前4项是0.8,0.88,0.888,0.888 8,则这个数列的一个通项公式是an=________.
eq \f(8,9)eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,10n))) 解析:数列变为eq \f(8,9)eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,10))),eq \f(8,9)eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,102))),eq \f(8,9)eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,103))),…,故它的一个通项公式an=eq \f(8,9)eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,10n))).
由数列的前几项求数列的通项的策略
根据所给数列的前几项求其通项时,需仔细观察、对比、分析,从整体到局部多角度归纳、联想.抓住以下几个方面的特征:
(1)分式中分子、分母的各自特征;
(2)相邻项的联系特征;
(3)拆项后的各部分特征;
(4)符号特征.
考点2 由Sn与an的关系求通项——应用性
(1)已知数列{an}的前n项和Sn=2n2-3n,则an=________.
4n-5 解析:a1=S1=2-3=-1,
当n≥2时,an=Sn-Sn-1=(2n2-3n)-[2(n-1)2-3(n-1)]=4n-5,
由于a1也适合此等式,所以an=4n-5.
(2)(2019·上海卷)已知数列{an}前n项和为Sn,且满足Sn+an=2,则S5=________.
eq \f(31,16) 解析:当n=1时,S1+a1=2,所以a1=1.
当n≥2时,由Sn+an=2得Sn-1+an-1=2,
两式相减得an=eq \f(1,2)an-1(n≥2),
所以{an}是以1为首项,eq \f(1,2)为公比的等比数列,
所以Sn=eq \f(1×\b\lc\[\rc\](\a\vs4\al\c1(1-\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up8(n))),1-\f(1,2)),
所以S5=eq \f(1×\b\lc\[\rc\](\a\vs4\al\c1(1-\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up8(5))),1-\f(1,2))=eq \f(31,16).
1.本例(1)条件变为“Sn=3n+1”,求数列{an}的通项公式.
解:当n=1时,a1=S1=3+1=4;
当n≥2时,an=Sn-Sn-1=(3n+1)-(3n-1+1)=2×3n-1.
当n=1时,2×31-1=2≠a1,
所以an=eq \b\lc\{\rc\ (\a\vs4\al\c1(4,n=1,,2×3n-1,n≥2.))
2.本例(2)条件变为“Sn=2an+1”,求S6.
解:因为Sn=2an+1,当n≥2时,Sn-1=2an-1+1,
所以an=Sn-Sn-1=2an-2an-1(n≥2),
即an=2an-1(n≥2).
当n=1时,a1=S1=2a1+1,得a1=-1.
所以数列{an}是首项a1=-1,公比q=2的等比数列,
所以Sn=eq \f(a11-qn,1-q)=eq \f(-1×1-2n,1-2)=1-2n,
所以S6=1-26=-63.
已知Sn求an的步骤
(1)先利用a1=S1求出a1;
(2)用n-1替换Sn中的n得到一个新的关系,利用an=Sn-Sn-1(n≥2)便可求出当n≥2时an的表达式;
(3)注意检验n=1时的表达式是否可以与n≥2的表达式合并.
已知数列{an},a1+3a2+32a3+…+3n-1an=eq \f(n,3),求数列{an}的通项公式.
解:因为a1+3a2+32a3+…+3n-1an=eq \f(n,3),①
则当n≥2时,
a1+3a2+32a3+…+3n-2an-1=eq \f(n-1,3),②
①-②得3n-1an=eq \f(1,3),所以an=eq \f(1,3n)(n≥2).
由题意知a1=eq \f(1,3)符合上式,所以an=eq \f(1,3n).
考点3 由数列的递推关系求通项——综合性
考向1 累加法
(2020·安庆期末)设[x]表示不超过x的最大整数,如[-3.14]=-4,[3.14]=3.已知数列{an}满足:a1=1,an+1=an+n+1(n∈N*),则eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,a1)+\f(1,a2)+\f(1,a3)+…+\f(1,a2020)))=( )
A.1 B.2 C.3 D.4
A 解析:由an+1=an+n+1,得an-an-1=n(n≥2).
又a1=1,
所以an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=n+(n-1)+(n-2)+…+2+1=eq \f(nn+1,2),
则eq \f(1,an)=eq \f(2,nn+1)=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,n)-\f(1,n+1))).
所以eq \f(1,a1)+eq \f(1,a2)+…+eq \f(1,a2 020)=2eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,2)+\f(1,2)-\f(1,3)+…+\f(1,2 020)-\f(1,2 021)))
=2eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,2 021)))=eq \f(4 040,2 021).
所以eq \b\lc\[\rc\](\a\vs4\al\c1(\f(1,a1)+\f(1,a2)+…+\f(1,a2 020)))=eq \b\lc\[\rc\](\a\vs4\al\c1(\f(4 040,2 021)))=1.
由数列的递推关系求通项公式方法之一
已知a1,且an-an-1=f (n)时,用累加法求解.
考向2 累乘法
已知在数列{an}中,a1=1,前n项和Sn=eq \f(n+2,3)an.
(1)求a2,a3;
(2)求数列{an}的通项公式.
解:(1)由S2=eq \f(4,3)a2,得3(a1+a2)=4a2,
解得a2=3a1=3;
由S3=eq \f(5,3)a3,得3(a1+a2+a3)=5a3,
解得a3=eq \f(3,2)(a1+a2)=6.
(2)由题设知a1=1.
当n>1时,有an=Sn-Sn-1=eq \f(n+2,3)an-eq \f(n+1,3)an-1,
整理得an=eq \f(n+1,n-1)an-1.
于是a1=1,a2=eq \f(3,1)a1,a3=eq \f(4,2)a2,…,
an-1=eq \f(n,n-2)an-2,an=eq \f(n+1,n-1)an-1,
将以上n个等式两端分别相乘,
整理,得an=eq \f(nn+1,2),n≥2.
又a1=1=eq \f(1×1+1,2),也满足上式.
综上,数列{an}的通项公式an=eq \f(nn+1,2).
由数列的递推关系求通项公式方法之二
已知a1,且eq \f(an,an-1)=f (n)时,用累乘法求解.
考向3 待定系数法
设数列{an}中,a1=2,an+1=2an+3,则an=________.
5×2n-1-3 解析:设递推公式an+1=2an+3可以转化为an+1-t=2(an-t),即an+1=2an-t,解得t=-3,故an+1+3=2(an+3).令bn=an+3,则b1=a1+3=5,且eq \f(bn+1,bn)=eq \f(an+1+3,an+3)=2.所以{bn}是以5为首项,2为公比的等比数列,所以bn=5×2n-1,故an=5×2n-1-3.
由数列的递推关系求通项公式方法之三
已知a1,且an+1=qan+b,则an+1+k=q(an+k)(其中k可用待定系数法确定),可转化为{an+k}为等比数列.
考向4 取倒数法
(2020·广雅中学模拟)在数列{an}中,已知a1=2,an+1=eq \f(an,3an+1)(n∈N*),则an的表达式为( )
A.an=eq \f(2,4n-3)B.an=eq \f(2,6n-5)
C.an=eq \f(2,4n+3)D.an=eq \f(2,2n-1)
B 解析:数列{an}中,由a1=2,an+1=eq \f(an,3an+1)(n∈N*),可得eq \f(1,an+1)=3+eq \f(1,an),所以数列eq \b\lc\{\rc\}(\a\vs4\al\c1(\f(1,an)))是首项为eq \f(1,2),公差为3的等差数列,所以eq \f(1,an)=eq \f(1,2)+3(n-1)=eq \f(6n-5,2).
可得an=eq \f(2,6n-5)(n∈N*).
由数列的递推关系求通项公式方法之四
形如an+1=eq \f(Aan,Ban+C)(A,B,C为常数)的数列,可通过两边同时取倒数的方法构造新数列求解.
1.已知数列{an}满足a1=1,an+1=3an-2,则a6=( )
A.0 B.1 C.2 D.6
B 解析:因为a1=1,an+1=3an-2,所以a2=3-2=1,以此类推可得a3=3a2-2=1,a4=3a3-2=1,a5=3a4-2=1,a6=3a5-2=1.
2.已知数列{an}满足:a1=1,an+1=eq \f(2an,an+2),则a5的值为________.
eq \f(1,3) 解析:由递推公式可得:anan+1+2an+1=2an,即anan+1=2an-2an+1,据此有eq \f(1,an+1)-eq \f(1,an)=eq \f(1,2).又eq \f(1,a1)=1,故数列eq \b\lc\{\rc\}(\a\vs4\al\c1(\f(1,an)))是首项为1,公差为eq \f(1,2)的等差数列,则eq \f(1,a5)=1+eq \f(1,2)×(5-1)=3,故a5=eq \f(1,3).
3.(2020·河北联考)数列{an}满足a1=3,且对于任意的n∈N*都有an+1-an=n+2,则a39=________.
820 解析:因为an+1-an=n+2,
所以a2-a1=3,a3-a2=4,a4-a3=5,…,an-an-1=n+1(n≥2).
上面(n-1)个式子左右两边分别相加得an-a1=eq \f(n+4n-1,2)(n≥2),
即an=eq \f(n+1n+2,2)(n≥2).
当n=1时,a1=3适合上式,
所以an=eq \f(n+1n+2,2),n∈N*,
所以a39=eq \f(40×41,2)=820.
考点4 数列与函数——综合性
考向1 数列的增减性与最大值、最小值
(1)已知数列{an}的通项公式为an=n2-2λn(n∈N*),则“λ<1”是“数列{an}为递增数列”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
A 解析:若数列{an}为递增数列,则有an+1-an>0,即2n+1>2λ对任意的n∈N*都成立,于是有3>2λ,λ<eq \f(3,2).由λ<1可推得λ<eq \f(3,2),但反过来,由λ<eq \f(3,2)不能得到λ<1,因此“λ<1”是“数列{an}为递增数列”的充分不必要条件.
(2)已知数列{an}的通项an=eq \f(2n-19,2n-21),n∈N*,则数列{an}前20项中的最大项与最小项分别为________.
3,-1 解析:an=eq \f(2n-19,2n-21)=eq \f(2n-21+2,2n-21)=1+eq \f(2,2n-21),
当n≥11时,eq \f(2,2n-21)>0,且单调递减;当1≤n≤10时,eq \f(2,2n-21)<0,且单调递减.
因此数列{an}前20项中的最大项与最小项分别为第11项,第10项.
a11=3,a10=-1.
(2020·北京东城二模)已知{an}为等比数列,其前n项和为Sn,且满足a3=1,S3=3a2+1.{bn}为等差数列,其前n项和为Tn,如图__________,Tn的图象经过A,B两个点.
(1)求Sn;
(2)若存在正整数n,使得bn>Sn,求n的最小值.从图①,图②,图③中选择一个适当的条件,补充在上面问题中并作答.
解:(1)设{an}为公比为q的等比数列,
由a3=1,S3=3a2+1,得a1=2a2,即q=eq \f(a2,a1)=eq \f(1,2),a1q2=1.
所以q=eq \f(1,2),a1=4.
所以Sn=eq \f(4\b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,2n))),1-\f(1,2))=8eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,2n)))=8-23-n.
(2)由图①知T1=b1=1,T3=-3,可判断d<0,数列{bn}是递减数列.
而数列{8-23-n}递增,
因为b1<S1,所以选择①不满足“存在n,使得bn>Sn”;
由图②知:T1=b1=1,T3=6,可判断d>0,数列{bn}是递增数列;
由图③知:T1=b1=-3,T3=0,可判断d>0,数列{bn}是递增数列.
所以选择②③均可能满足“存在n,使得bn>Sn”.
第一种情况:
如果选择条件②,即T1=b1=1,T3=6,可得d=1,bn=n,
当n=1,2,3,4,5,6,7时,bn>Sn不成立.
当n=8时,b8=8,S8=8-23-8<b8.
所以使得bn>Sn成立的n的最小值为8.
第二种情况:
如果选择条件③即T1=b1=-3,T3=0,可得:d=3,bn=3n-6,
当n=1,2,3,4时,bn>Sn不成立.
当n=5时,b5=9,S5=8-23-5<b5,
所以使得bn>Sn成立的n的最小值为5.
解决数列的单调性问题常用方法
(1)用作差比较法,根据an+1-an的符号判断数列{an}是递增数列、递减数列还是常数列.
(2)用作商比较法,根据eq \f(an+1,an)(an>0或an<0)与1的大小关系进行判断.
(3)结合相应函数的图象直观判断.
考向2 数列的周期性
(2020·上杭县 5月模拟)设数列{an}满足:a1=2,an+1=1-eq \f(1,an),记数列{an}的前n项之积为Pn,则P2 021( )
A.-eq \f(1,2) B.eq \f(1,2) C.1 D.-1
D 解析:a1=2,an+1=1-eq \f(1,an),得a2=eq \f(1,2),a3=-1,a4=2,此时数列的项开始重复出现,呈现周期性,周期为3.
且P3=-1,2021=3×673+2,
所以P2 021=(-1)673×a1a2=-1.
解决数列周期性问题的方法
先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值.
考向3 新定义问题
对于数列{xn},若对任意n∈N*,都有eq \f(xn+xn+2,2)<xn+1成立,则称数列{xn}为“减差数列”.设bn=2t-eq \f(tn-1,2n-1),若数列b3,b4,b5,…是“减差数列”,则实数t的取值范围是( )
A.(-1,+∞)B.(-∞,-1]
C.(1,+∞)D.(-∞,1]
C 解析:由数列b3,b4,b5,…是“减差数列”,
得eq \f(bn+bn+2,2)<bn+1(n≥3),
即t-eq \f(tn-1,2n)+t-eq \f(tn+2-1,2n+2)<2t-eq \f(tn+1-1,2n),
即eq \f(tn-1,2n)+eq \f(tn+2-1,2n+2)>eq \f(tn+1-1,2n),
化简得t(n-2)>1.
当n≥3时,若t(n-2)>1恒成立,则t>eq \f(1,n-2)恒成立,
又当n≥3时,eq \f(1,n-2)的最大值为1,
则t的取值范围是(1,+∞).
解决数列的新定义问题的要点
(1)准确转化:解决数列新定义问题时,一定要读懂新定义的本质含义,将题目所给定义转化成题目要求的形式,切忌同已有概念或定义相混淆.
(2)方法选取:对于数列新定义问题,搞清定义是关键,仔细认真地从前几项(特殊处、简单处)体会题意,从而找到恰当的解决方法.
1.观察数列1,ln 2,sin 3,4,ln 5,sin 6,7,ln 8,sin 9,…,则该数列的第11项是( )
A.1111B.11
C.ln 11D.sin 11
C 解析:由数列得出规律,按照1,ln 2,sin 3,…,是按正整数的顺序排列,且以3为循环节,
由11÷3=3余2,所以该数列的第11项为ln 11.
2.已知an=eq \f(n-1,n+1),那么数列{an}是( )
A.递减数列B.递增数列
C.常数列D.摆动数列
B 解析:an=1-eq \f(2,n+1),将an看作关于n的函数,n∈N*,易知数列{an}是递增数列.
3.若数列{an}的前n项和Sn=n2-10n(n∈N*),则数列{nan}中数值最小的项是( )
A.第2项B.第3项
C.第4项D.第5项
B 解析:因为Sn=n2-10n,
所以当n≥2时,an=Sn-Sn-1=2n-11.
当n=1时,a1=S1=-9也适合上式,
所以an=2n-11(n∈N*).
记f (n)=nan=n(2n-11)=2n2-11n,
此函数图象的对称轴为直线n=eq \f(11,4),但n∈N*,
所以当n=3时,f (n)取最小值.
所以数列{nan}中数值最小的项是第3项.
已知数列{an}中,a1=3,且n(n+1)(an-an+1)=2.
(1)求数列{an}的通项公式;
(2)设bn=eq \f(a1·a2·…·an,n+1·2n),求数列{bn}的前n项和Sn.
[四字程序]
思路参考:(1)累加法;(2)错位相减法.
解:(1)由题意知,an-an+1=eq \f(2,nn+1)=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,n)-\f(1,n+1))),
所以n≥2时,an-1-an=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,n-1)-\f(1,n))),
an-2-an-1=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,n-2)-\f(1,n-1))),
…,
a1-a2=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,1)-\f(1,2))),
以上(n-1)个式子左右两边分别相加得
a1-an=2eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(1,n))).
又a1=3,所以an=1+eq \f(2,n)(n≥2).
又a1=3符合上式,故an=1+eq \f(2,n)(n∈N*).
(2)由(1)知,an=1+eq \f(2,n)=eq \f(n+2,n),
所以a1a2…an=eq \f(3,1)×eq \f(4,2)×…×eq \f(n+1,n-1)×eq \f(n+2,n)=eq \f(n+1n+2,2),
所以bn=eq \f(a1·a2·…·an,n+1·2n)=eq \f(n+2,2n+1),
所以Sn=eq \f(3,22)+eq \f(4,23)+eq \f(5,24)+…+eq \f(n+1,2n)+eq \f(n+2,2n+1),
eq \f(1,2)Sn=eq \f(3,23)+eq \f(4,24)+eq \f(5,25)+…+eq \f(n+1,2n+1)+eq \f(n+2,2n+2),
两式相减得eq \f(1,2)Sn=eq \f(3,22)+eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,23)+\f(1,24)+…+\f(1,2n+1)))-eq \f(n+2,2n+2)=eq \f(3,4)+eq \f(\f(1,23)\b\lc\[\rc\](\a\vs4\al\c1(1-\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))\s\up10(n-1))),1-\f(1,2))-eq \f(n+2,2n+2)=1-eq \f(1,2n+1)-eq \f(n+2,2n+2)=1-eq \f(n+4,2n+2),故Sn=2-eq \f(n+4,2n+1).
思路参考:(1)选代法;(2)裂项相消法.
解:(1)由题意知,an-an+1=eq \f(2,nn+1)=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,n)-\f(1,n+1))),
所以an+1-eq \f(2,n+1)=an-eq \f(2,n),
所以an-eq \f(2,n)=an-1-eq \f(2,n-1)=…=a1-eq \f(2,1)=3-2=1,
所以an=1+eq \f(2,n).
(2)由(1)知an=1+eq \f(2,n)=eq \f(n+2,n),
所以a1·a2·…·an=eq \f(3,1)×eq \f(4,2)×…×eq \f(n+1,n-1)×eq \f(n+2,n)=eq \f(n+1n+2,2),
所以bn=eq \f(a1·a2·…·an,n+1·2n)=eq \f(n+2,2n+1)=eq \f(n+3,2n)-eq \f(n+4,2n+1),
所以Sn=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,21)-\f(5,22)))+eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,22)-\f(6,23)))+…+eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(n+3,2n)-\f(n+4,2n+1)))=2-eq \f(n+4,2n+1).
1.本题考查数列求通项公式与前n项和问题,解法灵活多变,基本解题策略是借助于数列的递推关系求通项公式,利用裂项相消法或错位相减法求数列的前n项和,对于此类问题要注意观察条件的特点,合理转化.
2.基于课程标准,解答本题一般需要学生熟练掌握数学推理能力、运算求解能力和表达能力,体现了逻辑推理、数学运算的核心素养.
已知数列{an}中,a1=1,an+1=3an+2,求数列{an}的通项公式.
解:(方法一)an+1=3an+2,即an+1+1=3(an+1),
即eq \f(an+1+1,an+1)=3,
所以eq \f(a2+1,a1+1)=3,eq \f(a3+1,a2+1)=3,eq \f(a4+1,a3+1)=3,…,eq \f(an+1+1,an+1)=3.
将这些等式两边分别相乘得eq \f(an+1+1,a1+1)=3n.
因为a1=1,所以eq \f(an+1+1,1+1)=3n,
即an+1=2×3n-1(n≥1),
所以an=2×3n-1-1(n≥2).
又a1=1也满足上式,
故数列{an}的一个通项公式为an=2×3n-1-1.
(方法二)an+1=3an+2,
即an+1+1=3(an+1)=32(an-1+1)=33(an-2+1)
=…=3n(a1+1)=2×3n(n≥1),
所以an=2×3n-1-1(n≥2).
又a1=1也满足上式,
故数列{an}的一个通项公式为an=2×3n-1-1.
课程标准
命题解读
1.了解数列的概念和表示方法(列表、图象、通项公式),了解数列是一种特殊函数.
2.理解等差数列的概念和通项公式的意义.
3.探索并掌握等差数列的前n项和公式,理解等差数列的通项公式与前n项和公式的关系.
4.能在具体的问题情境中,发现数列的等差关系,并解决相应的问题。体会等差数列与一元一次函数的关系.
5.理解等比数列的概念和通项公式的意义.
6.探索并掌握等比数列的前n项和公式,理解等比数列的通项公式与前n项和公式的关系.
7.能在具体的问题情境中,发现数列的等比关系,并解决相应的问题。体会等比数列与指数函数的关系.
考查形式:一般为一个选择题和一个填空题或一个解答题
考查内容:数列的概念及表示方法、等差数列、等比数列的定义、性质、通项公式与前n项和公式、数列求和及其应用.
备考策略:(1)熟练应用等差数列、等比数列的通项公式与前n项和公式求值.
(2)重视数列与函数关系的研究,注意函数性质在数列中的应用.
(3)加强数列求和问题的训练.
核心素养:数学抽象、直观想象、数学运算.
数列
内容
定义
按照确定的顺序排列的一列数称为数列,
数列中的每一个数叫做这个数列的项,数列的第n项用an表示
表示
a1,a2,a3,…,an,…,简记为{an}
函数观点
an=f (n),n∈N*
分类标准
名称
含义
按项的个数
有穷数列
项数有限的数列
无穷数列
项数无限的数列
按项的变化趋势
递增数列
从第2项起,每一项都大于它的前一项的数列⇔an
从第2项起,每一项都小于它的前一项的数列⇔an>an+1
常数列
各项都相等的数列⇔an=an+1
摆动数列
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列
数列的形式
意义
特点
通项公式
用公式an=f (n),n∈N*给出数列
可以求任意项
递推公式
给出首项,相邻两项或多项之间的关系
需依次求各项
读
想
算
思
求通项公式与前n项和
1.求通项公式的方法;
2.怎样对已知条件变形?
变形已知条件,求通项公式,求和
转化与化归
数列{an}中,a1=3,n(n+1)·(an-an+1)=2
1.累加法与错位相减法;
2.构造法与裂项相消法
1.由an-an+1=eq \f(2,nn+1)=2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,n)-\f(1,n+1))),求an;
2.由bn=eq \f(n+2,2n+1),求Sn
1.累加法与构造法求数列的通项公式;
2.错位相减法与裂项相消法求和
高考数学一轮复习教案 第5章_第1节_数列的概念与简单表示法(含答案解析): 这是一份高考数学一轮复习教案 第5章_第1节_数列的概念与简单表示法(含答案解析),共9页。
高中数学高考第1节 数列的概念与简单表示法 教案: 这是一份高中数学高考第1节 数列的概念与简单表示法 教案,共11页。
高中数学2.1 数列的概念与简单表示法第1课时教案: 这是一份高中数学2.1 数列的概念与简单表示法第1课时教案,共3页。












