












2020-2021学年第二十八章 锐角三角函数28.2 解直角三角形及其应用一等奖ppt课件
展开学习目标1. 知道仰角、俯角的概念.2. 会根据仰角、俯角的概念结合直角三角形的知识解决实际问题.
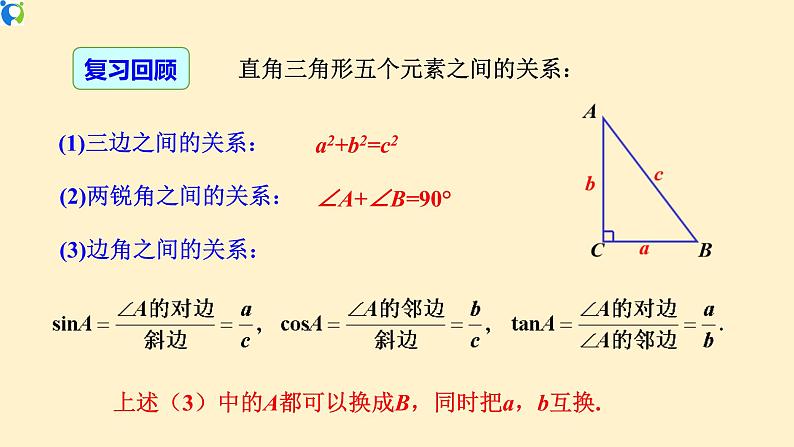
(2)两锐角之间的关系:
(3)边角之间的关系:
(1)三边之间的关系:
上述(3)中的A都可以换成B,同时把a,b互换.
直角三角形五个元素之间的关系:
平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
三种:重叠、向上和向下
利用仰角、俯角解直角三角形
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
例:热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
Rt△ABD中,a =30°,AD=120,所以利用解直角三角形的知识求出BD的长度;类似地可以求出CD的长度,进而求出BC的长度,即求出这栋楼的高度.
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°.
解:如图,a = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
1. 如图,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为150米,且点A、D、B在同一直线上,则建筑物A、B间的距离为( ) A. 150 米 B. 180 米 C. 200 米 D. 220 米
3. 如图,在高度为10米的平台CD上测得一高层建筑物AB的顶端A的仰角为60°,底端B的俯角为30°,则高层建筑物的高AB= 米.
4. 建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
解:在等腰Rt△BCD中,∠ACD=90°,
∴AB=AC-BC=55.1-40=15.1 (m).
5. 如图,直升飞机在高为200米的大楼AB上方P点处, 从大楼的顶部和底部测得飞机的仰角为30°和45°, 求飞机的高度PO .
解:如图,过点P作PC⊥BA的延长线于点C.
则∠PBO=∠CPB=45°,∠CPA=30°,
解含有仰角、俯角问题的方法:(1)仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的,可巧记为“上仰下俯”; (2)视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度;(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
1. 如图①,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=______米.2. 如图②,两建筑物AB和CD的水平距离为30米,从A点测得 D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.
3. 为测量松树AB的高度,一个人站在距松树15米的E 处,测得仰角∠ACD=52°,已知人的高度是1.72米,则树高 (精确到0.1米).
4. 如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cs37 °≈0.6,tan 37°≈0.75)
在Rt△POB中∠PBO=45°,
在Rt△POA中,∠PAB=37°,
解:作PO⊥AB交AB的延长线于点O.
故飞机的高度为1200米.
如图,小明想测量塔AB的高度. 他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m. 那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?
分析:由图可知,塔高AB可以分为两部分,上部分AB′可以在Rt△AD′B′和Rt△AC′B′中利用仰角的正切值求出,B′B与D′D相等.
解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°,D′C′=50m. ∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50m , 设AB′=x m.
1.(10分)(2021•新疆20/23)如图,楼顶上有一个广告牌AB,从与楼BC相距15m的D处观测广告牌顶部A的仰角为37°,观测广告牌底部B的仰角为30°,求广告牌AB的高度.(结果保留小数点后一位,参考数据:sin37°≈0.60,cs37°≈0.80,tan37°≈0.75, ≈1.41, ≈1.73)
【考点】解直角三角形的应用﹣仰角俯角问题. 【分析】利用CD及正切函数的定义求得BC,AC长,把这两条线段相减即为AB长.
2.(8分)(2021•西藏25/27)如图,为了测量某建筑物CD的高度,在地面上取A,B两点,使A、B、D三点在同一条直线上,拉姆同学在点A处测得该建筑物顶部C的仰角为30°,小明同学在点B处测得该建筑物顶部C的仰角为45°,且AB=10 m.求建筑物CD的高度.(拉姆和小明同学的身高忽略不计.结果精确到0.1 m, )
3.(8分)(2020•吉林20/26)如图,某班数学小组测量塔的高度,在与塔底部B相距35 m的C处,用高1.5 m的测角仪CD测得该塔顶端A的仰角∠EDA为36°.求塔AB的高度(结果精确到1 m).(参考数据:sin36°=0.59,cs36°=0.81,tan36°=0.73)
利用仰俯角解直角三角形
运用解直角三角形解决仰角、俯角问题
在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
仰角、俯角问题的常见基本模型:
湘教版九年级上册4.4 解直接三角形的应用一等奖课件ppt: 这是一份湘教版九年级上册4.4 解直接三角形的应用一等奖课件ppt,共16页。PPT课件主要包含了观察与思考,俯角的概念,水平线,β60°,BCDC40m,练一练,解得x400,解直角三角形的应用等内容,欢迎下载使用。
初中数学湘教版九年级上册4.4 解直接三角形的应用完美版ppt课件: 这是一份初中数学湘教版九年级上册4.4 解直接三角形的应用完美版ppt课件,共16页。PPT课件主要包含了观察与思考,俯角的概念,水平线,铅垂线,a30°,β60°,BCDC40m,练一练,解得x400,答塔高约为45米等内容,欢迎下载使用。
初中数学北师大版九年级下册5 三角函数的应用一等奖习题课件ppt: 这是一份初中数学北师大版九年级下册5 三角函数的应用一等奖习题课件ppt,文件包含152仰角俯角问题课件pptx、第一章直角三角形的边角关系5三角函数的应用习题152课件pptx、152三角函数的应用2教案doc等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。














