





2020-2021学年第八章 机械能守恒定律综合与测试教学ppt课件
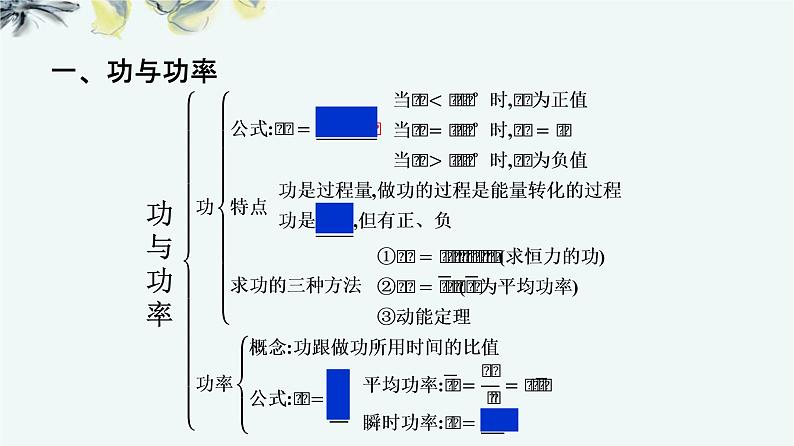
展开本章知识可分为三个组成部分。第一部分:功与功率;第二部分:机械能;第三部分:功能关系。
一、变力做功的求解方法1.微元法:将物体的位移分割成许多小段,因小段很小,每一小段上作用在物体上的力可以视为恒力,这样就将变力做功转化为在无数个无穷小的位移上的恒力所做功的代数和,此法在中学阶段常应用于求解大小不变、方向改变的变力做功问题。2.等效转换法:在某些情况下,通过等效转换可以将变力做功转换成恒力做功,然后可以用公式W=Flcs α求解。
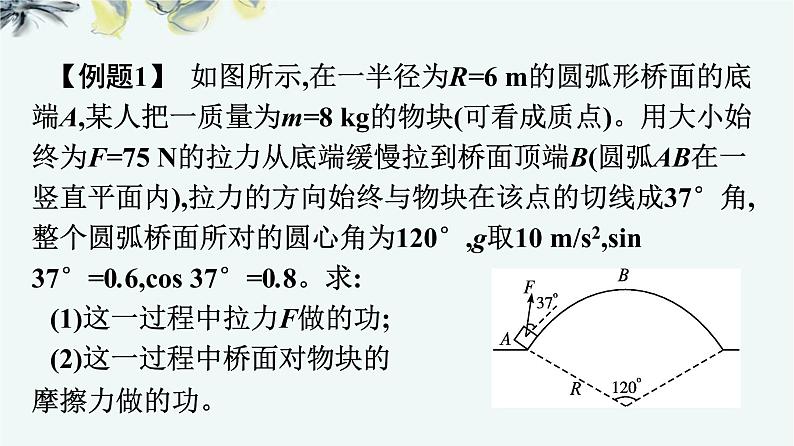
【例题1】 如图所示,在一半径为R=6 m的圆弧形桥面的底端A,某人把一质量为m=8 kg的物块(可看成质点)。用大小始终为F=75 N的拉力从底端缓慢拉到桥面顶端B(圆弧AB在一竖直平面内),拉力的方向始终与物块在该点的切线成37°角,整个圆弧桥面所对的圆心角为120°,g取10 m/s2,sin 37°=0.6,cs 37°=0.8。求:(1)这一过程中拉力F做的功;(2)这一过程中桥面对物块的摩擦力做的功。
(2)因为重力G做的功WG=-mgR(1-cs 60°)=-240 J,而因物块在拉力F作用下缓慢移动,动能不变,由动能定理知WF+WG+Wf=0所以Wf=-WF-WG=-376.8 J+240 J=-136.8 J。答案:(1)376.8 J (2)-136.8 J科学思维动能定理既适用于直线运动,也适用于曲线运动,既适用于求恒力做功,也适用于求变力做功,因此利用动能定理求变力做功也是非常方便的。
【变式训练1】 如图所示,轻弹簧一端与竖直墙壁连接,另一端与一质量为m的木块连接,放在光滑的水平面上,弹簧的劲度系数为k,弹簧处于自然状态,用水平力F缓慢拉木块,使木块前进x0,求这一过程中拉力对木块做了多少功。
二、动能定理解决多过程问题1.分段应用动能定理时,将复杂的过程分割成一个个子过程,对每个子过程的做功情况和初、末动能进行分析,然后针对每个子过程应用动能定理列式,然后联立求解。2.全程应用动能定理时,分析整个过程中出现过的各力的做功情况,分析每个力的做功,确定整个过程中合外力做的总功,然后确定整个过程的初、末动能,针对整个过程利用动能定理列式求解。3.当题目不涉及中间量时,选择全程应用动能定理更简单,更方便。
【例题2】 如图所示,竖直平面内的 圆弧形光滑管道半径略大于小球半径,管道中心线到圆心的距离为R,A端与圆心O等高,AD为水平面,B点在O的正下方,小球自A点正上方由静止释放,自由下落至A点时进入管道,从上端口飞出后落在C点,当小球到达B点时,管壁对小球的弹力大小是小球重力大小的9倍。求:(1)释放点距A点的竖直高度;(2)落点C与A点的水平距离。
解析:(1)设小球到达B点的速度为v1,因为到达B点时管壁对小球的弹力大小是小球重力大小的9倍,
由①②得h=3R。③
(2)设小球到达圆弧最高点的速度为v2,落点C与A点的水平距离为x从B到最高点的过程中,由动能定理得
科学思维动能定理一般应用于单个物体,既适用于各个力同时作用在物体上,也适用于不同的力分阶段作用在物体上,凡涉及力对物体做功过程中动能的变化问题都可以使用。
【变式训练2】 如图所示,ABCD为一竖直平面内的轨道,其中BC水平,A点比BC高出10 m,BC长1 m,AB和CD轨道光滑。一质量为1 kg的物体,从A点以4 m/s的速度开始运动,经过BC后滑到高出C点10.3 m的D点速度为0。g取10 m/s2。求:(1)物体与BC轨道间的动摩擦因数;(2)物体第5次经过B点时的速度;(3)物体最后停止的位置(距B点多少米)。
(3)分析整个过程,由动能定理得
解得s=21.6 m。所以物体在轨道上来回运动了10次后,还有1.6 m,故距B点的距离为2 m-1.6 m=0.4 m。答案:(1)0.5(2)13.3 m/s(3)距B点0.4 m
三、多物体的机械能守恒问题1.首先分析多个物体组成的系统所受的外力是否只有重力或弹力做功,内力是否造成了机械能与其他形式能的转化,从而判断系统机械能是否守恒。2.若系统机械能守恒,则机械能从一个物体转移到另一个物体,ΔE1=-ΔE2,一个物体机械能增加,则一定有另一个物体机械能减少。
【例题3】 如图所示,质量分别为3 kg和5 kg的物体A、B,用轻绳连接跨在一个定滑轮两侧,轻绳正好拉直,且A物体底面与地接触,B物体距地面0.8 m。g取10 m/s2。(1)放开B物体,当B物体着地时,求A物体的速度;(2)B物体着地后A物体还能上升多高?
解析:(1)方法一:由E1=E2。对A、B组成的系统,当B下落时系统机械能守恒,以地面为参考平面,则
(2)当B落地后,A以2 m/s的速度竖直上抛,则A上升的高度,由机械能守恒可得
答案:(1)2 m/s (2)0.2 m
科学思维多物体的机械能守恒问题分析技巧1.对多物体,一般用“转化法”和“转移法”来判断其机械能是否守恒。2.注意寻找用绳或杆相连接的物体间的速度关系和位移关系。3.列机械能守恒方程时,可选用ΔEk=-ΔEp的形式。
【变式训练3】 下图是一个横截面为半圆、半径为R的光滑柱面。一根不可伸长的细线两端分别系着物体A、B,且mA=2mB。由图示位置从静止开始释放物体A,当物体B到达圆柱顶点时,求细线的拉力对物体B所做的功。解析:由于圆柱面是光滑的,故系统的机械能守恒。系统重力势能的减少量
由ΔEp减=ΔEk增,得
四、功能关系的理解和应用1.功能关系功是能量转化的量度。不同形式的能量之间的转化是通过做功实现的,做功的过程就是各种形式的能量之间转化的过程,而且做了多少功,就有多少能量发生转化。
2.几种常见的功能关系
【例题4】 (多选)滑沙是人们喜爱的游乐活动,下图是滑沙场地的一段斜面,其倾角为30°,设参加活动的人和滑车总质量为m,人和滑车从距底端高为h处的顶端A沿滑道由静止开始匀加速下滑,加速度为0.4g,人和滑车可视为质点,则从顶端向下滑到底端B的过程中,下列说法正确的是( )A.人和滑车减少的重力势能全部转化为动能B.人和滑车获得的动能为0.8mghC.整个下滑过程中人和滑车减少的机械能为0.2mghD.人和滑车克服摩擦力做功为0.6mgh
解析:沿斜面的方向有ma=mgsin 30°-Ff,所以Ff=0.1mg,人和滑车减少的重力势能转化为动能和内能,故A错误;人和滑车下滑的过程中重力和摩擦力做功,获得的动能为Ek=(mgsin
少的机械能为ΔE=mgh-Ek=mgh-0.8mgh=0.2mgh,故C正确;整个下滑过程中克服摩擦力做功等于人和滑车减少的机械能,所以人和滑车克服摩擦力做功为0.2mgh,故D错误。答案:BC
科学思维功能关系的选用原则1.若只涉及动能的变化,则用动能定理分析。2.若只涉及重力势能的变化,则用重力做功与重力势能变化的关系分析。
【变式训练4】 在奥运比赛项目中,高台跳水是我国运动员的强项。质量为60 kg的跳水运动员进入水中后受到水的阻力做竖直向下的减速运动,设水对他的阻力大小恒为2 600 N,那么在他减速下降2 m的过程中,下列说法正确的是(g取10 m/s2)( )A.他的动能减少了5 200 JB.他的重力势能减少了1 200 JC.他的机械能减少了4 000 JD.他的机械能保持不变
解析:在运动员减速下降2 m的过程中,运动员受重力和阻力,由动能定理得(mg-F)h=ΔEk,解得ΔEk=-4 000 J,A错误;他的重力势能减少了mgh=1 200 J,B正确;除了重力、弹力之外的力做的功等于机械能的变化,故他的机械能减少了Fh=5 200 J,C、D错误。答案:B
2021学年第六章 圆周运动综合与测试教学ppt课件: 这是一份2021学年第六章 圆周运动综合与测试教学ppt课件,共60页。PPT课件主要包含了学习目标,重点探究,1最低点,2最高点,3临界状态,答案2ms,答案15N,易错提醒,随堂演练,图10等内容,欢迎下载使用。
高中物理人教版 (2019)必修 第二册第八章 机械能守恒定律综合与测试教学课件ppt: 这是一份高中物理人教版 (2019)必修 第二册第八章 机械能守恒定律综合与测试教学课件ppt,共37页。PPT课件主要包含了知识点归纳与概括,重力势能,弹性势能,本章知识结构图,据动能定理有,解二由动能定理得,重点剖析,求解公式等内容,欢迎下载使用。
高中物理人教版 (2019)必修 第二册第七章 万有引力与宇宙航行综合与测试教学ppt课件: 这是一份高中物理人教版 (2019)必修 第二册第七章 万有引力与宇宙航行综合与测试教学ppt课件,共37页。PPT课件主要包含了宇宙航行,向心加速度,动力学规律,卫星变轨的实质,答案D,答案80∶1等内容,欢迎下载使用。













