初中人教版27.2.1 相似三角形的判定图文课件ppt

这是一份初中人教版27.2.1 相似三角形的判定图文课件ppt，共19页。PPT课件主要包含了学习目标，判定三角形相似的方法，知识回顾，∴△ABC∽△DEF，∠A∠D，∴△ADE∽△ABC，测量会存在误差，判定定理３，符号语言，得出结论等内容，欢迎下载使用。

1.知道两角分别相等的两个三角形相似；知道斜边、直角边成比例的两个直角三角形相似. 2.能证明结论“斜边、直角边成比例的两个直角三角形相似”. 3.能灵活选择适当的方法证明两个三角形相似.
（2）图２∵DE∥BC
（1）图１∵∠A=∠D, ∠B= ∠E, ∠C= ∠F
观察：观察下列两副三角板 ，其中有同样两个锐角（ 30度与60度，或45度 与45度的两个三角尺大小不同，但它们看起来相似吗 ？ 　
猜想：两角分别相等的两个三角形相似．
四人小组合作:同学们把课前画好的有两个锐角度数分别为40度 60度的三角形进行测量并计算各对应边的比值，发现了什么？ 
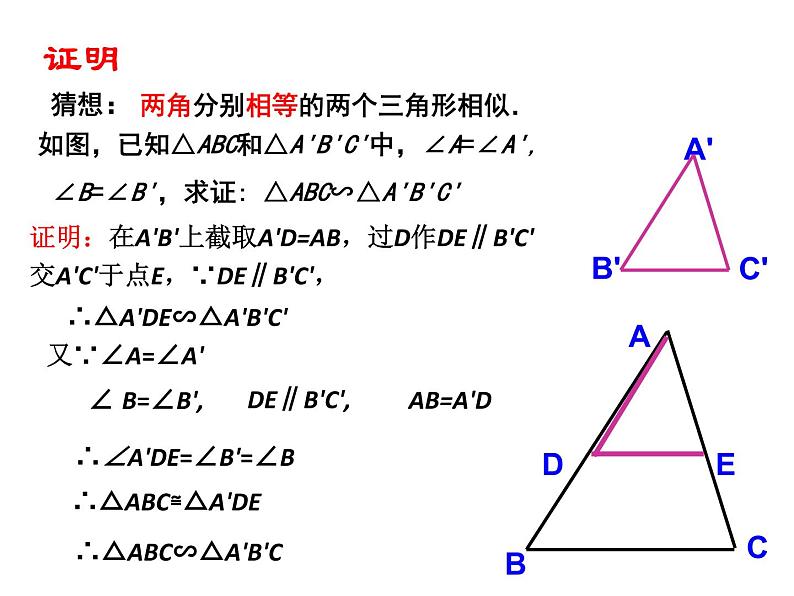
如图，已知△ABC和△A'B'C'中，∠A=∠A', ∠B=∠B'，求证: △ABC∽△A'B'C'
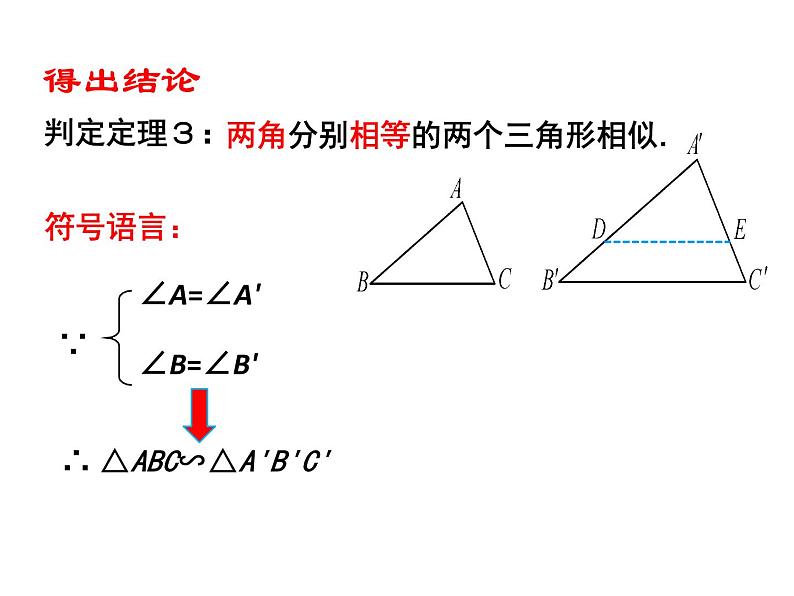
两角分别相等的两个三角形相似．
∴△A'DE∽△A'B'C'
证明：在A'B'上截取A'D=AB，过D作DE∥B'C'交A'C'于点E，∵DE∥B'C'，
∴∠A'DE=∠B'=∠B
∴△ABC≌△A'DE
∴△ABC∽△A'B'C
∴ △ABC∽△A'B'C'
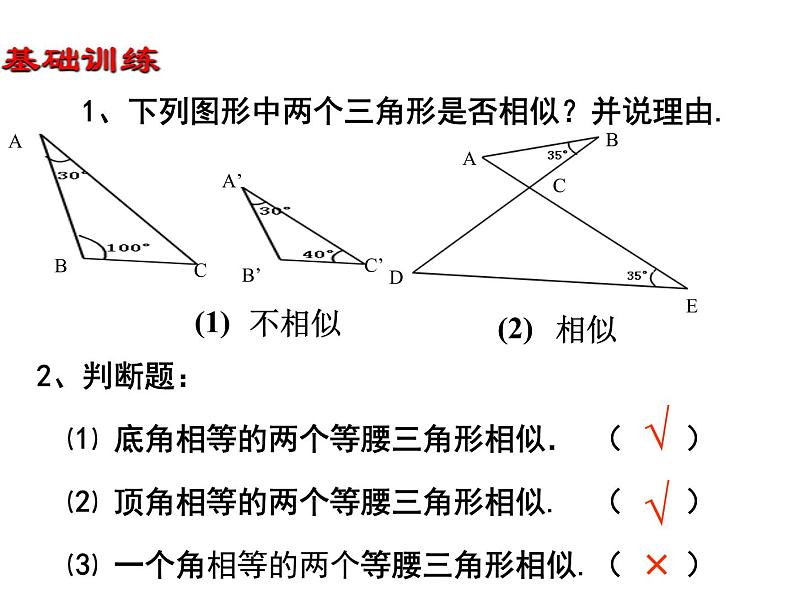
1、下列图形中两个三角形是否相似？并说理由.
2、判断题： ⑴ 底角相等的两个等腰三角形相似． （　　） ⑵ 顶角相等的两个等腰三角形相似. （ ） ⑶ 一个角相等的两个等腰三角形相似.（ ）
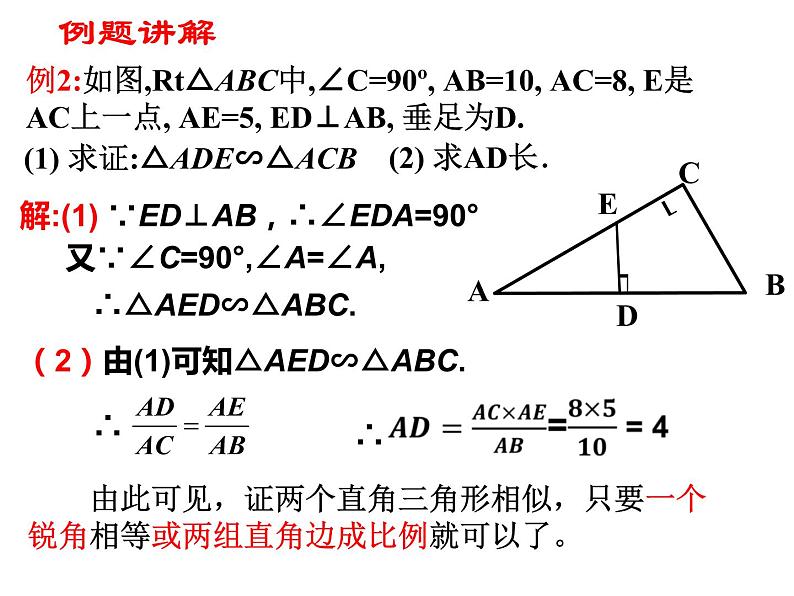
例2:如图,Rt△ABC中,∠C=90º, AB=10, AC=8, E是AC上一点, AE=5, ED⊥AB, 垂足为D.
由此可见，证两个直角三角形相似，只要一个锐角相等或两组直角边成比例就可以了。
(1) 求证:△ADE∽△ACB
解:(1) ∵ED⊥AB，∴∠EDA=90°
又∵∠C=90°,∠A=∠A,
∴△AED∽△ABC.
（2）由(1)可知△AED∽△ABC.
１.底角相等的两个等腰三角形是否相似？顶角相等的两个等腰三角形呢？证明你的结论.
解：（1）相似（2）相似都符合两个角对应相等的两个三角形相似.
２、如图，Rt△ABC中，CD是斜边上的高，（1）△ACD与△ABC相似吗？
结论:直角三角形斜边上的高分成的两个三角形与原三角形
（2）△BCD与△BAC相似吗？
（3）△ACD与△CBD相似吗？
2、如图，利用标杆BE测量建筑物高度，如果标杆BE高1.2m，测得AB＝1.6m，BC＝12.4m，楼高CD是多少？
我们知道，两个直角三角形全等可以用“HL”来判定，那么满足斜边和一条直角边成比例的两个直角三角形相似吗？
如图，在Rt△ABC和Rt△A'B'C'中，∠C=90°，∠C'=90°， ， 求证Rt△ABC∽ Rt△A'B'C'.
分析：要证Rt△ABC∽ Rt△A'B'C'.
则AB=kA'B'，AC=kA'C'
Rt△ABC∽ Rt△A'B'C'.
∴R △ABC ∽ R△A'B'C'
斜边和一条直角边成比例的两个直角三角形相似．
如果Rt∆ABC的两条直角边分别为3和4, 那么以3k和4k（k是正整数） 为直角边的直角三角形 一定与Rt∆ABC相似吗？ 为什么 ？
填空:如图,当满足＿＿＿＿时， △ABC和△ADE 相似.
方法２：∠ADE=∠B或∠AED=∠C　　
作业: 1.必做题 P42第2 题中(2) 2.选做题 P43第7题