九年级下册3. 圆周角精品教学ppt课件

这是一份九年级下册3. 圆周角精品教学ppt课件，共30页。PPT课件主要包含了什么是弦，圆周角，探究1圆周角的概念，圆周角与其他角的区别，探究3圆周角定理，量一量，∵OAOC，作直径CD，∠1∠4，∠2∠7等内容，欢迎下载使用。

连接圆上任意两点的线段叫做弦.
什么是弧？什么是等弧？
圆上任意两点间的部分叫作圆弧，简称弧。
在同圆或等圆中，能够互相重合的弧叫做等弧.
你知道∠ACB是什么角吗？
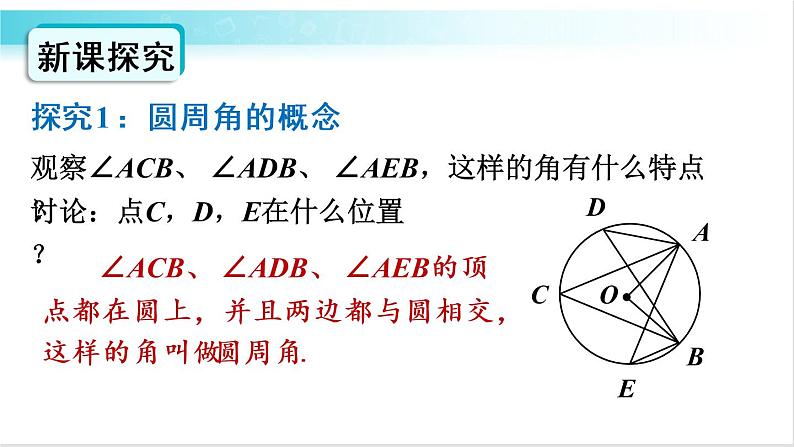
观察∠ACB、 ∠ADB、 ∠AEB，这样的角有什么特点？
讨论：点C，D，E在什么位置？
∠ACB、 ∠ADB、 ∠AEB的顶点都在圆上，并且两边都与圆相交，这样的角叫做圆周角.
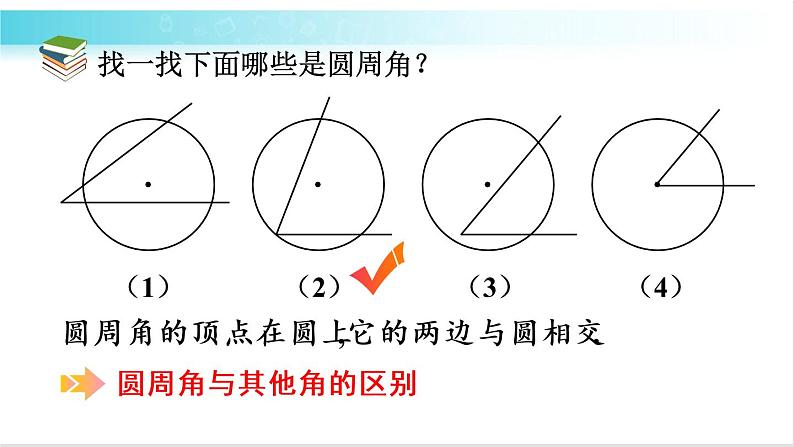
找一找下面哪些是圆周角？
圆周角的顶点在圆上,它的两边与圆相交.
探究2：半圆或直径所对的圆周角都相等，都等于90°
线段AB是⊙O的直径 ，点C是⊙O上的任意一点（除点A、B外），那么，∠ACB 就是直径AB所对的圆周角.想想看，∠ACB会是怎样的角？
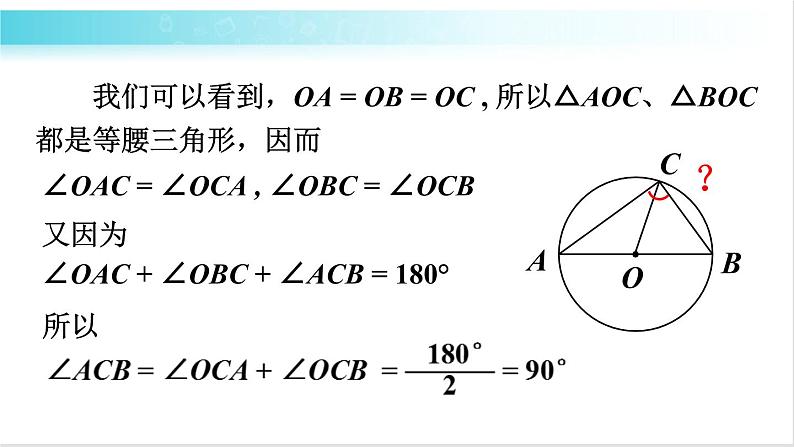
我们可以看到，OA = OB = OC , 所以△AOC、△BOC 都是等腰三角形，因而
∠OAC = ∠OCA , ∠OBC = ∠OCB
又因为∠OAC + ∠OBC + ∠ACB = 180°
因此，不管点C在⊙O上何处（除点A、B外），∠ACB总等于90°，即：
半圆或直径所对的圆周角都相等，都等于90°（直角）.
∠ADB ∠ACB
变动点C在圆周上的位置，你发现其中有什么规律吗?
可以发现圆周角的度数没有变化
∠ACB ∠AOB
我们发现圆周角的度数恰好为同弧所对的圆心角的度数的一半.
在圆上任取一个圆周角，观察圆心角顶点与圆周角的位置关系有几种情况？
共有三种情况：（1）圆心在圆周角的一边上; （2）圆心在圆周角的内部; （3）圆心在圆周角的外部.
分别就这三种情况证明这一猜想.
已知：在⊙O的一条弦 , 所对的圆周角是∠ACB， 所对的圆心角是∠AOB.
（1）圆心在∠ACB的边CB上.
∴ ∠OAC = ∠ACB ，
∵ ∠AOB 是△OAC的外角，
∴ ∠AOB = ∠ACB +∠OAC = 2∠ACB ，
（3）圆心在∠ACB的外部.
∴ ∠1 = ∠AOD ，
∴ ∠ACB = ∠1－∠2= （∠AOD －∠BOD）
∠2 = ∠BOD ，
= ∠AOB .
由此我们可以得到： 圆周角定理 在同圆或等圆中,同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
探究4：外接圆、内接多边形
由圆周角定理，可以得到以下推论:
推论1：90°的圆周角所对的弦是直径.
如果一个圆经过一个多边形的各个顶点，这个圆就叫做这个多边形的外接圆，这个多边形叫做这个圆的内接多边形.
推论2：圆内接四边形的对角互补.
如右图 ∠BAD + ∠BCD = 180°
∠ABC + ∠ADC = 180°
（1）∵同弧对的圆周角相等， ∴∠ x = 60°.
（2）连接BF， ∵同弧所对的圆周角相等， ∴∠ABF = ∠D = 20°， ∠FBC = ∠E = 30°， ∴∠ x = ∠ABF + ∠FBC= 50°.
1．试找出图中所有相等的圆周角.
2.在圆中，一条弧所对的圆心角和圆周角分别为(2x +100 )°和(5x－30)°，求这条弧所对的圆心角和圆周角的大小.
(2x+100)°= 2( 5x－30) °
∴(2x+100) °= 140° ， ( 5x－30) °=70°.
故这条弧所对的圆心角为140°，圆周角为70°.
3.使用曲尺检验工件的凹面，成半圆时为合格.如图所示的三种情况中，哪种是合格的?哪种是不合格的?为什么?
第三种合格,另外两种不合格.
∵ 90°的圆周角所对的弦是直径，
∴若要合格，曲尺顶点应在圆周上，曲尺两边应与凹面的两个端点接触，
∴只有第三种情况符合.
证明：∵OA ⊥ OB， ∴∠AOB = 90°， ∴∠C = ∠D = 45°， ∵AC ⊥ BD， ∴∠DEC = 90°， ∴∠DAE = 45°， ∴∠C = ∠DAE. ∴AD∥BC
顶点在圆上，两边与圆相交的角叫做圆周角.
圆周角定理 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.从课后习题中选取；2.完成练习册本课时的习题.