专题9.1 中心对称图形-平行四边形（基础篇）专项练习-【挑战满分】2021-2022学年八年级数学下册阶段性复习精选精练（苏科版）

这是一份专题9.1 中心对称图形-平行四边形（基础篇）专项练习-【挑战满分】2021-2022学年八年级数学下册阶段性复习精选精练（苏科版），共27页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
专题9.1 中心对称图形-平行四边形（基础篇）专项练习
一、单选题
1．下列标志既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
2．如图，在▱ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于 （　 　）

A．1cm B．2cm C．3cm D．4cm
3．如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一直线上，则三角板ABC旋转的度数是（ 　）

A．60° B．90° C．120° D．150°
4．不考虑颜色，对如图的对称性表述，正确的是( )

A．轴对称图形
B．中心对称图形
C．既是轴对称图形又是中心对称图形
D．既不是轴对称图形又不是中心对称图形
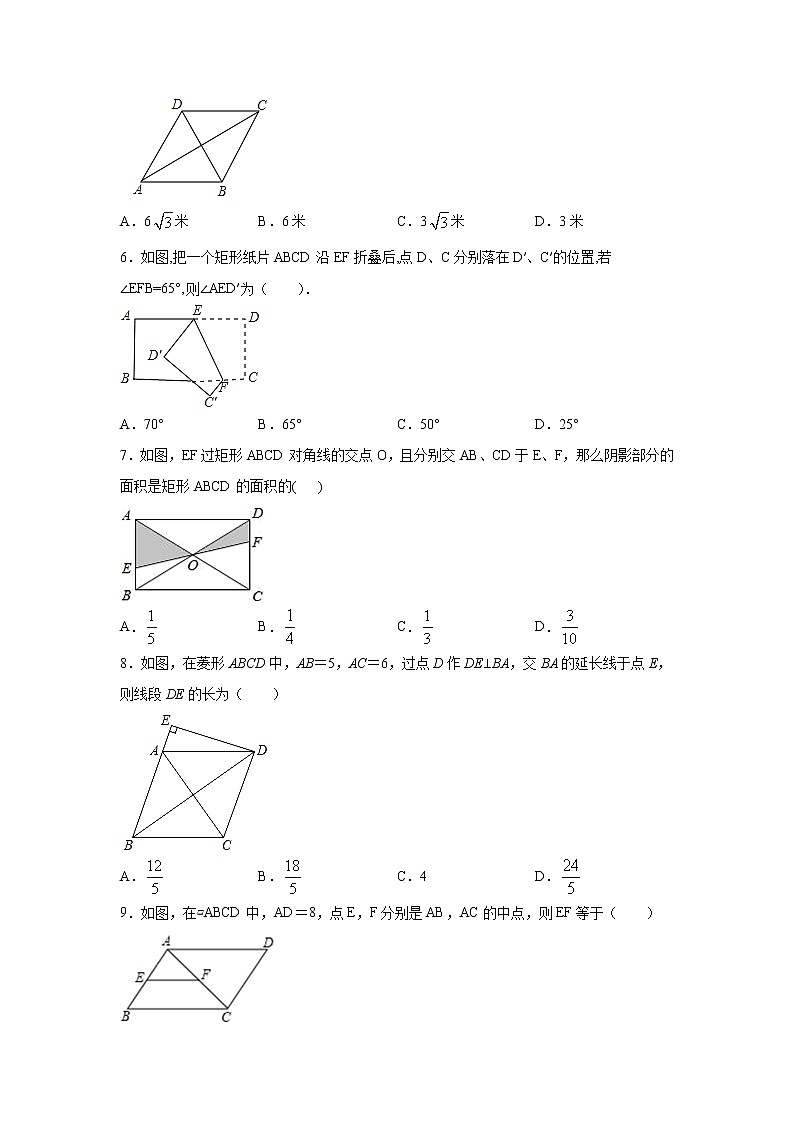
5．如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（　　）

A．6米 B．6米 C．3米 D．3米
6．如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′为（ ）．

A．70° B．65° C．50° D．25°
7．如图，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD的面积的( )

A． B． C． D．
8．如图，在菱形ABCD中，AB＝5，AC＝6，过点D作DE⊥BA，交BA的延长线于点E，则线段DE的长为（　　）

A． B． C．4 D．
9．如图，在▱ABCD中，AD＝8，点E，F分别是AB，AC的中点，则EF等于（　　）

A．2 B．3 C．4 D．5
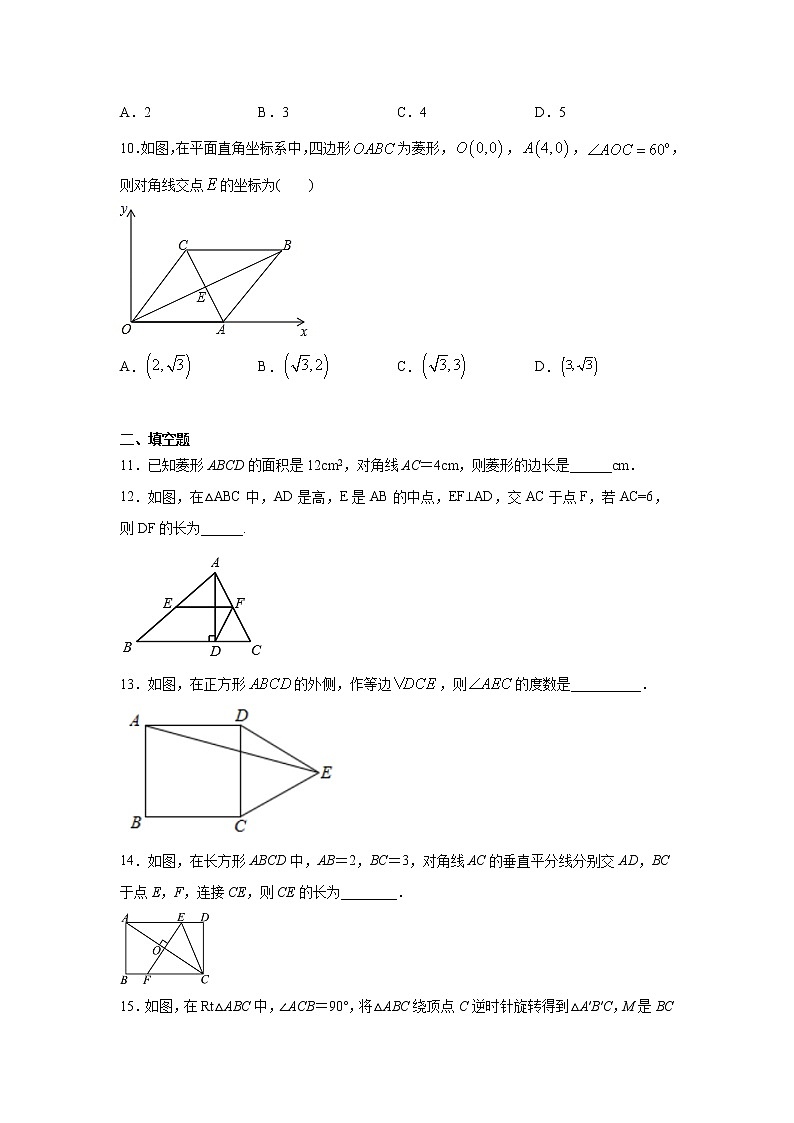
10．如图，在平面直角坐标系中，四边形为菱形，，，，则对角线交点的坐标为( )

A． B． C． D．


二、填空题
11．已知菱形ABCD的面积是12cm2，对角线AC＝4cm，则菱形的边长是______cm．
12．如图，在△ABC中，AD是高，E是AB的中点，EF⊥AD，交AC于点F，若AC=6，则DF的长为______.

13．如图，在正方形的外侧，作等边，则的度数是__________．

14．如图，在长方形ABCD中，AB＝2，BC＝3，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，则CE的长为________．

15．如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，P是A′B′的中点，连接PM，若BC＝2，∠BAC＝30°，则线段PM的最大值是_____．

16．如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形的边长为_____．

17．如图，O点是矩形ABCD的对角线的中点，菱形ABEO的边长为2，则BC＝ ______．

18．如图，在Rt△BAC和Rt△BDC中，∠BAC＝∠BDC＝90°，O是BC的中点，连接AO、DO．若AO＝3，则DO的长为_____．

19．如图，在矩形ABCD中，AB=3，AD=4，点P在AD上，PE⊥AC于E，PF⊥BD于F，则PE+PF等于_____．

20．如图，在正方形，E是对角线上一点，的延长线交于点F，连接．若，则______．

21．在直线l上依次摆放着七个正方形(如图所示)．已知斜放置的三个正方形的面积分别是a，b，c，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1＋S2＋S3＋S4＝_____．

22．如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝_____.

23．如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10，8），则点E的坐标为 .


三、解答题
24．如图，在四边形中，，延长到E，使，连接交于点F，点F是的中点．求证：
（1）．
（2）四边形是平行四边形．




25．如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD，
求证：四边形OCED是菱形．








26．在Rt△ABC中，∠BAC=90°,D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F
（1）求证：△AEF≌△DEB；
（2）证明四边形ADCF是菱形；
（3）若AC=4，AB=5，求菱形ADCF 的面积．

27．如图，在中，过点C作，E是AC的中点，连接DE并延长，交AB于点F，交CB的延长线于点G，连接AD，CF
求证：四边形AFCD是平行四边形．
若，，，求AB的长．











28．探究：如图1和2,四边形中,已知，，点，分别在、上，．
（1）①如图 1,若、都是直角，把绕点逆时针旋转至，使与重合，则能证得，请写出推理过程；
②如图 2，若、都不是直角，则当与满足数量关系_______时，仍有;
（2） 拓展：如图3,在中，,，点、均边
上,且．若，求的长．



参考答案
1．A
【分析】
根据轴对称图形的定义“平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形叫做轴对称图形”、中心对称图形的定义“平面内，把一个图形绕着某个点旋转，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形”逐项判断即可．
【详解】
A、是轴对称图形，也是中心对称图形，则此项符合题意
B、是轴对称图形，不是中心对称图形，则此项不符题意
C、不是轴对称图形，是中心对称图形，则此项不符题意
D、不是轴对称图形，也不是中心对称图形，则此项不符题意
故选：A．
【点拨】
本题考查了轴对称图形和中心对称图形的定义，熟记定义是解题关键．
2．B
【解析】
解：如图，

∵AE平分∠BAD交BC边于点E，
∴∠BAE=∠EAD，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC=5，
∴∠DAE=∠AEB，
∴∠BAE=∠AEB，
∴AB=BE=3，
∴EC=BC-BE=5-3=2．
故选B．
3．D
【解析】
试题分析：根据旋转角的定义，两对应边的夹角就是旋转角，即可求解．旋转角是∠CAC′=180°﹣30°=150°．
故选D．
考点：旋转的性质．
4．B
【分析】
直接利用中心对称图形的定义得出答案．
【详解】
解：如图所示：是中心对称图形．故选B．

【点拨】
此题主要考查了中心对称图形的定义，正确把握定义是解题关键．
5．A
【解析】
分析：本题考查的是菱形的性质，直角三角形的性质解决即可.
解析：因为菱形周长为24米，所以边长为6米，因为，所以∠BAO=30°，∴OA=米,∴AC= 米.

故选A.
6．C
【分析】
首先根据AD∥BC，求出∠FED的度数，然后根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等，则可知∠DEF=∠FED′，最后求得∠AED′的大小．
【详解】
解：∵AD∥BC，
∴∠EFB=∠FED=65°，
由折叠的性质知，∠DEF=∠FED′=65°，
∴∠AED′=180°-2∠FED=50°，
故选C．
【点拨】
此题考查了长方形的性质与折叠的性质．此题比较简单，解题的关键是注意数形结合思想的应用．
7．B
【分析】
根据矩形的性质，得△EBO≌△FDO，再由△AOB与△ABC同底且△AOB的高是△ABC高的得出结论．
【详解】
解：∵四边形为矩形，
∴OB＝OD＝OA＝OC，
在△EBO与△FDO中，
∵∠EOB＝∠DOF，
OB＝OD，
∠EBO＝∠FDO，
∴△EBO≌△FDO（ASA），
∴阴影部分的面积＝S△AEO＋S△EBO＝S△AOB，
∵△AOB与△ABC同底且△AOB的高是△ABC高的，
∴S△AOB＝S△ABC＝S矩形ABCD．
故选B．
【点拨】
本题考查矩形的性质，矩形具有平行四边形的性质，又具有自己的特性，要注意运用矩形具备而一般平行四边形不具备的性质
8．D
【分析】
利用菱形的面积等于两对角线之积的一半，求解菱形的面积，再利用等面积法求菱形的高即可．
【详解】
解：记AC与BD的交点为，
菱形,



菱形的面积

菱形的面积


故选D．

【点拨】
本题考查的是菱形的性质，菱形的面积公式，勾股定理．理解菱形的对角线互相垂直平分和学会用等面积法是解题关键．
9．C
【分析】
利用平行四边形性质得到BC长度，然后再利用中位线定理得到EF
【详解】
在▱ABCD中，AD＝8，得到BC=8，因为点E，F分别是AB，AC的中点，所以EF为△ABC的中位线，EF=，故选C
【点拨】
本题主要考查平行四边形性质与三角形中位线定理，属于简单题
10．D
【分析】
过点作轴于点，由直角三角形的性质求出长和长即可．
【详解】
解：过点作轴于点，
∵四边形为菱形，，
∴，OB⊥AC，，
∵，∴，
∴，
∴，，
∴，
∴．
故选D．

【点拨】
本题考查了菱形的性质、勾股定理及含30°直角三角形的性质，正确作出辅助线是解题的关键．
11．
【解析】
分析：根据菱形的面积公式求出另一对角线的长．然后因为菱形的对角线互相垂直平分，利用勾股定理求出菱形的边长．
详解：由菱形的面积公式，可得另一对角线长12×2÷4=6，
∵菱形的对角线互相垂直平分，
根据勾股定理可得菱形的边长=cm．
故答案为．
点拨：此题主要考查菱形的性质和菱形的面积公式，关键是掌握菱形的两条对角线互相垂直．
12．3
【分析】
根据中位线的性质得到F是AC中点，再根据直角三角形斜边上的中线是斜边的一半即可求解.
【详解】
∵AD是高，E是AB的中点，EF⊥AD，
∴EF是△ABC的中位线，
∴F点是AC中点，
∵AD是高，
∴△ACD是直角三角形，
∴DF=AC=3，
故填：3.
【点拨】
此题主要考查中位线与中线的性质，解题的关键是熟知中位线的判定与性质及直角三角形斜边上的中线是斜边的一半.
13．
【分析】
先求出的度数，即可求出.
【详解】
解：由题意可得，，



故答案为
【点拨】
本题考查了等腰与等边三角形的性质，等腰三角形的两底角相等，等边三角行的三条边都相等，三个角都相等，灵活应用等腰及等边三角形的性质是解题的关键.
14．
【解析】
EF垂直且平分AC，故AE=EC，AO=OC．
所以△AOE≌△COE．
设CE为x．
则DE=AD-x，CD=AB=2．
根据勾股定理可得x2=（3-x）2+22
解得CE=13/6．
15．3．
【分析】
连接PC．先依据直角三角形斜边上中线的性质求出PC＝2，再依据三角形的三边关系可得到PM≤PC+CM，由此可得到PM的最大值为PC+CM．
【详解】
解：如图连接PC．

在Rt△ABC中，∵∠A＝30°，BC＝2，
∴AB＝4，
根据旋转不变性可知，A′B′＝AB＝4，
∴A′P＝PB′，
∴PC＝ A′B′＝2，
∵CM＝BM＝1，
又∵PM≤PC+CM，即PM≤3，
∴PM的最大值为3（此时P、C、M共线）．
故答案为3．
【点拨】
本题考查旋转的性质，直角三角形的性质、三角形的三边关系，解题的关键是掌握本题的辅助线的作法．
16．（）n﹣1
【详解】
解：∵四边形ABCD为正方形，
∴AB=BC=1，∠B=90°，∴AC=；
同理可求：AE=，HE=，…，
∴第n个正方形的边长an=．
故答案为．
17．2
【分析】
根据矩形的性质得到AC=4，再根据菱形的性质得到AB=2，再根据勾股定理即可求解.
【详解】
∵菱形的边长为2，∴AB=AO=2，
∵O点是矩形ABCD的对角线的中点，
∴AC=2AO=4，
∴BC=
故填：2
【点拨】
此题主要考查菱形的性质，解题的关键是熟知菱形的四边相等.
18．3
【分析】
根据直角三角形斜边的中线等于斜边的一半求解即可.
【详解】
∵在Rt△BAC和Rt△BDC中，∠BAC＝∠BDC＝90°，O是BC的中点，
∴,,
∴DO=AO=3.
故答案为3.
【点拨】
本题考查了直角三角形的性质，熟练掌握直角三角形斜边的中线等于斜边的一半是解答本题的关键.
19．
【详解】
解：设AC与BD相交于点O，连接OP，过D作DM⊥AC于M，

∵四边形ABCD是矩形，
∴，AC=BD，∠ADC=90°．
∴OA=OD．
∵AB=3，AD=4，∴由勾股定理得：AC= ．
∵ ，∴DM=．
∵，
∴ ．
∴PE+PF=DM=．故选B．
20．
【分析】
先证明，得到，可得到，再根据平行线的性质得到，可得，根据三角形内角和定理即可求解；
【详解】
∵四边形ABCD是正方形，
∴AB=CB，AB∥CD，
又∵BD是角平分线，
∴，
又∵，
∴，
∴，
在和中，
，
∴，
∴，
∴，
∴．
故答案是．
【点拨】
本题主要考查了利用正方形的性质求角度，准确利用三角形全等和三角形内角和定理求解是解题的关键．
21．a+c
【分析】
运用勾股定理可知，每两个相邻的正方形面积和都等于中间斜放的正方形面积，据此即可解答,具体: 求证△ABC≌△CDE，得DE=BC，△ABC中AB2+CE2=AC2，根据S3=AB2，S4=DE2可求得S3+S4=c，同理可得S1+S2=a，故S3+S4+S1+S2=a+c．．
【详解】
解：

∵∠ACB+∠DCE=90°，∠BAC+∠ACB=90°，
∴∠DCE=∠BAC，
∵AC=CE，∠ABC=∠CDE
∴△ABC≌△CDE，
∴BC=DE，
在直角△ABC中，AB2+BC2=AC2，
即，AB2+DE2=AC2，
∵S3=AB2，S4=DE2
∴S3+S4=c
同理S1+S2=a
故可得S1+S2+S3+S4=a+c，
故答案是： a+c．
【点拨】
本题考查正方形面积的计算，正方形各边相等的性质，全等三角形的判定．解题关键是本题中根据△ABC≌△CDE证明S3+S4=c
22．6
【解析】
分析：根据BD=CD，AB=CD，可得BD=BA，再根据AM⊥BD，DN⊥AB，即可得到DN=AM=3，依据∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，即可得到△APM是等腰直角三角形，进而得到AP=AM=6．
详解：∵BD=CD，AB=CD，
∴BD=BA，
又∵AM⊥BD，DN⊥AB，
∴DN=AM=3，
又∵∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，
∴∠P=∠PAM，
∴△APM是等腰直角三角形，
∴AP=AM=6，
故答案为6．
点拨：本题主要考查了平行四边形的性质以及等腰直角三角形的性质的运用，解决问题给的关键是判定△APM是等腰直角三角形．
23．（10，3）
【分析】
根据折叠的性质得到AF=AD，所以在直角△AOF中，利用勾股定理求得OF=6，然后设EC=x，则EF=DE=8-x，CF=10-6=4，根据勾股定理列方程求出EC可得点E的坐标．
【详解】
∵四边形AOCD为矩形,D的坐标为(10,8),
∴AD=BC=10，DC=AB=8，
∵矩形沿AE折叠，使D落在BC上的点F处，
∴AD=AF=10，DE=EF，
在Rt△AOF中,OF= =6，
∴FC=10−6=4，
设EC=x，则DE=EF=8−x，
在Rt△CEF中,EF2=EC2+FC2，
即(8−x)2=x2+42，
解得x=3，即EC的长为3.
∴点E的坐标为(10,3).
24．（1）见解析；（2）见解析
【分析】
（1）根据全等三角形的判定定理（AAS）进行判断；
（2）根据全等三角形的性质和平行四边形判定定理，即可得到答案.
【详解】
证明：（1）∵，
∴，
∵点F是的中点，
∴，
在与中，，
∴；
（2）∵，
∴，
∵，
∴，
∵，
∴四边形是平行四边形．
【点拨】
本题考查全等三角形的判定和性质、平行四边形判定定理，解题的关键是熟练掌握全等三角形的判定和性质、平行四边形判定定理.
25．见解析
【分析】
首先根据两对边互相平行的四边形是平行四边形证明四边形OCED是平行四边形，再根据矩形的性质可得OC=OD，即可利用一组邻边相等的平行四边形是菱形判定出结论．
【详解】
证明：∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形．
∵四边形ABCD是矩形，∴OC=OD=AC=BD
∴四边形OCED是菱形．
26．（1）证明详见解析；（2）证明详见解析；（3）10．
【分析】
（1）利用平行线的性质及中点的定义，可利用AAS证得结论；
（2）由（1）可得AF=BD，结合条件可求得AF=DC，则可证明四边形ADCF为平行四边形，再利用直角三角形的性质可证得AD=CD，可证得四边形ADCF为菱形；
（3）连接DF，可证得四边形ABDF为平行四边形，则可求得DF的长，利用菱形的面积公式可求得答案．
【详解】
（1）证明：∵AF∥BC，
∴∠AFE=∠DBE，
∵E是AD的中点，
∴AE=DE，
在△AFE和△DBE中，

∴△AFE≌△DBE（AAS）；
（2）证明：由（1）知，△AFE≌△DBE，则AF=DB．
∵AD为BC边上的中线
∴DB=DC，
∴AF=CD．
∵AF∥BC，
∴四边形ADCF是平行四边形，
∵∠BAC=90°，D是BC的中点，E是AD的中点，
∴AD=DC=BC，
∴四边形ADCF是菱形；
（3）连接DF，

∵AF∥BD，AF=BD，
∴四边形ABDF是平行四边形，
∴DF=AB=5，
∵四边形ADCF是菱形，
∴S菱形ADCF=AC▪DF=×4×5=10．
【点拨】
本题主要考查菱形的性质及判定，利用全等三角形的性质证得AF=CD是解题的关键，注意菱形面积公式的应用．
27．证明见解析；．
【分析】
由E是AC的中点知，由知，据此根据“AAS”即可证≌，从而得，结合即可得证；
证∽得，据此求得，由及可得答案．
【详解】
是AC的中点，
，
，
，
在和中，
，
≌，
，
又，即，
四边形AFCD是平行四边形；
，
∽，
，即，
解得：，
四边形AFCD是平行四边形，
，
．
【点拨】
本题考查了平行四边形的判定与性质，全等三角形的判定与性质，相似三角形的判定与性质，熟练掌握相关的性质及定理是解题的关键.
28．（1）①见解析；②，理由见解析；（2）
【分析】
（1）①根据旋转的性质得出AE＝AG，∠BAE＝∠DAG，BE＝DG，求出∠EAF＝∠GAF＝45°，根据SAS推出△EAF≌△GAF，根据全等三角形的性质得出EF＝GF，即可求出答案；
②根据旋转的性质得出AE＝AG，∠B＝∠ADG，∠BAE＝∠DAG，求出C、D、G在一条直线上，根据SAS推出△EAF≌△GAF，根据全等三角形的性质得出EF＝GF，即可求出答案；
（2）根据等腰直角三角形性质好勾股定理求出∠ABC＝∠C＝45°，BC＝4，根据旋转的性质得出AF＝AE，∠FBA＝∠C＝45°，∠BAF＝∠CAE，求出∠FAD＝∠DAE＝45°，证△FAD≌△EAD，根据全等得出DF＝DE，设DE＝x，则DF＝x，BF＝CE＝3−x，根据勾股定理得出方程，求出x即可．
【详解】
（1）①如图1，
∵把绕点逆时针旋转至，使与重合，
∴，，
∵，，
∴，
∴，
即，
在和中

∴，
∴，
∵，
∴；
②，

理由是：
把绕点旋转到，使和重合，
则，，，
∵，
∴，
∴，，在一条直线上，
和①知求法类似，，
在和中

∴，
∴，
∵，
∴；
故答案为：
（2）∵中，，
∴，由勾股定理得：
，
把绕点旋转到,使和重合，连接．
则，，，

∵，
∴，
∴，
在和中

∴，
∴，
设，则，
∵，
∴，
∵，，
∴，
由勾股定理得：，
，
解得：，
即．
【点拨】本题考查了旋转的性质，全等三角形的性质和判定，勾股定理的应用，此题是开放性试题，首先在特殊图形中找到规律，然后再推广到一般图形中，对学生的分析问题，解决问题的能力要求比较高．