2020-2021学年27.2.2 相似三角形的性质导学案及答案

这是一份2020-2021学年27.2.2 相似三角形的性质导学案及答案，共6页。学案主要包含了学习目标，要点梳理，典型例题，思路点拨，答案与解析，总结升华等内容，欢迎下载使用。
相似三角形的判定--知识讲解（提高）【学习目标】1、了解相似三角形的概念， 掌握相似三角形的表示方法及判定方法；2、进一步探索相似三角形的判定及其应用，提高运用“类比”思想的自觉性，提高推理能力.【要点梳理】要点一、相似三角形在和中，如果我们就说与相似，记作∽.k就是它们的相似比，“∽”读作“相似于”.要点诠释：
(1)书写两个三角形相似时，要注意对应点的位置要一致，即∽，则说明点A的对应点是A′，点B的对应点是B′，点C的对应点是C′；(2)对于相似比，要注意顺序和对应的问题，如果两个三角形相似，那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时，两个三角形全等.要点二、相似三角形的判定定理1．判定方法（一）：平行于三角形一边的直线和其他两边相交，所构成的三角形和原三角形相似；2．判定方法（二）：如果两个三角形的三组对应边的比相等，那么这两个三角形相似；　3．判定方法（三）：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似.要点诠释：此方法要求用三角形的两边及其夹角来判定两个三角形相似，应用时必须注意这个角必需是两边的夹角，否则，判断的结果可能是错误的. 4．判定方法（四）：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似.
要点诠释：要判定两个三角形是否相似，只需找到这两个三角形的两个对应角相等即可，对于直角三角形而言，若有一个锐角对应相等，那么这两个三角形相似.
要点三、相似三角形的常见图形及其变换：【典型例题】类型一、相似三角形1. 判断对错：
　　(1)两个直角三角形一定相似吗？为什么？
　　(2)两个等腰三角形一定相似吗？为什么？
　　(3) 两个等边三角形一定相似吗？为什么？【思路点拨】注意相似三角形判定定理的灵活运用.【答案与解析】(1).不一定相似，反例：
直角三角形只确定一个直角，其他的两对角可能相等，也可能不相等.
所以直角三角形不一定相似.
(2)不一定相似，反例：
等腰三角形中只有两边相等，而底边不固定.因此两个等腰三角形中有两边对应成比例，两底边的比不一定等于对应腰的比，所以等腰三角形不一定相似.(3) 一定相似.
因为等边三角形各边都相等，各角都等于60度，所以两个等边三角形对应角相等，对应边成比例，因此两个等边三角形一定相似.【总结升华】要说明两个三角形相似，要同时满足对应角相等，对应边成比例.要说明不相似，则只要否定其中的一个条件.举一反三：【变式】下列说法错误的是（   ）． 
　　A．有一对锐角对应相等的两个直角三角形相似　　B．全等的两个三角形一定相似
　　C．对应角相等的两个多边形相似 　　   D．两条邻边对应成比例的两个矩形相似【答案】C.类型二、相似三角形的判定2.（2015•湖州模拟）如图，在正方形ABCD中，E、F分别是边AD、CD上的点，，连接EF并延长交BC的延长线于点G．（1）求证：△ABE∽△DEF；（2）若正方形的边长为4，求BG的长．【思路点拨】（1）利用正方形的性质，可得∠A=∠D，根据已知可得，根据有两边对应成比例且夹角相等三角形相似，可得△ABE∽△DEF；（2）根据平行线分线段成比例定理，可得CG的长，即可求得BG的长．【答案与解析】（1）证明：∵ABCD为正方形，∴AD=AB=DC=BC，∠A=∠D=90°，∵AE=ED，∴，∵DF=DC，∴，∴，∴△ABE∽△DEF；（2）解：∵ABCD为正方形，∴ED∥BG，∴，又∵DF=DC，正方形的边长为4，∴ED=2，CG=6，∴BG=BC+CG=10．【总结升华】此题考查了相似三角形的判定、正方形的性质、平行线分线段成比例定理等知识的综合应用．解题的关键是数形结合思想的应用．举一反三：
【变式】（2015•大庆模拟）如图，△ABC中，AB=5，BC=3，CA=4，D为AB的中点，过点D的直线与BC交于点E，若直线DE截△ABC所得的三角形与△ABC相似，则DE=　　．【答案】解：∵D为AB的中点，∴BD=AB=，∵∠DBE=∠ABC，∴当∠DBE=∠ACB时，△BDE∽△BAC时，如图1，则=，即=，解得DE=2；当∠BDE=∠ACB时，如图2，DE交AC于F，∵∠DAF=∠CAB，∴△ADF∽△ACB，∴△BDE∽△BCA，∴=，即=，解得DE=，综上所述，若直线DE截△ABC所得的三角形与△ABC相似，则DE=2或．【高清课程名称：  相似三角形的判定（1）   高清ID号： 394497关联的位置名称（播放点名称）：练习4】 3.如图，小正方形边长均为1，则图中的三角形（阴影部分）与相似的是哪一个？
　　　　        　　   
　　　 图（1）　　　  图（2）　　　    　 图（3）　　　　　     图（4）
【答案与解析】图中的三角形为格点三角形，可根据勾股定理求出各边的长，然后根据三    角形三边的长度的比是否相等来判断哪两个三角形相似．
　　   由勾股定理知，，．
　　　　图（1）中，三角形的三边长分别为1，，．
　　　　图（2）中，三角形的三边长分别为1，，．
　　　　图（3）中，三角形的三边长分别为，，3．
　　　　图（4）中，三角形的三边长分别为2，，．
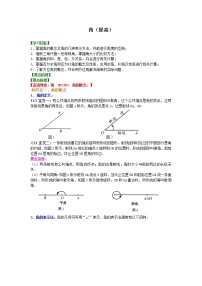
　　　　由于，故图（2）中的三角形和相似．【总结升华】判断三边是否成比例，应先将三边按大小顺序排列，然后分别计算它们对应边的比，最后由比值是否相等来确定两个三角形是否相似．4. 已知：如图，，，，当BD与a、b之间满足怎样的关系时，这两个三角形相似？     
 【答案与解析】由于两个三角形是直角三角形，所以只要有夹直角两边的比相等，就有两个  三角形相似．
         ，∴（1）当时，∽．
　　　　 　　此时，，即，．
　　　　　　 即当时，∽．
　　　　（2）当时，∽．
　　　　　　 此时，，即，．
　　　　　　 即当时，∽．
　　　　  综上所述，当或时，这两个三角形相似．
【总结升华】本题仍是考虑两个三角形有一个角相等时，夹这两个角两边的比相等时有两种情况．举一反三：
【变式】如图，正方形ABCD和等腰Rt，其中，G是CD与EF的交点．
　　（1）求证：≌．
　　（2）若，，，求的值．
　　　　　　　　　　　　　　　 
　　【答案】（1）证明：∵四边形ABCD是正方形，
　　　　　　 　，．
　　　　　　 　是等腰直角三角形，，
　　　　　　 　，，≌．
　　        （2）解：在中，，，，
　　　　　　   ．
　　　　　　   ≌，
　　　　　　  ∴DE=BF=4，∠DEC=∠BFC=90°.
　　　　　　  ∵∠EDC+∠DCE=90°，∠FCD+∠DCE=90°.
　　　　　　  ∴∠EDC=∠FCD.
　　　　　　  ∴ ∴∽,
　　　　　　  ．