2021年北京海淀区北航实验学校八年级下期末数学试卷

这是一份2021年北京海淀区北航实验学校八年级下期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 用公式法解方程 x2−2=−3x 时，a，b，c 的值依次是
A. 0，−2，−3B. 1，3，−2C. 1，−3，−2D. 1，−2，−3

2. 三角形的外角和等于
A. 90∘B. 180∘C. 360∘D. 540∘

3. 下列两个电子数字成中心对称的是
A. B.
C. D.

4. 在函数 y=x−3x−4 中，自变量 x 的取值范围是
A. x>3B. x≥3
C. x>4D. x≥3 且 x≠4

5. 在平面直角坐标系中，把点 P−3,2 绕原点 O 顺时针旋转 180∘，所得到的对应点 Pʹ 的坐标为
A. 3,2B. 2,−3C. −3,−2D. 3,−2

6. 下列各统计量中，表示一组数据波动程度的量是
A. 平均数B. 众数C. 方差D. 频数

7. 方程 x2+x−12=0 的两个根为
A. x1=−2，x2=6B. x1=−6，x2=2C. x1=−3，x2=4D. x1=−4，x2=3

8. 某种植基地 2016 年蔬菜产量为 80 吨，预计 2018 年蔬菜产量达到 100 吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为 x，则可列方程为
A. 801+x2=100B. 1001−x2=80
C. 801+2x=100D. 801+x2=100

9. 如图，在平行四边形 ABCD 中，BF 平分 ∠ABC，交 AD 于点 F，CE 平分 ∠BCD，交 AD 于点 E，AB=6，EF=2，则 BC 的长为
A. 8B. 10C. 12D. 14

10. 如图 1 所示，在矩形 MNPQ 中，动点 R 从点 N 出发，沿 N→P→Q→M 方向运动至点 M 处停止，设点 R 运动的路程为 x，△MNR 的面积为 y，如果 y 关于 x 的函数图象如图 2 所示，则矩形 MNPQ 的周长是
A. 9B. 18C. 13D. 6

二、填空题（共8小题；共41分）
11. 如图，已知，OB=2，△ABC 三个顶点坐标分别是：
A（ ， ）；
B（ ， ）；
C（ ， ）．

12. 一组数据：−1，3，2，0，4 的极差是 ．

13. 若一次函数的图象与直线 y=−3x 平行，且经过点 1,2，则一次函数的表达式为 ．

14. 如图 △ABC 的周长是 10 cm，则联结它的三边的中点所得的三角形 DEF 的周长为 cm．

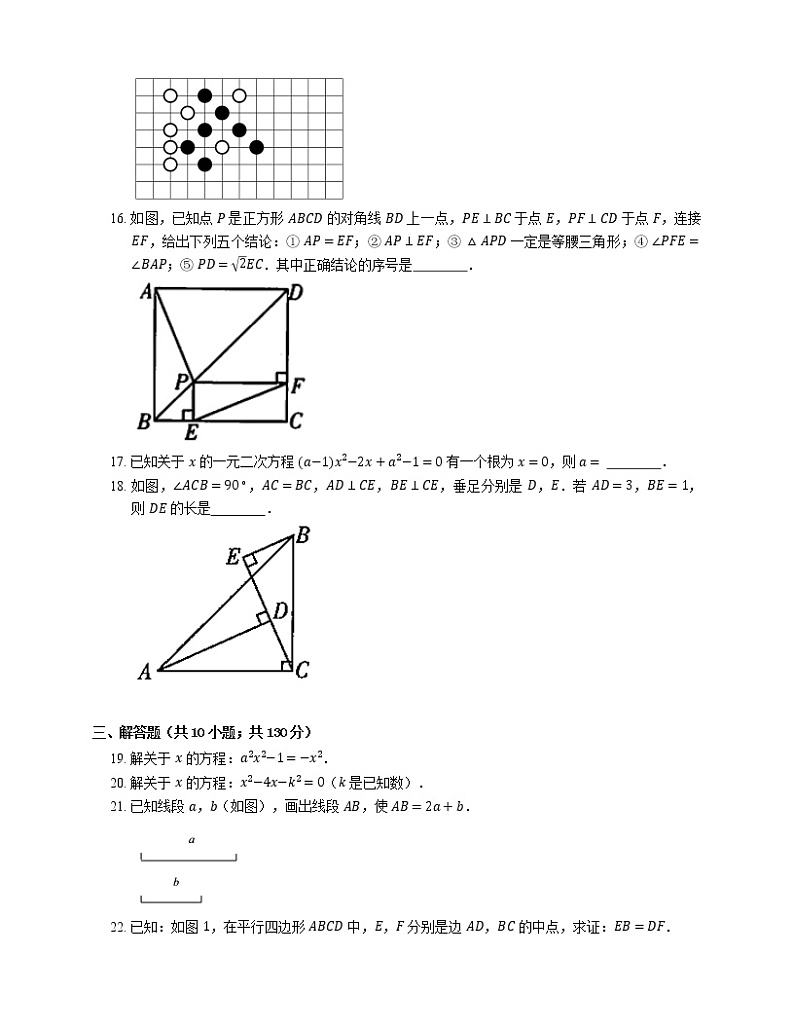
15. 同学们玩过五子棋吗?它的比赛规则是只要同色 5 子先成一条直线就算胜，如图是两人玩的一盘棋，若白的位置是 1,−5，黑的位置是 2,−4，现轮到黑棋走，你认为黑棋放在 位置就获得胜利了．

16. 如图，已知点 P 是正方形 ABCD 的对角线 BD 上一点，PE⊥BC 于点 E，PF⊥CD 于点 F，连接 EF，给出下列五个结论：① AP=EF；② AP⊥EF；③ △APD 一定是等腰三角形；④ ∠PFE=∠BAP；⑤ PD=2EC．其中正确结论的序号是 ．

17. 已知关于 x 的一元二次方程 a−1x2−2x+a2−1=0 有一个根为 x=0，则 a= ．

18. 如图，∠ACB=90∘，AC=BC，AD⊥CE，BE⊥CE，垂足分别是 D，E．若 AD=3，BE=1，则 DE 的长是 ．

三、解答题（共10小题；共130分）
19. 解关于 x 的方程：a2x2−1=−x2．

20. 解关于 x 的方程：x2−4x−k2=0（k 是已知数）．

21. 已知线段 a，b（如图），画出线段 AB，使 AB=2a+b．

22. 已知：如图 1，在平行四边形 ABCD 中，E，F 分别是边 AD，BC 的中点，求证：EB=DF．

23. 如图所示，一次函数 y=kx+b 的图象经过 A2,4 和 B0,2 两点，且与 x 轴相交于 C 点，连接 AO．
（1）求该一次函数的关系式；
（2）求 △AOC 的面积．

24. 已知关于 x 的一元二次方程 x2+2x+2k−4=0 有两个不相等的实数根．
（1）求 k 的取值范围；
（2）若 k 为正整数，且该方程的根都是整数，求 k 的值及该方程的根．

25. 为了解居民月用水量，某市对居民用水进行了抽样调查，并制成直方图．
（1）这次一共抽查了 户；
（2）用水量不足 10 吨的有 户，用水量超过 16 吨的有 户；
（3）假设该区有 8 万户居民，估计用水量少于 10 吨的有多少户?

26. 在网格中（每一个小正方形的边长为 1），顶点是格点的四边形我们称为格点四边形．
（1）请你在网格①中画一个以 AB 为边的格点平行四边形，使其对角线长为 17；
（2）请你在网格②中画一个以 AB 为边的格点菱形．

27. 有这样一个问题：探究函数 y=∣x+1∣ 的图象与性质．
小明根据学习一次函数的经验，对函数 y=∣x+l∣ 的图象与性质进行了探究．
下面是小明的探究过程，请补充完整：
（1）函数 y=∣x+1∣ 的自变量 x 的取值范围是 ；
（2）如表是 x 与 y 的几组对应值．
x⋯−5−4−3−2−10123⋯y⋯432m01234⋯m
的值为 ；
（3）在如图网格中，建立平面直角坐标系 xOy，描出表中各对对应值为坐标的点，并画出该函数的图象；
（4）小明根据画出的函数图象，得出了如下几条结论：
①函数有最小值为 0；
②当 x>−1 时，y 随 x 的增大而增大；
③图象关于过点 −1,0 且垂直于 x 轴的直线对称．
小明得出的结论中正确的是 ．（只填序号）

28. 在平面直角坐标系中，已知点 A2−m,0，B2+m,0，分别度过点 A 、点 B 作 x 轴的垂线 a，b，由垂线 a，b 组成的图形称为“H 型”，已知点 C−1,−1，D3,3，连接 CD．
（1）当 m=2 时，线段 CD（包括 C，D）与“H 型”的公共点坐标为 ．
（2）若线段 CD（包括 C，D）与“H 型”恰有两个公共点，则 m 的取值范围为 ．
（3）在线段 CD（包括 C，D）上任取一点 Px1,y1，过点 P 作 x 轴的平行线，与“H 型”分别交于两点 Mx2,y2，点 Nx3,y3，令 t=x1+x2+x3，求 t 的取值范围．
答案
第一部分
1. B【解析】整理得 x2+3x−2=0，这里 a=1，b=3，c=−2．
2. C【解析】三角形外角和为 360∘．
故选：C．
3. A
4. D
5. D
【解析】根据题意得，点 P 关于原点的对称点是点 Pʹ，∵P 点的坐标为 −3,2，∴ 点 Pʹ 的坐标为 3,−2．
6. C【解析】能反映一组数据波动程度的是方差或标准差．
7. D
8. A
9. B【解析】∵ 四边形 ABCD 是平行四边形，
∴AD∥BC，CD=AB=6，BC=AD，
∴∠2=∠3，∠6=∠5，
∵BF 平分 ∠ABC，CE 平分 ∠BCD，
∴∠1=∠2，∠4=∠5，
∴∠1=∠3，∠4=∠6，
∴AF=AB=6，DE=DC=6，
∴AE=AF−EF=6−2=4，
∴AD=AE+DE=4+6=10，
∴BC=AD=10．
10. B
【解析】∵x=4 时，点 R 从 N 到达点 P，
此时面积开始不变，
∴PN=4，
∵ 当 x=9 时，点 R 从 P 到达 Q 点，
此时面积开始减小，
∴QP=9−4=5，
∴矩形MNPQ的周长=2PN+QP=2×4+5=2×9=18.
第二部分
11. −2，3，2，0，−1，−1
12. 5
【解析】∵ 数据：−1，3，2，0，4 的最大数为 4 、最小数为 −1，
∴ 极差为 4−−1=5．
13. y=−3x+5
14. 5
【解析】根据 D，E 分别是 AB 和 AC 的中点，得到 DE∥BC，并且 BC=2DE．
同理，根据 E，F 分别是 AC 和 BC 的中点，得到 EF∥AB，并且 AB=2EF．
根据 D，F 分别是 AB 和 BC 的中点，得到 DF∥AC，并且 AC=2DF．
所以，三角形 DEF 的周长 =DE+EF+FD=12BC+AB+AC=5 cm．
15. 2,0 或 7,−5
【解析】∵ 白的位置是 1,−5，黑的位置是 2,−4，
∴ 如图黑棋放在两圆所在位置，就获得胜利了，
∴ 与 1,−5 在一条水平线上点的坐标为：7,−5，
另一点的坐标为：2,0，
两点的坐标为：2,0 或 7,−5．
16. ①②④⑤
17. −1
18. 2
第三部分
19. 移项得
a2x2+x2=1.
合并同类项得
a2+1x2=1,∵a2+1≠0
．
∴ 化简得
x2=1a2+1.∵a2≥0
；
∴a2+1>0．
∴ 解得
x=±a2+1a2+1.∴
原方程的根是 x1=a2+1a2+1，x1=−a2+1a2+1．
20. 2+k2+4，2−k2+4．
21. 如图所示：
22. ∵ 四边形 ABCD 是平行四边形，
∴AD∥BC，AD=BC．
∵ED=12AD，BF=12BC．
∴ED∥BF，ED=BF．
∴ 四边形 BFDE 是平行四边形．
∴EB=DF．
23. （1） 根据题意，得 2k+b=4，b=2，
则 2k+2=4，解得 k=1，
所以该一次函数的关系式为 y=x+2．
（2） 由（1）知，该一次函数的关系式为 y=x+2．
令 y=0，得 0=x+2，解得 x=−2，
所以 C 点的坐标为 −2,0，
所以 OC=∣−2∣=2．
所以 S△AOC=12OC⋅yA=12×2×4=4．
24. （1） 依题意，得 Δ=22−42k−4>0，
解得 k<52．
（2） 由（1）得 k<52，
∵k 为正整数，
∴k=1或2，
当 k=1 时，方程化为 x2+2x−2=0，
解得 x1=3−1，x2=−3−1，不符合题意，
当 k=2 时，方程化为 x2+2x=0，
解得 x1=0，x2=−2，符合题意．
综上，k 的值为 2，方程的根为 x1=0，x2=−2．
25. （1） 100
（2） 55；10
（3） 55100×80000=44000（户）．
答：估计该区居民用水量少于 10 吨的有 44000 户．
26. （1） 所作图形如下：
（2） 所作图形如下：
27. （1） x 为任意实数
【解析】在函数 y=∣x+1∣ 中，自变量 x 的取值范围是 x 为任意实数．
（2） 1
【解析】当 x=−2 时，m=∣−2+1∣=1．
（3） 画出函数的图象如图：
（4） ①②③
【解析】由函数图象可知，
①函数有最小值为 0，正确；
②当 x>−1 时，y 随 x 的增大而增大，正确；
③图象关于过点 −1,0 且垂直于 x 轴的直线对称，正确．
28. （1） 0,0，22,22
【解析】当 m=2 时，A0,0，B22,0，
∵C−1,−1，D3,3，
∴ 线段 CD 经过第一、三象限角平分线 y=x 上，即 CD 过原点，
∴ 点 A 在线段 CD 上，当 x=22 时，y=22，
∴ 线段 CD 与“H”型的公共点坐标为 0,0，22,22．
（2） 0【解析】∵ 线段 CD 与“H”型恰有 2 个公共点，
∴ 当 m>0 时，2+m<3，
∴0当 m<0 时，2−m<3，
∴2−3 ∴m 的取值范围是 0 （3） 依题意可知，A2−m,0，B2+m,0，
∴A，B 关于点 2,0 对称，
∵ 过点 P 作 x 轴的平行线与“H”型交于点 Mx2,y2，Nx3,y3，
∴M，N 关于 2,y2 对称，
∴x2+x3=22，
∵−1≤x1≤3，
∴−1+22≤x1+x1+x3≤3+22，
即 −1+22≤t≤3+22，
∴t 的取值范围是 −1+22≤t≤3+22．