2021年北京大兴区北京市国际艺术学校（初中部）八年级下期末数学试卷

这是一份2021年北京大兴区北京市国际艺术学校（初中部）八年级下期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 若方程 a−1x2+x−9=0 是关于 x 的一元二次方程，则 a 的取值范围是
A. a≠0B. a≠1C. a≠−1D. a>1

2. 在平面直角坐标系中，一个长方形三个顶点的坐标为 −1,−1，−1,2，3,−1，则第四个顶点的坐标为
A. 2,2B. 3,2C. 3,3D. 2,3

3. 方程 x2+x−12=0 的两个根为
A. x1=−2，x2=6B. x1=−6，x2=2C. x1=−3，x2=4D. x1=−4，x2=3

4. 在某中学举行的演讲比赛中，初一年级 5 名参赛选手的成绩如下表所示，请你根据表中提供的数据，计算出这 5 名选手成绩的方差为
选手1号2号3号4号5号平均成绩得分9095■898891
A. 2B. 6.8C. 34D. 93

5. 若一元二次方程 4x2+12x−1147=0 的两根为 a，b，且 a>b，则 3a+b 的值为
A. 22B. 28C. 34D. 40

6. 均匀地向如图中的容器注水，最后把容器注满，在注水过程中，水面高度 h 随时间 t 的变化的图象是
A. B.
C. D.

7. 下列图形中，既是中心对称图形也是轴对称图形的是
A. B.
C. D.

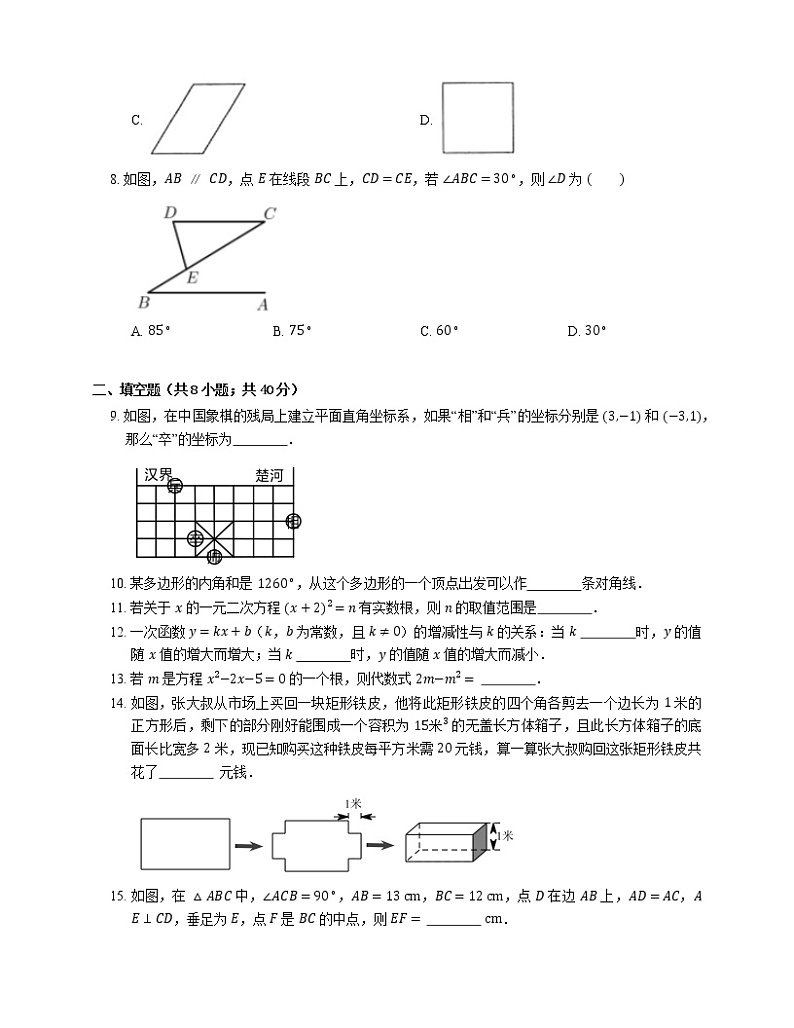
8. 如图，AB∥CD，点 E 在线段 BC 上，CD=CE，若 ∠ABC=30∘，则 ∠D 为
A. 85∘B. 75∘C. 60∘D. 30∘

二、填空题（共8小题；共40分）
9. 如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是 3,−1 和 −3,1，那么“卒”的坐标为 ．

10. 某多边形的内角和是 1260∘，从这个多边形的一个顶点出发可以作 条对角线．

11. 若关于 x 的一元二次方程 x+22=n 有实数根，则 n 的取值范围是 ．

12. 一次函数 y=kx+b（k，b 为常数，且 k≠0）的增减性与 k 的关系：当 k 时，y 的值随 x 值的增大而增大；当 k 时，y 的值随 x 值的增大而减小．

13. 若 m 是方程 x2−2x−5=0 的一个根，则代数式 2m−m2= ．

14. 如图，张大叔从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为 1 米的正方形后，剩下的部分刚好能围成一个容积为 15米3 的无盖长方体箱子，且此长方体箱子的底面长比宽多 2 米，现已知购买这种铁皮每平方米需 20 元钱，算一算张大叔购回这张矩形铁皮共花了 元钱．

15. 如图，在 △ABC 中，∠ACB=90∘，AB=13 cm，BC=12 cm，点 D 在边 AB 上，AD=AC，AE⊥CD，垂足为 E，点 F 是 BC 的中点，则 EF= cm．

16. 某公司员工的月工资如表：
员工经理副经理职员A职员B职员C职员D职员E职员F杂工G月工资/元1000074005400500049004800480048004200
经理、职员 C 、职员 D 从不同的角度描述了该公司员工的收入情况．
经理：我公司员工收入很高，月平均工资为 5700 元．
职员 C：我的工资是 4900 元，在公司算中等收入．
职员 D：我们好几个人工资都是 4800 元．
应聘者：这个公司员工收入到底怎样呢?
设该公司员工的月工资数据（见上述表格）的平均数、中位数、众数分别为 k，m，n，请根据上述信息完成下列问题：
（1）k= ，m= ，n= ；
（2）上月一个员工辞职了，从本月开始，停发该员工工资，若本月该公司剩下的 8 名员工的月工资不变，但这 8 名员工的月工资数据（单位：元）的平均数比原 9 名员工的月工资数据（见上述表格）的平均数减小了你认为辞职的那名员工可能是 ．

三、解答题（共12小题；共156分）
17. 解方程 x2+4=4x．

18. 如图，平行四边形 ABCD 的对角线 AC，BD 相交于点 O，EF 过点 O 与 BA，DC 的延长线分别相交于点 E，F．求证：OE=OF．

19. 关于 x 的一元二次方程 x2−2m+1x+m2=0 有两个实数根．
（1）求 m 的取值范围；
（2）写出一个满足条件的 m 的值，并求此时方程的根．

20. 如图，已知一次函数的图象与 x 轴交于点 A−6,0，交正比例函数图象于点 B，且点 B 在第二象限，它的横坐标为 −4，△AOB 的面积为 15，求这两个函数的解析式．

21. 如图，平行四边形 ABCD 的两条对角线相交于点 O，点 E 是 DO 的中点，点 F 是 BO 的中点，连接 AE，CE，AF，CF．
试说明 AE 与 CF 的关系，并说明理由．

22. 已知关于 x 的一元二次方程 mx2−4m+2x+3m+6=0．
（1）试讨论该方程的根的情况；
（2）无论 m 为何值，该方程都有一个固定的实数根，试求出这个根．

23. 如图所示，在四边形 ABCD 中，已知 AB:BC:CD:DA=2:2:3:1，且 ∠B=90∘，试求 ∠DAB 的度数．

24. 在平面直角坐标系 xOy 中，点 A−1,m 是直线 y=−x+2 上一点，点 A 向右平移 4 个单位长度得到点 B．
（1）求点 A，B 的坐标．
（2）若直线 l:y=kx−2k≠0 与线段 AB 有公共点，结合函数的图象，求 k 的取值范围．

25. 从甲、乙两名同学中选拔一人参加“诵读经典”大赛，在相同的测试条件下，两人 5 次测试成绩（单位：分）如下：
甲：79，86，82，85，83；
乙：88，81，85，81，80．
回答下列问题：
（1）甲成绩的中位数是 ，乙成绩的众数是 ；
（2）经计算知 x乙=83，s乙2=465．请你求出甲的方差，并运用学过的统计知识推荐参加比赛的合适人选．

26. 点 P 是平面直角坐标系中的一点且不在坐标轴上，过点 P 向 x 轴，y 轴作垂线段，若垂线段的长度的和为 4，则点 P 叫做“垂距点”，例如：如图中的 P1,3 是“垂距点”．
（1）在点 A2,2，B32,−52，C−1,5 是“垂距点”的为 ．
（2）若 D32m,12m 为“垂距点”，求 m 的值．
（3）若过点 2,3 的一次函数 y=kx+bk≠0 的图象上存在“垂距点”，则 k 的取值范围是 ．

27. 如图，在 △ABC 中，∠A=90∘，AB=AC，D 为 BC 的中点，E，F 分别是 AB，AC 上的点，且 BE=AF，求证：△DEF 为等腰直角三角形．

28. 在平面直角坐标系 xOy 中，已知点 Ma,b．如果存在点 Naʹ,bʹ，满足 aʹ=∣a+b∣，bʹ=∣a−b∣，则称点 N 为点 M 的“控变点”．
（1）点 A−1,2 的“控变点”B 的坐标为 ；
（2）已知点 Cm,−1 的“控变点”D 的坐标为 4,n，求 m，n 的值；
（3）长方形 EFGH 的顶点坐标分别为 1,1，5,1，5,4，1,4．如果点 Px,−2x 的“控变点”Q 在长方形 EFGH 的内部，直接写出 x 的取值范围．
答案
第一部分
1. B
2. B【解析】可借助图形解决，也可总结出一般规律：这四个点的坐标，每个数字都在相同位置出现两次．
3. D
4. B
5. B
【解析】将方程 4x2+12x−1147=0 两边同除以 4，
得 x2+3x−11474=0．
用配方法解得 x1=312，x2=−372．
∵ a>b，
∴ a=312，b=−372，
∴ 3a+b=28．
6. A
7. D【解析】选项A不是中心对称图形，是轴对称图形；选项B既不是中心对称图形也不是轴对称图形；选项C是中心对称图形，不是轴对称图形；选项D既是中心对称图形也是轴对称图形．
8. B【解析】∵AB∥CD，
∴∠C=∠ABC=30∘，
又 ∵CD=CE，
∴∠D=∠CED，
∵∠C+∠D+∠CED=180∘，即 30∘+2∠D=180∘，
∴∠D=75∘．
故选B．
第二部分
9. −2,−2
【解析】“卒”的坐标为 −2,−2．
10. 6
11. n≥0
【解析】∵ 关于 x 的一元二次方程 x+22=n 有实数根，
而 x+22≥0，
∴n≥0，
故答案为：n≥0．
12. >0，<0
13. −5
【解析】把 x=m 代入方程 x2−2x−5=0 得：m2−2m−5=0，
∴m2−2m=5，
∴2m−m2=−5．
14. 700
15. 4
【解析】在 △ABC 中，∠ACB=90∘，
∴AC=AB2−BC2=132−122=5，
∴AD=AC=5，
∴BD=AB−AD=13−5=8，
∵AC=AD，AE⊥CD，
∴CE=DE，
∵CE=DE，CF=BF，
∴EF 是 △CBD 的中位线，
∴EF=12BD=4．
16. 5700，4900，4800，经理或副经理
第三部分
17. 方程化为
x2−4x+4=0,x−22=0,x1=x2=2.
18. ∵ 四边形 ABCD 是平行四边形，
∴AB∥CD，AO=CO，
∴BE∥DF．
∴∠AEO=∠CFO．
在 △OAE 和 △OCF 中，
∠AEO=∠CFO,∠AOE=∠COF,AO=CO,
∴△OAE≌△OCF．
∴OE=OF．
19. （1） 依题意，得 Δ=−2m+12−4×1×m2=4m+1≥0，
解得 m≥−14．
（2） 答案不唯一，如：m=0，
此时方程为 x2−x=0，
解得 x1=0，x2=1．
20. ∵S△AOB=12⋅AO⋅BC=15，
∴BC=2×156=5，
∴B−4,5，
故 AB：y=52x+15，OB：y=−54x．
21. AE∥CF，AE=CF．
理由如下：
∵ 四边形 ABCD 是平行四边形，
∴AO=CO，BO=DO，
∵ 点 E 是 DO 的中点，点 F 是 BO 的中点，
∴OE=12DO，OF=12BO，
∴OE=OF，
∴ 四边形 AFCE 是平行四边形（对角线互相平分的四边形是平行四边形），
∴AE∥CF，AE=CF．
22. （1） ∵b2−4ac=−4m+22−4m3m+6=16m2+16m+4−12m2−24m=4m2−8m+4=4m−12≥0,
∴ 关于 x 的一元二次方程 mx2−4m+2x+3m+6=0 一定有实数根．
（2） ∵ 无论 m 为何值，该方程都有一个固定的实数根，且 mx2−4x+3−2x+6=0，
∴x2−4x+3=0，且 −2x+6=0，
解得 x=3，
∴ 无论 m 为何值，该方程都有一个固定的实数根，这个根为 3．
23. 如图所示，连接 AC．
因为 AB:BC:CD:DA=2:2:3:1，
所以设 AB=2x，BC=2x，CD=3x，DA=x．
在 Rt△ABC 中，由 AB=BC，得 ∠BAC=45∘，
AC2=AB2+BC2=2x2+2x2=8x2．
所以 AD2+AC2=x2+8x2=9x2．
又因为 DC2=3x2=9x2，
所以 DC2=AD2+AC2．
所以 ∠DAC=90∘．
所以 ∠DAB=∠DAC+∠BAC=90∘+45∘=135∘．
24. （1） A−1,m 是直线 y=−x+2 上的一点，
∴ 将 −1,m 代入 y=−x+2，
m=1+2=3，
∴A−1,3，
将 A−1,3 向右平移 4 个单位长度，得到 B3,3．
（2） 直线 l:y=kx−2k≠0，
当 x>0 时，
y=−2，
∴ 可知 l 必过定点 0,−2，记作点 C，
当 l 过 A 点时，
−1,3 代入 y=kx−2，
3=−k−2，
∴k=−5，
y=−5x−2．
当 l 过点 B 时，
3,3 代入 y=kx−2，
3=3k−2，
∴k=53，
y=53x−2．
一次函数 y=kx+b：∣k∣ 越大，直线与 x 轴的夹角越大，
∴ 根据图象，k>53 或 k<−5．
25. （1） 83 分；81 分
【解析】甲成绩的中位数是 83 分，乙成绩的众数是 81 分．
（2） x甲=15×79+82+83+85+86=83，
∴s甲2=15×−42+32+−12+22+02=6，
∵x甲=x乙，s甲2 ∴ 推荐甲去参加比赛．
26. （1） A 和 B
【解析】根据题意，
对于点 A 而言，2+2=4，A 是“垂距点”；
对于点 B 而言，32+−52=4，B 是“垂距点”；
对于点 C 而言，−1+5=6≠4，
∴C 不是“垂距点”．
（2） 根据题意得 32m+12m=4，
①当 m>0 时，则 2m=4，解得 m=2；
②当 m<0 时，则 −2m=4，解得 m=−2．
故 m 的值为 ±2．
（3） k<−32 或 −120
【解析】如图，取 E0,4，F4,0，G−4,0．连接 EF，EG，
在 EF 上取一点 P，作 PM⊥OE 于 M，PN⊥OF 于 N．
则有四边形 PMON 是矩形，可得 PN=OM，PM=EM，
∴PM+PN=OM=EM=4，
∴ 线段 EF 或线段 EG 上的点是“垂距点”，当直线 y=kx+b 与线段 EF 或线段 EG 有交点时，直线 y=kx+b 上存在“垂距点”．
∵ 直线 y=kx+b，经过 A2,3，
∴3=2k+b，
∴b=3−2k，
∴ 直线 y=kx+3−2k，
当直线经过 E0,4 时，k=−12，
当直线经过 F4,0 时，k=−32，
观察图象可知满足条件的 k 的值为 k<−32 或 −120．
27. 如图，连接 AD，
∵AB=AC，∠BAC=90∘，D 为 BC 的中点，
∴∠B=∠C=45∘，∠ADB=∠ADC=90∘，∠BAD=∠DAF=45∘，
∴∠B=∠BAD=45∘，
∴BD=AD，
在 △BDE 和 △ADF 中，
BD=AD,∠B=∠DAF,BE=AF,
∴△BDE≌△ADFSAS，
∴DE=DF，∠BDE=∠ADF，
∵∠BDE+∠ADE=∠ADB=90∘，
∴∠ADF+∠ADE=90∘，即 ∠EDF=90∘，
∴△EDF 为等腰直角三角形．
28. （1） 1,3
【解析】∵∣−1+2∣=1，∣−1−2∣=3，
∴A−1,2 的“控变点”的坐标为 1,3，
故答案为：1,3．
（2） 由题意得：∣m−1∣=4,∣m+1∣=n,
解得 m=5,n=6 或 m=−3,n=2,
即 m=5，n=6 或 m=−3，n=2．
（3） −43【解析】在平面直角坐标系中，画出长方形 EFGH 如下所示：
由题意得：Q∣x−2x∣,∣x+2x∣，即 Q∣x∣,3∣x∣，
要使 Q 在长方形 EFGH 的内部，则 1<∣x∣<5,1<3∣x∣<4,
解得 1<∣x∣<43，
即 −43