

2021年北京大兴区北京市大兴区永华实验学校八年级下期末数学试卷
展开一、选择题(共10小题;共50分)
1. 在平面直角坐标系中,已知点 P2,−3,则点 P 在
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
2. 如图,紫荆花图案绕中心至少旋转 x∘ 后能与原来的图案互相重合,则 x 的值为
A. 36B. 45C. 60D. 72
3. 一个多边形剪去一个角后(剪痕不过任何一个其它顶点),内角和为 1980∘,则原多边形的边数为
A. 11B. 12C. 13D. 11 或 12
4. 下列条件中,能判断四边形是菱形的是
A. 对角线互相垂直且相等的四边形B. 对角线互相垂直的四边形
C. 对角线相等的平行四边形D. 对角线互相平分且垂直的四边形
5. 把方程 x2+8x+7=0 变形为 x+h2=k 的形式应为
A. x+42=−7B. x−42=−7
C. x+42=9D. x−42=9
6. 如图①,在长方形 ABCD 中,动点 P 从点 B 出发,沿 BC,CD,DA 运动至点 A 停止,设点 P 运动的路程为 x,△ABP 的面积为 y,如果 y 与 x 之间的图象如图②所示,则长方形 ABCD 的面积是
A. 10B. 16C. 20D. 36
7. 已知平行四边形 ABCD 的周长为 32,AB=4,则 BC 的长为
A. 4B. 12C. 24D. 28
8. 小明家位于公园的正东 200 m 处,从小明家出发向北走 300 m 就到小华家,若选取小华家为原点,分别以正东,正北方向为 x 轴,y 轴正方向建立平面直角坐标系,规定一个单位长度代表 1 m 长,则公园的坐标是
A. −300,−200B. 200,300
C. −200,−300D. 300,200
9. 在矩形纸片 ABCD 中,AB=6,AD=10.如图所示,折叠纸片,使点 A 落在 BC 边上的 Aʹ 处,折痕为 PQ.当点 Aʹ 在 BC 边上移动时,折痕的端点 P,Q 也随之移动.若限定点 P,Q 分别在 AB,AD 边上移动,则点 Aʹ 在 BC 边上可移动的最大距离为
A. 2B. 4C. 6D. 8
10. 已知某校女子田径队 23 人年龄的平均数和中位数都是 13 岁,但是后来发现其中有一位同学的年龄登记错误,将 14 岁写成 15 岁.经重新计算后,正确的平均数为 a 岁,中位数为 b 岁,则下列结论中正确的是
A. a<13,b=13B. a<13,b<13C. a>13,b<13D. a>13,b=13
二、填空题(共6小题;共30分)
11. 随机从甲、乙两块试验田中各抽取 100 株麦苗测量高度,计算平均数和方差的结果为: x甲=13 , x乙=13 , S甲2=7.5 , S乙2=21.6 ,则小麦长势比较整齐的试验田是 (填“甲”或“乙”).
12. 一元二次方程 4xx−2=x−2 的解为 .
13. 已知一次函数 y=kx+b(k,b 为常数且 k≠0)的图象经过点 A0,−2 和点 B1,0,则 k= ,b= .
14. 矩形的性质定理.
(1)矩形的四个角都是 .
(2)矩形的对角线 .
15. 同一温度的华氏度数 y∘F 与摄氏度数 x∘C 之间的函数表达式是 y=95x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 ∘C.
16. 下面是“以线段 AB 为直径作圆”的尺规作图过程.
已知:线段 AB.
求作:以 AB 为直径的 ⊙O.
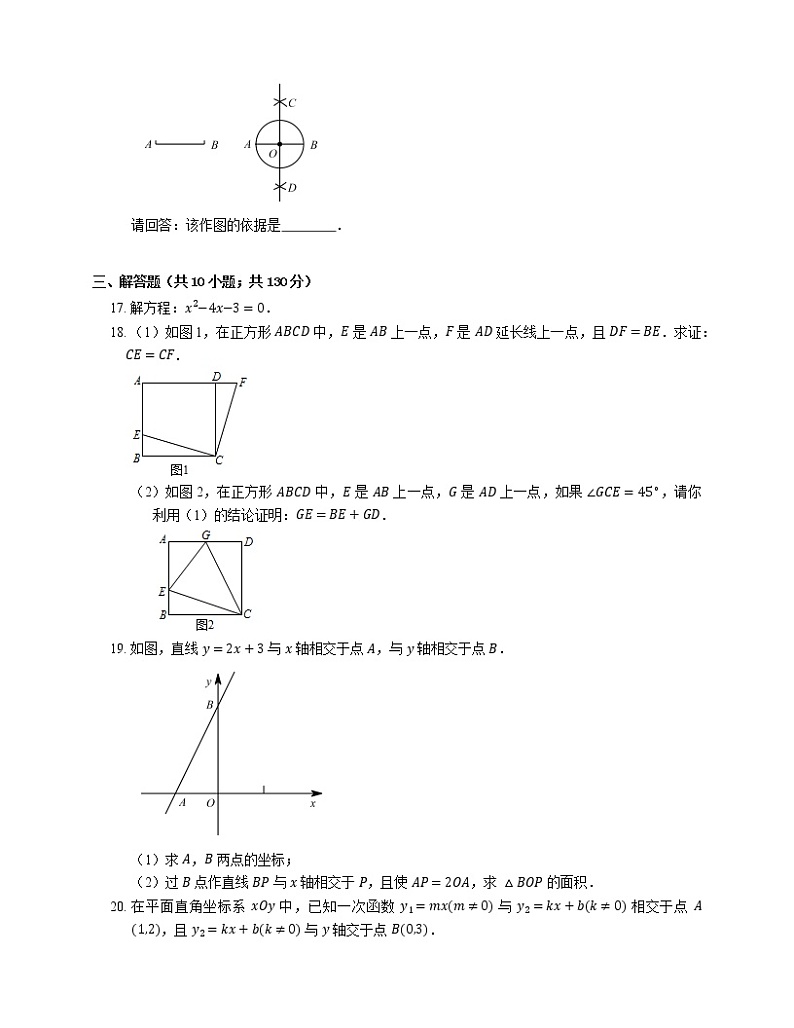
作法:如图,
(1)分别以 A,B 为圆心,大于 12AB 的长为半径作弧,两弧分别相交于点 C 和点 D;
(2)作直线 CD 交 AB 于点 O;
(3)以 O 为圆心,OA 长为半径作圆,则 ⊙O 即为所要求作的图形.
请回答:该作图的依据是 .
三、解答题(共10小题;共130分)
17. 解方程:x2−4x−3=0.
18. (1)如图1,在正方形 ABCD 中,E 是 AB 上一点,F 是 AD 延长线上一点,且 DF=BE.求证:CE=CF.
(2)如图2,在正方形 ABCD 中,E 是 AB 上一点,G 是 AD 上一点,如果 ∠GCE=45∘,请你利用(1)的结论证明:GE=BE+GD.
19. 如图,直线 y=2x+3 与 x 轴相交于点 A,与 y 轴相交于点 B.
(1)求 A,B 两点的坐标;
(2)过 B 点作直线 BP 与 x 轴相交于 P,且使 AP=2OA,求 △BOP 的面积.
20. 在平面直角坐标系 xOy 中,已知一次函数 y1=mxm≠0 与 y2=kx+bk≠0 相交于点 A1,2,且 y2=kx+bk≠0 与 y 轴交于点 B0,3.
(1)求一次函数 y1 和 y2 的解析式;
(2)当 y1>y2>0 时,求出 x 的取值范围.
21. 思思家有一块长 8 m,宽 6 m 的矩形空地,妈妈准备在该空地上建造一个花园,并使花园面积为空地面积的一半,思思设计了如下的四种方案供妈妈挑选,请你选择其中一种方案帮思思求出图中的 x 值.
22. 如图,在平行四边形 ABCD 中,AB=5,AD=10,csB=35,过 BC 的中点 E 作 EF⊥AB,垂足为点 F,连接 DF,求 DF 的长.
23. 已知关于 x 的一元二次方程 x2+bx+c=0.
(1)当 c=b−2 时,利用根的判别式判断方程根的情况;
(2)若方程有两个相等的非零实数根,写出一组满足条件的 b,c 的值,并求此时方程的根.
24. 王大伯几年前承包了甲,乙两片荒山,各栽 100 棵杨梅树,成活 98%,现已挂果,经济效益初步显现.为了分析收成情况,他分别从两山上随意各采摘了 4 棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲,乙两山样本的平均数;
(2)估算出甲,乙两山杨梅的产量总和.
25. 如图 1,已知正方形 ABCD 的对角线 AC,BD 相交于点 O,E 是 AC 上一点,连接 EB,过点 A 作 AM⊥BE,垂足为 M,AM 交 BD 于点 F.
(1)试说明 OE=OF;
(2)如图 2,若点 E 在 AC 的延长线上,AM⊥BE 交 EB 的延长线于点 M,交 DB 的延长线于点 F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.
26. 如图,平面直角坐标系中,直线 y=−3x+3 与 x 轴、 y 轴分别相交于点 B,C.点 A 在第一象限,且 AC⊥y 轴于点 C,AC=3,连接 OA 交 BC 于点 H,连接 AB,点 P 从点 C 出发以每秒 1 个单位长度的速度沿射线 CB 匀速运动,设运动时间为 t 秒.
(1)填空:OB= ,OP+AP 的最小值是 .
(2)当点 P 运动到 BC 中点时,求 OP+AP 的值;
(3)当 OP+AP=4 时,直接写出 t 的值.
答案
第一部分
1. D
2. D
3. B
4. D【解析】A、对角线互相垂直相等的四边形不一定是菱形,此选项错误;
B、对角线互相垂直的四边形不一定是菱形,此选项错误;
C、对角线相等的平行四边形也可能是矩形,此选项错误;
D、对角线互相平分且垂直的四边形是菱形,此选项正确;
故选:D.
5. C
【解析】∵x2+8x+7=0,
∴x2+8x+16=9,
∴x+42=9.
6. C【解析】∵ 动点 P 从点 B 出发,沿 BC,CD,DA 运动至点 A 停止,而当点 P 运动到点 C,D 之间时,△ABP 的面积不变,函数图象上横轴表示点 P 运动的路程,x=4 时,y 开始不变,说明 BC=4,x=9 时,接着变化,说明 CD=9−4=5,
∵ 四边形 ABCD 是矩形,
∴AB=5,BC=4,
∴ 长方形 ABCD 的面积是:4×5=20.
故选C.
7. B
8. C【解析】以小华家为原点,分别以正东,正北方向为 x 轴,y 轴正方向建立平面直角坐标系,
小明家位于小华家正南方 300 m,小明家的坐标为 0,−300,
公园位于小明家正西方 200 m,公园的坐标是 −200,−300.
9. B
10. A
第二部分
11. 甲
12. x1=2,x2=14
【解析】4xx−2=x−2,
4xx−2−x−2=0,
x−24x−1=0,
x−2=0 或 4x−1=0.
解得 x1=2,x2=14.
13. 2,−2
14. 直角,相等
15. −40
【解析】根据题意得 95x+32=x,
解得 x=−40.
16. 到线段两端距离相等的点在线段垂直平分线上;两点确定一条直线;同圆半径相等,且圆心到圆周上点的距离相等
第三部分
17. 移项得
x2−4x=3.
配方得
x2−4x+4=3+4.
即
x−22=7.
开方得
x−2=±7.
∴x1=2+7,x2=2−7.
18. (1) 如图,在正方形 ABCD 中,
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF.
∴CE=CF.
(2) 如图,延长 AD 至 F,使 DF=BE,连接 CF.
由(1)知 △CBE≌△CDF.
∴∠BCE=∠DCF.
∴∠BCE+∠ECD=∠DCF+∠ECD,即 ∠ECF=∠BCD=90∘.
又 ∠GCE=45∘,
∴∠GCF=∠GCE=45∘.
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG.
∴GE=GF.
∴GE=DF+GD=BE+GD.
19. (1) 当 y=0 时,2x+3=0,
解得 x=−32,
则 A 点坐标为 −32,0;
当 x=0 时,y=2x+3=3,
则 B 点坐标为 0,3.
(2) 当点 P 在 x 轴的正半轴上,如图1,
因为 AP=2OA,
所以 OA=OP,
所以 P 点坐标为 32,0,
所以 △BOP 的面积 =12×32×3=94;
当点 P 在 x 轴的负半轴上,如图2,
因为 AP=2OA,
所以 OP=3OA=3×32=92,
所以 P 点坐标为 −92,0,
所以 △BOP 的面积 =12×92×3=274,
综上所述,△BOP 的面积为 94 或 274.
20. (1) ∵ 一次函数 y1=mxm≠0 过点 A1,2,
∴2=m,
∴y1=2x,
又 ∵ 一次函数 y2=kx+bk≠0 经过点 A1,2,B0,3,
∴2=k+b,3=b.
解得:k=−1,b=3.
∴y2=−x+3.
(2) 1
方案一:根据题意,得 8−x6−x=12×8×6,
解得 x1=12,x2=2.x1 不合题意,舍去.
所以 x=2.
【解析】方案二:根据题意,得 8−2x6−2x=12×8×6,
解得 x1=6,x2=1.
∵x1=6 不合题意,
∴ 舍去.
∴x=1.
方案三:根据题意,得 8×6−12×8−x6−x×2=12×8×6,
解得 x1=12,x2=2.
∵x1=12 不合题意,
∴ 舍去,
∴x=2.
方案四:根据题意,得 128−2x+8×6−x=12×8×6,
解得 x1=12,x2=2.
∵x1=12 不合题意,
∴ 舍去,
∴x=2.
22. 延长 DC,FE 相交于点 H.
∵ 四边形 ABCD 是平行四边形,
∴AB∥DC,AB=CD,AD=BC.
∴∠B=∠ECH,∠BFE=∠H.
∵AB=5,AD=10,
∴BC=10,CD=5.
∵E 是 BC 的中点,
∴BE=EC=12BC=5.
∴△BFE≌△CHE.
∴CH=BF,EF=EH.
∵EF⊥AB,
∴∠BFE=∠H=90∘.
在 Rt△BFE 中,
∵csB=BFBE=35,
∴BF=CH=3.
∴EF=BE2−BF2=4,DH=8.
在 Rt△FHD 中,∠H=90∘,
∴DF2=FH2+DH2=82+82=2×82.
∴DF=82.
23. (1) ∵c=b−2,
∴Δ=b2−4c=b2−4b−2=b−22+4,
∵b−22>0,
∴Δ=b−22+4>0.
∴Δ>0,
∴ 方程有两个不相等的实数根.
(2) ∵ 方程有两个相等的实数根,
∴Δ=b2−4c=0.
若 b=2,c=1,方程变形为 x2+2x+1=0,解得 x1=x2=−1.
24. (1) x甲=40 千克;x乙=40 千克.
(2) 7840 千克.
25. (1) ∵ 四边形 ABCD 是正方形,
∴ ∠BOE=∠AOF=90∘,OB=OA,
又 ∵ AM⊥BE,
∴ ∠MEA+∠MAE=90∘=∠AFO+∠MAE,
∴ ∠MEA=∠AFO,
在 △BOE 和 △AOF 中,
∠BOE=∠AOF,∠BEO=∠AFO,OB=OA,
∴ △BOE≌△AOF.
∴ OE=OF;
(2) OE=OF 成立;
理由:
∵ 四边形 ABCD 是正方形,
∴ ∠BOE=∠AOF=90∘,OB=OA,
又 ∵ AM⊥BE,
∴ ∠F+∠MBF=90∘=∠E+∠OBE,
又 ∵ ∠MBF=∠OBE,
∴ ∠F=∠E,
在 △BOE 和 △AOF 中,
∠BOE=∠AOF,∠BEO=∠AFO,OB=OA,
∴ △BOE≌△AOF,
∴ OE=OF.
26. (1) 1;23
【解析】因为直线 y=−3x+3 与 x 轴、 y 轴分别相交于点 B,C,
令 x=0,则 y=3,
所以 C0,3,
令 y=0,则 −3x+3=0,
所以 x=1,
所以 B1,0,
所以 OB=1,
因为 AC⊥y 轴于点 C,AC=3,
所以 A3,3,
当点 P 在直线 OA 上时,OP+AP 最小,最小值为 32+32=23.
(2) 如图,过点 P 作 PD⊥AC 于点 D,PE⊥OC 于 E,
因为点 P 是 BC 的中点,且 B1,0,C0,3,
所以 P12,32,
所以 D12,3,PE=12,PD=32,
所以 AD=52,OE=32.
所以 OP+AP=OE2+PE2+PD2+AD2=1+7.
(3) t=6±134.
【解析】因为点 P 是射线 CB 上的点,
设 Pm,−3m+3,
因为 C0,3,
所以 CP=2m=t,
所以 AP=m−22+3m2,OP=m2+3m−12,
因为 OP+AP=4,
所以 m2+3m−12+m−32+3m2=4,
所以 4m2−6m+3+4m2−6m+9=4,
所以 4m2−6m+3=4−4m2−6m+9.
两边平方得,4m2−6m+3=16+4m2−6m+9−84m2−6m+9,
化简得,44m2−6m+9=11,
两边平方整理得,64m2−96m+23=0,
所以 m1=6+138,m2=6−138.
所以 t=2m=6±134.
2023年北京市大兴区初三二模数学试卷: 这是一份2023年北京市大兴区初三二模数学试卷,共4页。
2023北京市大兴区初三一模数学试卷: 这是一份2023北京市大兴区初三一模数学试卷,共22页。试卷主要包含了如图所示的圆柱,其俯视图是,下面的三个问题中都有两个变量,分解因式等内容,欢迎下载使用。
2020-2021学年北京市大兴区八下期中数学试卷: 这是一份2020-2021学年北京市大兴区八下期中数学试卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












