2021年北京顺义区李桥中学八年级下期末数学试卷

这是一份2021年北京顺义区李桥中学八年级下期末数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题；共50分）
1. 用配方法解方程 x2−2x−1=0 时，配方后得到的方程为
A. x+12=0B. x−12=0C. x+12=2D. x−12=2

2. 下列各数中，能使二次根式 2x−3 有意义的是
A. −1B. 0C. 2D. 1

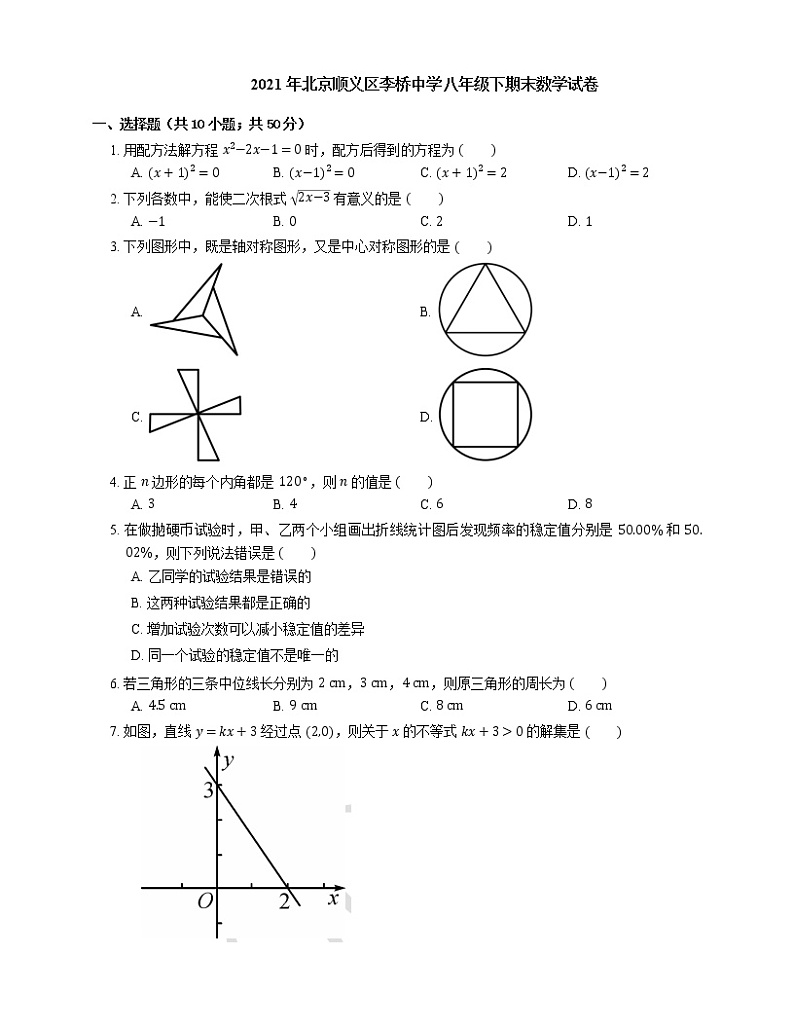
3. 下列图形中，既是轴对称图形，又是中心对称图形的是
A. B.
C. D.

4. 正 n 边形的每个内角都是 120∘，则 n 的值是
A. 3B. 4C. 6D. 8

5. 在做抛硬币试验时，甲、乙两个小组画出折线统计图后发现频率的稳定值分别是 50.00% 和 50.02%，则下列说法错误是
A. 乙同学的试验结果是错误的
B. 这两种试验结果都是正确的
C. 增加试验次数可以减小稳定值的差异
D. 同一个试验的稳定值不是唯一的

6. 若三角形的三条中位线长分别为 2 cm，3 cm，4 cm，则原三角形的周长为
A. 4.5 cmB. 9 cmC. 8 cmD. 6 cm

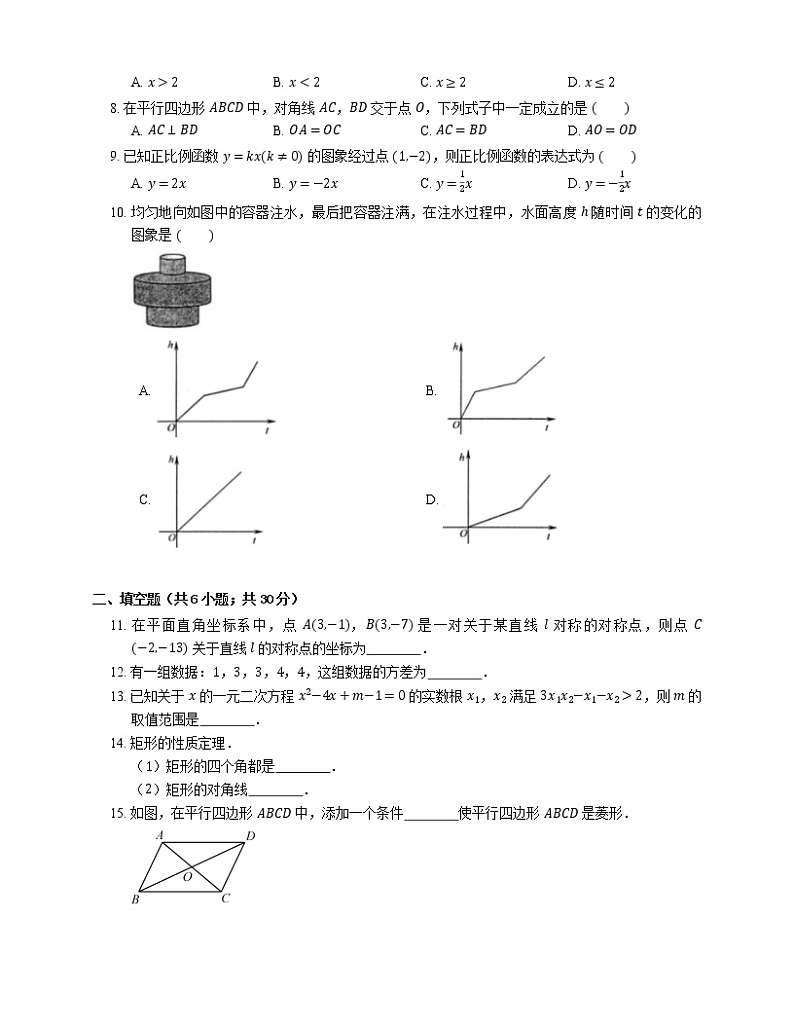
7. 如图，直线 y=kx+3 经过点 2,0，则关于 x 的不等式 kx+3>0 的解集是
A. x>2B. x2，则 m 的取值范围是 ．

14. 矩形的性质定理．
（1）矩形的四个角都是 ．
（2）矩形的对角线 ．

15. 如图，在平行四边形 ABCD 中，添加一个条件 使平行四边形 ABCD 是菱形．

16. 如图，矩形 A1B1C1D1 中，A1B1=3，A1D1=4，顺次连接各边的中点得到四边形 A2B2C2D2；再顺次连接四边形 A2B2C2D2 各边的中点得到四边形 A3B3C3D3；依此类推，则四边形 A2014B2014C2014D2014 的周长是 ．

三、解答题（共9小题；共117分）
17. 解方程：x2−4x−8=0．

18. 如图，在平面直角坐标系中，直线 y=−x+3 经过点 A5,a 且与 y 轴交于点 B，把点 A 向左平移 2 个单位，再向上平移 4 个单位，得到点 C．过点 C 且与直线 y=2x 平行的直线交 y 轴于点 D．
（1）求直线 CD 所对应的函数表达式．
（2）直线 AB 与 CD 相交于点 E，将直线 CD 沿射线 EB 方向平移，平移到经过点 B 的位置结束．设直线 CD 在平移过程中与 x 轴交点的横坐标为 m，求 m 的取值范围．

19. 关于 x 的一元二次方程 x2−2m+1x+m2=0 有两个实数根．
（1）求 m 的取值范围；
（2）写出一个满足条件的 m 的值，并求此时方程的根．

20. 大闸蟹近年产量增加，今年价格是两年前的 910，求这两年价格平均下降的百分率．（参考数据：0.9≈0.95，提示：设两年前价格为单位“1”）

21. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害，为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动．在活动前和活动后分别随机抽取了部分使用电瓶车的市民，就骑电瓶车戴安全帽情况进行问卷调查，将收集的数据制成统计表和如图所示的统计图．
活动前骑电瓶车戴安全帽情况统计表
类别人数A:每次戴68B:经常戴245C:偶尔戴510D:都不戴177合计1000
活动后骑电瓶车戴安全帽情况统计图
（1）宣传活动前，在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
（2）该市约有 30 万人使用电瓶车，请估计活动前全市骑电瓶车“都不戴”安全帽的总人数；
（3）小明认为，宣传活动后骑电瓶车“都不戴”安全帽的人数为 178，比活动前增加了 1 人，因此交警部门开展的宣传活动没有效果．小明分析数据的方法是否合理?请结合统计图表，对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法．

22. （1）如图，平行四边形 ABCD 的对角线 AC，BD 交于点 O．直线 EF 过点 O，分别交 AD，BC 于点 E，F．求证：AE=CF．
（2）如图，将平行四边形 ABCD（纸片）沿过对角线交点 O 的直线 EF 折叠，点 A 落在点 A1 处，点 B 落在点 B1 处．设 FB1 交 CD 于点 G，A1B1 分别交 CD，DE 于点 H，I．求证：EI=FG．

23. 某蒜薹生产基地喜获丰收，收获蒜薹 200 吨，经市场调查，可采用批发、零售、冷库储藏后销售三种方式，并且按这三种方式销售，计划每吨平均的售价及成本如下表：
批发零售储藏后销售销售元/吨300045005500成本元/吨70010001200
若经过一段时间，蒜薹按计划全部售出获得总利润为 y （元 ），蒜薹零售 x （吨 ），且零售量是批发量的 13．
（1）写出 y 与 x 之间的函数关系式；
（2）由于受条件限制，经冷库储藏售出的蒜薹最多为 80 吨，求该生产基地按计划全部售完蒜薹获得的最大利润．

24. 如图，正方形 ABCD 的面积为 16，点 E 是 CD 的中点，点 P 在 BC 上，且 BF=3，求 ∠AEF 的度数．

25. 在平面直角坐标系 xOy 中，对于 P，Q 两点给出如下定义：若点 P 到 x，y 轴的距离中的最大值等于点 Q 到 x，y 轴的距离中的最大值，则称 P，Q 两点为“等距点”．如图中的 P，Q 两点即为“等距点”．
（1）已知点 A 的坐标为 −3,1，
①在点 E0,3，F3,−3，G2,−5 中，为点 A 的“等距点”的是 ；
②若点 B 在直线 y=x+6 上，且 A，B 两点为“等距点”，则点 B 的坐标为 ；
（2）直线 l:y=kx−3k>0 与 x 轴交于点 C，与 y 轴交于点 D．
①若 T1−1,t1，T24,t2 是直线 l 上的两点，且 T1 与 T2 为“等距点”，求 k 的值；
②当 k=1 时，半径为 r 的 ⊙O 上存在一点 M，线段 CD 上存在一点 N，使得 M，N 两点为“等距点”，直接写出 r 的取值范围．
答案
第一部分
1. D【解析】移项，得 x2−2x=1，方程两边同时加上一次项系数一半的平方，得 x2−2x+1=1+1，即 x−12=2．
2. C【解析】由题意得，2x−3≥0，
解得，x≥32，
观察选项，只有选项C符合题意．
故选：C．
3. D【解析】在平面内，把一个图形绕着某个点旋转 180∘，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．
轴对称图形的定义为：平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．直线叫做对称轴．根据轴对称图形的定义可知：
A选项图形不是轴对称图形，也不是中心对称图形，不符合题意，故此选项错误；
B选项图形是轴对称图形，不是中心对称图形，不符合题意，故此选项错误；
C选项图形不是轴对称图形，是中心对称图形，不符合题意，故此选项错误；
D选项图形既是轴对称图形，又是中心对称图形，符合题意，故此选项正确．
4. C
5. A
【解析】A、两试验结果虽然不完全相等，但都是正确的，故错误；
B、两种试验结果都正确，正确；
C、增加试验次数可以减小稳定值的差异，正确；
D、同一个试验的稳定值不是唯一的，正确，故选：A．
6. C
7. B
8. B
9. B【解析】把 1,−2 代入 y=kxk≠0 中，得 k⋅1=−2，即 k=−2，
∴ 此正比例函数的表达式为 y=−2x．故选B．
10. A
第二部分
11. −2,5
12. 1.2
13. 32,
解得 3−3．
依题意可得：
当 −3