2022届高考大一轮复习知识点精练：平面向量数量积的坐标运算

这是一份2022届高考大一轮复习知识点精练：平面向量数量积的坐标运算，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共20小题；共100分）
1. 已知向量 BA=12,32，BC=32,12，则 ∠ABC=
A. 30∘B. 45∘C. 60∘D. 120∘

2. 已知向量 a=1,−1，∣b∣=4，a⋅b=−22，则 a 与 b 的夹角为
A. 5π6B. 3π4C. 2π3D. π3

3. 已知向量 a=4,−2，b=m,2，若 a⊥b，则 m=
A. −1B. 1C. −4D. 4

4. 已知向量 a，b 满足 ∣a∣=1，b=−2,1 ，且 ∣a−b∣=2 ，则 a⋅b=
A. −1B. 0C. 1D. 2

5. 设向量 a 与 b 的夹角为 θ，定义 a 与 b 的“向量积”：a×b 是一个向量，它的模 a×b=a⋅b⋅sinθ，若 a=−3,−1，b=1,3，则 a×b=
A. 3B. 2C. 23D. 4

6. 已知向量 a=λ+2,λ，b=λ,1，若 a⊥b，则实数 λ 的值为
A. 0 或 3B. −3 或 0C. 3D. −3

7. 在平面直角坐标系 xOy 中，已知四边形 ABCD 是平行四边形，AB=1,−2，AD=2,1，则 AD⋅AC=
A. 2B. 3C. 4D. 5

8. 已知向量 m=1,λ+1，n=λ+2,2，若 m⊥n，则 λ=
A. −1B. 0C. −43D. −2

9. 已知向量 a，b，∣a∣=2，∣b∣=csα,sinαα∈R，若 ∣a+2b∣=23，则 a 与 b 夹角是
A. 5π6B. 2π3C. π3D. π6

10. 已知向量 a=32,1，b=−12,4，则
A. a∥a−bB. a⊥a−b
C. a−b∥a+bD. a−b⊥a+b

11. 已知两点 M−1,0，N1,0，若直线 3x−4y+m=0 上存在点 P 满足 PM⋅PN=0，则实数 m 的取值范围是
A. −∞,−5∪5,+∞B. −∞,−25∪25,+∞
C. −25,25D. −5,5

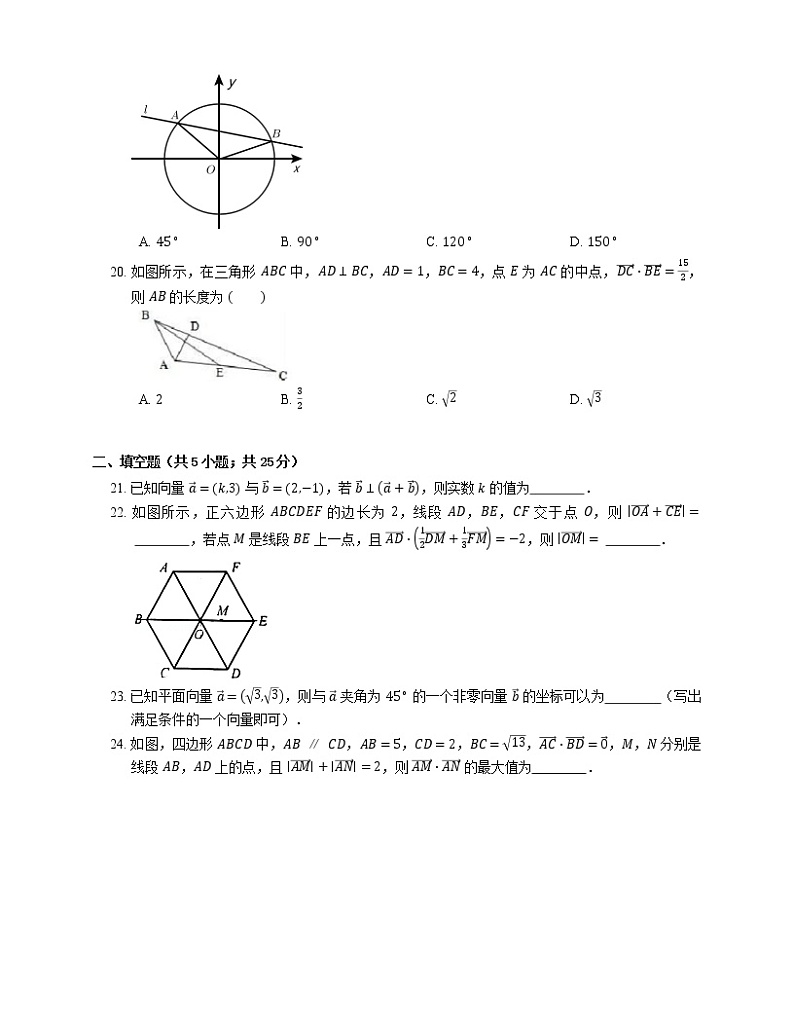
12. 如图所示，在三角形 ABC 中，AD⊥BC，AD=1，BC=4，点 E 为 AC 的中点，DC⋅BE=152，则 AB 的长度为
A. 2B. 32C. 2D. 3

13. 设向量 a=x−2,2，b=4,y，c=x,y，x,y∈R，若 a⊥b，则 ∣c∣ 的最小值是
A. 255B. 455C. 2D. 5

14. 在梯形 ABCD 中，AB∥DC，AB⊥AD，AD=DC=1，AB=2，若 AP=16AD+56AB，则 ∣BC+tPB∣t∈R 的取值范围是
A. 55,+∞B. 2,+∞C. 55,1D. 1,+∞

15. 已知 △ABC 是边长为 2 的等边三角形，P 为平面 ABC 内一点，则 PA⋅PB+PC 的最小值是
A. −2B. −32C. −43D. −1

16. 设 π20，△DBF1 的面积为 1+22．
（1）过点 B 作斜率为 k 的直线 l 交曲线 τ 于 P，Q 两点（异于 B 点），点 P 在第一象限，设点 P 的横坐标为 xP，Q 的横坐标为 xQ，求证：xP⋅xQ 是定值；
（2）过点 F2 的直线 n 与曲线 τ 有且仅有一个公共点，求直线 n 的倾斜角范围；
（3）过点 B 作斜率为 k 的直线 l 交曲线 τ 于 P，Q 两点（异于 B 点），点 P 在第一象限，当 F1P⋅F1Q=3+22 时，求 ∣AP∣=λ∣AQ∣ 成立时 λ 的值．
答案
第一部分
1. A【解析】由两向量的夹角公式，可得 cs∠ABC=BA⋅BCBA⋅BC=12×32+32×121×1=32，则 ∠ABC=30∘．
2. C【解析】根据题意，设 a 与 b 的夹角为 θ，
若向量 a=1,−1，则 ∣a∣=2，
又由 a⋅b=−22，则有 a⋅b=42csθ=−22,变形可得csθ=−12，
又由 0≤θ≤π，则 θ=2π3．
3. B【解析】根据题意，a=4,−2，b=m,2，
若 a⊥b，
则 a⋅b=4m−4=0，
解可得 m=1．
4. C
5. B
【解析】设 a=−3,−1，b=1,3 的夹角为 θ，
则 csθ=−3−32×2=−32，
所以 sinθ=12，
所以 a×b=a⋅b⋅sinθ=2×2×12=2．
6. B【解析】因为 a⊥b，
所以 a⋅b=λ+2λ+λ=0，
即 λλ+3=0，解得 λ=−3或0．
7. D
8. C【解析】因为 m=1,λ+1，n=λ+2,2，
所以若 m⊥n，
所以 m⋅n=λ+2+2λ+1=0，
解得 λ=−43，
故选C．
9. C【解析】由题意可得 ∣b∣=1，
因为 ∣a+2b∣=23，
所以 a2+4a⋅b+4b2=12，
即 8+4a⋅b=12，
所以 a⋅b=1，
设向量 a 与 b 夹角 θ，
所以 csθ=a⋅b∣a∣∣b∣=12，
因为 θ∈0,π，
所以 θ=π3．
10. B
【解析】因为向量 a=32,1，b=−12,4，
所以 a−b=2,−3，
故 a 和 a−b 不共线，故A错误；
因为 a⋅a−b=32×2+1×−3=0，故 a⊥a−b，故B正确；
因为 a+b=1,5，
因为 21≠−35，故 a−b 和 a+b 不平行，故C错误；
因为 a−b⋅a+b=2×1+−3×5≠0，故 a−b 和 a+b 不垂直，故D错误．
11. D【解析】设 Px,y，则 PM=−1−x,−y，PN=1−x,−y，
PM⋅PN=x2−1+y2=x2−1+1169x2+6mx+m2=2516x2+38mx+116m2−1,
由题意知，方程 25x2+6mx+m2−16=0 有解，
所以 Δ=36m2−4×25m2−16≥0，
所以 m2≤25，
所以 −5≤m≤5．
12. C【解析】以 D 为原点，分别以 BC，AD 所在直线为 x，y 轴，建立如图所示平面直角坐标系，
设 BD=x，CD=4−x，则：D0,0，A0,−1，B−x,0，C4−x,0，E4−x2,−12；
所以 DC=4−x,0，BE=4+x2,−12；
所以 DC⋅BE=16−x22+0=152；
因为 x>0，所以解得 x=1；
所以 B−1,0，又 A0,−1；
所以 ∣AB∣=1+1=2．
13. B【解析】由 a⊥b 得 a⋅b=x−2,2⋅4,y=4x−8+2y=0，即 2x+y−4=0，
所以 ∣c∣ 的最小值即为原点到直线 2x+y−4=0 的距离，即 ∣c∣min=∣0+0−4∣22+12=455．
14. A【解析】以 A 点为原点，以直线 AB 为 x 轴，直线 AD 为 y 轴，建立如图所示的直角坐标系，
则 A0,0，B2,0，D0,1，C1,1．
所以 AD=0,1，AB=2,0，BC=−1,1．
设 P 点坐标为 x,y，
则 AP=x,y，
因为 AP=16AD+56AB，
所以 x,y=160,1+562,0=53,16，
所以 PB=13,−16，
所以 BC+tPB=t3−1,1−t6，
所以 ∣BC+tPB∣2=t3−12+1−t62=536t2−t+2，
设 ft=536t2−t+2，则对称轴为 t=185，
当 t=185 时，ftmin=f185=15，
所以 ∣BC+tPB∣t∈R 的取值范围是 55,+∞．
15. B
【解析】建立如图所示的坐标系，
以 BC 中点为坐标原点，则 A0,3，B−1,0，C1,0，设 Px,y，则 PA=−x,3−y，PB=−1−x,−y，PC=1−x,−y，则
PA⋅PB+PC=2x2−23y+2y2=2x2+y−322−34,
所以当 x=0，y=32 时，取得最小值 2×−34=−32．
16. C
17. C【解析】由题意可知，抛物线 C 的焦点 Fp2,0，
设点 A0,2，抛物线 C 上点 Mx0,y0，
则 AF=p2,−2，AM=y022p,y0−2，
由已知得，AF⋅AM=0，即 y02−8y0+16=0，
解得 y0=4，M8p,4．
由 ∣MF∣=5，得 8p−p22+16=5．
又 p>0，解得 p=2 或 p=8，则抛物线 C 的方程为 y2=4x 或 y2=16x．
故选C．
18. D【解析】以 AʹBʹ，AʹDʹ 为 x，y 轴建系，令 ∠AʹAD=θ，
由于 AD=1，故 AʹA=csθ，AʹD=sinθ，
如图，
∠BABʹ=π2−θ，AB=1，
故 xB=csθ+csπ2−θ=csθ+sinθ，yB=sinπ2−θ=csθ，
故 AʹB=csθ+sinθ,csθ，
同理可得 Csinθ,csθ+sinθ，
即 AʹC=sinθ,csθ+sinθ，
所以 AʹB⋅AʹC=csθ+sinθ,csθ⋅sinθ,csθ+sinθ=1+sin2θ，
当 θ=π4 时，故 AʹB⋅AʹC 的最大值为 2．
19. C【解析】圆 O:x2+y2=4 的圆心为 O0,0，半径 R=2，
所以 OA=OB=2，
因为 OA⋅OB=OAOBcsOA,OB=4csOA,OB=−2，
所以 csOA,OB=−12，
所以 OA 和 OB 的夹角为 120∘．
20. C
【解析】以 D 为原点，分别以 BC，AD 所在直线为 x，y 轴，建立如图所示平面直角坐标系，
设 BD=x，CD=4−x，则：D0,0，A0,−1，B−x,0，C4−x,0，E4−x2,−12；
所以 DC=4−x,0，BE=4+x2,−12；
所以 DC⋅BE=16−x22+0=152；
因为 x>0，
所以解得 x=1，
所以 B−1,0，
又 A0,−1，
所以 ∣AB∣=1+1=2．
第二部分
21. −1
【解析】因为向量 a=k,3 与 b=2,−1，若 b⊥a+b，
则 b⋅a+b=a⋅b+b2=2k−3+5=0，
求得实数 k=−1．
22. 4，25
【解析】以 O 为坐标原点，建立平面直角坐标系如图，
则 A−1,3，C−1,−3，E2,0，F1,3，D1,−3，
所以 OA=A−1,3，CE=3,3，
所以 OA+CE=2,23，则 OA+CE=22+232=4；
AD=2,−23，设 Ma,0−2≤a≤2，
12DM=a−12,32，13FM=a−13,−33，
由 AD⋅12DM+13FM=−2，得 2,−23⋅5a−16,36=53a−1−1=0，
即 a=25．
所以 M25,0，则 OM=25．
23. 1,0
【解析】只要答 a,0 或 0,b，a>0，b>0 都可以．
24. 12
25. −1,2
第三部分
26. x 的取值范围是 x>−103 且 x≠65．
27. （1） 设 z=x+yix,y∈R，
则 x2+y2=2,2xy=2⇒x=y=1 或 x=y=−1，
所以 z=1+i 或 z=−1−i．
（2） 当 z=1+i 时，z2=2i，z−z2=1−i，
所以 A1,1，B0,2，C1,−1，
所以 OA+OB⋅OC=1,3⋅1,−1=1−3=−2，
当 z=−1−i 时，z2=2i，z−z2=−1−3i，
所以 A−1,−1，B0,2，C−1,−3．
所以 OA+OB⋅OC=−1,1⋅−1,−3=1−3=−2．
28. （1） 因为 a⊥b，
所以 a⋅b=0，
即 a⋅b=csx+3sinx=212csx+32sinx=2sinx+π6=0，
所以 x+π6=kπk∈Z，
因为 x∈π3,π，
所以 x=56π．
（2） a⋅b=abcsπ6=1×2×32=3，
所以 2sinx+π6=3，sinx+π6=32，
因为 x∈π3,π，
所以 x+π6∈π2,7π6，
所以 x+π6=2π3，
所以 x=2π3−π6=π2，
所以 csx=0．
29. （1） 设 c=x,y，
由 c=32 且 c∥a 可得 y+x=0,x2+y2=18.
所以 x=−3,y=3 或 x=3,y=−3.
故 c=−3,3 或 c=3,−3．
（2） 因为 a=2 且 a⊥a−2b，
所以 a⋅a−2b=0，即 a2−2a⋅b=0，
所以 2−2a⋅b=0，
故 csθ=a⋅ba⋅b=22，θ=π4．
30. （1） 因为 OP=2,1，则直线 OP 的方程为 y=12x，
因为 C 是直线 OP 上的一点，则设点 Cx,12x，
所以 CA=OA−OC=1−x,7−12x，CB=OB−OC=5−x,1−12x，
所以 CA⋅CB=1−x5−x+7−12x1−12x=54x2−10x+12=54x−42−8，
所以当 x=4 时，CA⋅CB 取到最小值，此时 C4,2，
所以 OC=4,2．
（2） 由（1）可知，C4,2，
所以 CA=−3,5，CB=1,−1，
所以 cs∠ACB=CA⋅CBCA⋅CB=−3−5−32+5212+−12=−41717，
故 cs∠ACB=−41717．
31. （1） 设直线方程 y=kx−1 与 x2−y2=1y≥0 交点坐标 xP=k2+1k2−1，
设直线方程 y=kx−1 与 x2+y2=1y≤0 交点坐标 xQ=k2−1k2+1，
所以 xPxQ=1．
（2） 根据面积 12×1×1+c=1+22 求出 c=2．
设过点 F2 直线 n 的方程为 y=mx−2，
y=mx−2,x2+y2=1,y≤0, 只有 1 个交点，m=1．
双曲线 x2−y2=1y≥0 的渐近线方程 y=±x，
所以 m>1 或 m≤−1 时，
直线 y=mx−2 只与 x2−y2=1y≥0 有一个交点，
显然直线 m 的方程为 x=2 时也符合题意，
所以直线 m 的倾斜角取值范围为 π4,3π4．
（3） F1P=xP+2,yP；F1Q=xQ+2,yQ
F1P⋅F1Q=xP+2xQ+2+yPyQ=1+k2xPxQ+2−k2xP+xQ+k2+2，
因为 xP+xQ=2k4+4k4−1，xPxQ=1，
所以 F1P⋅F1Q=3+2k2+2−k22k4+2k4−1，
3+2k2+2−k22k4+2k4−1=3+22，
解出 k2=2．
解法一直接法：
xP=3+22，xQ=3−22，
∣AP∣=40+282，∣AQ∣=8−42，
所以 λ=40+2828−42=17+122=3+22．
解法二性质法：
kPA⋅kQA=−1，根据双曲线的性质知道 kPA⋅kQB=yPxP+1⋅yPxP−1=yP2xP2−1=1，
所以 kPA=−kQA，
所以 ∠PAB=∠QAB．
∣AP∣=λ∣AQ∣，λ=∣AP∣∣AQ∣=∣PB∣∣BQ∣=1+k2k2−1−11−k2−1k2+1=k2+1k2−1，
所以 λ=3+22．
解法三整体代入法：
∣AP∣=λ∣AQ∣，
所以 λ=xP+12+2xP−12xQ+12+2xQ−12
=xP+xPxQ2+2xP−xPxQ2xQ+12+2xQ−12=xP2．
又 xP+xQ=6，xPxQ=1，
则 xP，xQ 是方程 x2−6x+1=0 的两个根，
所以 λ=xP=3+22．