2022届高考大一轮复习知识点精练：余弦函数的性质

这是一份2022届高考大一轮复习知识点精练：余弦函数的性质，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共20小题；共100分）
1. 要得到余弦曲线 y=csx，只需将正弦曲线 y=sinx 向左平移
A. π2 个单位B. π3 个单位C. π4 个单位D. π6 个单位

2. 设 α∈−π,π，且 csα=−12，则 α=
A. −2π3 或 2π3B. −π3 或 π3C. −π3 或 2π3D. −2π3 或 π3

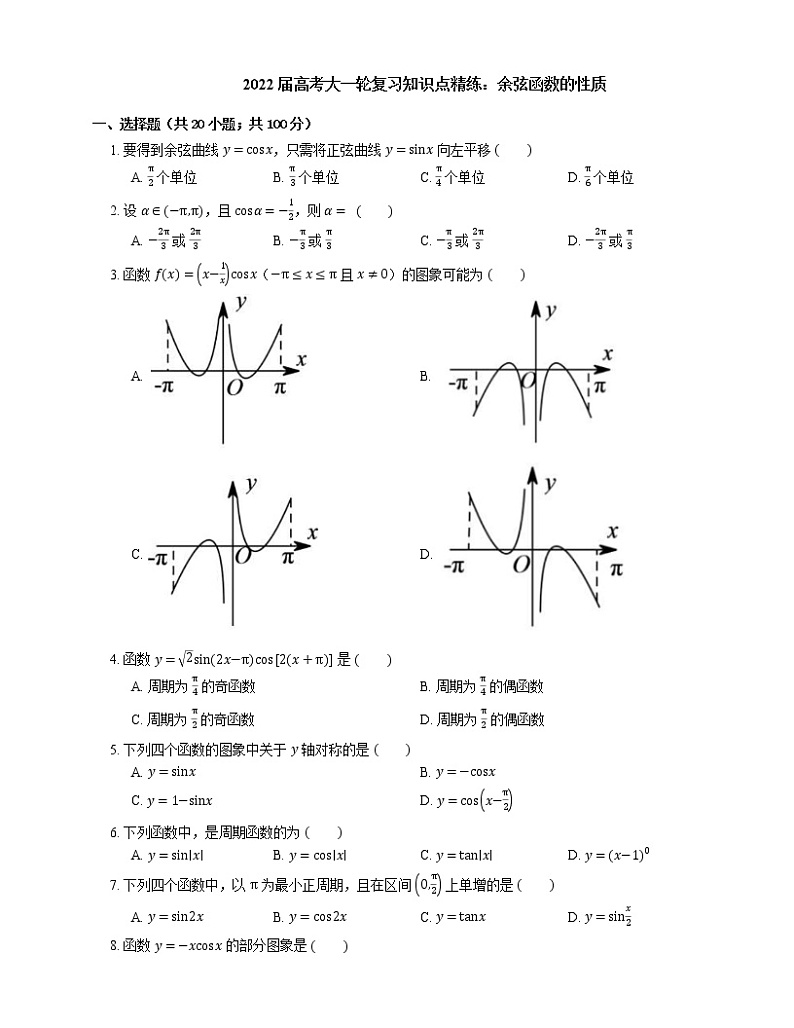
3. 函数 fx=x−1xcsx（−π≤x≤π 且 x≠0）的图象可能为
A. B.
C. D.

4. 函数 y=2sin2x−πcs2x+π 是
A. 周期为 π4 的奇函数B. 周期为 π4 的偶函数
C. 周期为 π2 的奇函数D. 周期为 π2 的偶函数

5. 下列四个函数的图象中关于 y 轴对称的是
A. y=sinxB. y=−csx
C. y=1−sinxD. y=csx−π2

6. 下列函数中，是周期函数的为
A. y=sin∣x∣B. y=cs∣x∣C. y=tan∣x∣D. y=x−10

7. 下列四个函数中，以 π 为最小正周期，且在区间 0,π2 上单增的是
A. y=sin2xB. y=cs2xC. y=tanxD. y=sinx2

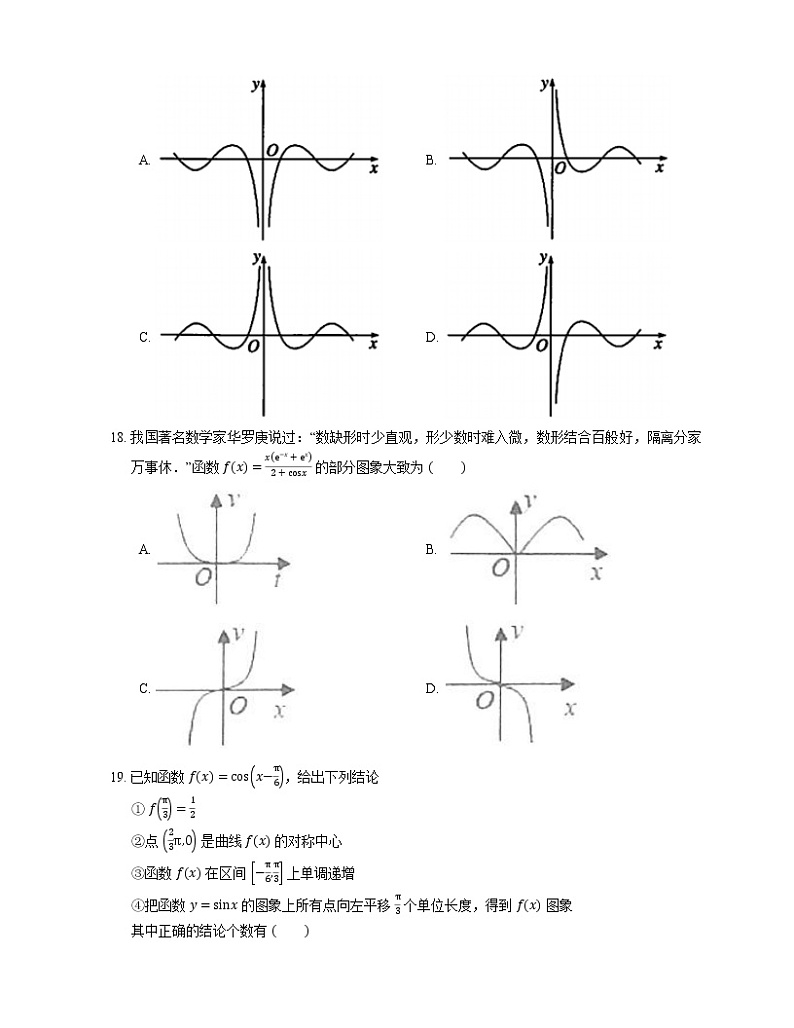
8. 函数 y=−xcsx 的部分图象是
A. B.
C. D.

9. 函数 fx=sin2x+csx x∈0,π2 的最大值为
A. 1B. 54C. 32D. 2

10. y=∣csx∣ 的一个单调递增区间是
A. −π2,π2B. 0,πC. π,3π2D. 3π2,2π

11. 若 32sinx+12csx=4−m，则实数 m 的取值范围是
A. 3≤m≤5B. −5≤m≤5C. 3B”是“cs2A−2π3，使得关于 x 的方程 csx=a 在区间 −2π3,m 内恰有一个解，则 a 的取值范围为 ．

24. 函数 fx=sin2x+3π2−3csx 的最小值为 ．

25. 设 α，β 都是锐角，csα=17，csα+β=5314．请问 csβ 是否可以求解，若能求解，求出答案；若不能求解，简述理由： ．

三、解答题（共6小题；共78分）
26. 求使 y=csx 取得最大值和最小值的 x 的集合．

27. 利用余弦线，研究余弦函数 y=csx 的单调性、最大值和最小值，并分别求出函数取得最大值和最小值时 x 的值．

28. 求函数 fx=−2sin2x+2csx 的最大值和最小值．

29. 已知对任意 x∈R，acsx+bcs2x≥−1 恒成立，求 a+bmax．

30. 已知函数 fx=sin2x+acsx−12 在 0≤x≤π2 上的最大值为 1，求实数 a 的值．

31. 已知函数 fx=csx−π≤x0 时，fx>7．
19. B
20. A
【解析】因为 x∈R，所以 π2x∈R，
所以 y=csπ2x 的值域为 −1,1．
所以 y=1−2csπ2x 的最大值为 3，最小值为 −1．
第二部分
21. −2π,−π，0,π，0
【解析】作出函数 y=csx，x∈−2π,3π2 的图象，如图所示．
观察图象可知函数 y=csx 的单调递减区间有两个：−2π,−π，0,π．
函数 y=csx 的最大值为 1，最小值为 −1．
所以最大值与最小值的和为 0．
22. π
【解析】因为 fx=cs2x，所以 fx 的最小正周期为 T=2π2=π．
23. −1,1
【解析】当 a1 时，方程总是无解．
当 −12≤a≤1 时，存在 m=0，方程 csx=a 在 −2π3,m 内恰有一个解，
当 −1≤a