2021年北京朝阳区立华学校（初中部）九年级上期末数学试卷

这是一份2021年北京朝阳区立华学校（初中部）九年级上期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 抛物线 y=−x2 开口方向是
A. 向上B. 向下C. 向左D. 向右

2. 如图，在平面直角坐标系中，直线 OA 过点 2,1，则 tanα 的值是
A. 55B. 5C. 12D. 2

3. 如图，△ABC中，D、E分别为边AB、AC上的点，且DE∥BC，下列判断错误的是( )
A. ADDB=AEECB. ADDB=DEBCC. ADAB=AEACD. ADAB=DEBC

4. 已知 ∠BAC=45∘，一动点 O 在射线 AB 上运动（点 O 与点 A 不重合），设 OA=x，如果半径为 1 的 ⊙O 与射线 AC 有公共点，那么 x 的取值范围是
A. 02

5. 用幻灯机将一个三角形的面积放大为原来的 16 倍，则下列说法中正确的是
A. 放大后，∠A，∠B，∠C 是原来的 16 倍
B. 放大后周长是原来的 4 倍
C. 放大后对应边长是原来的 16 倍
D. 放大后对应中线长是原来的 16 倍

6. 如图，四边形 ABCD 内接于 ⊙O，∠BCD=130∘，则 ∠BAD 的度数是
A. 30∘B. 50∘C. 65∘D. 100∘

7. 若反比例函数 y=1x 的图象上有两点 P11,y1 和 P22,y2，那么
A. y2y2>0C. y2>y1>0D. y1
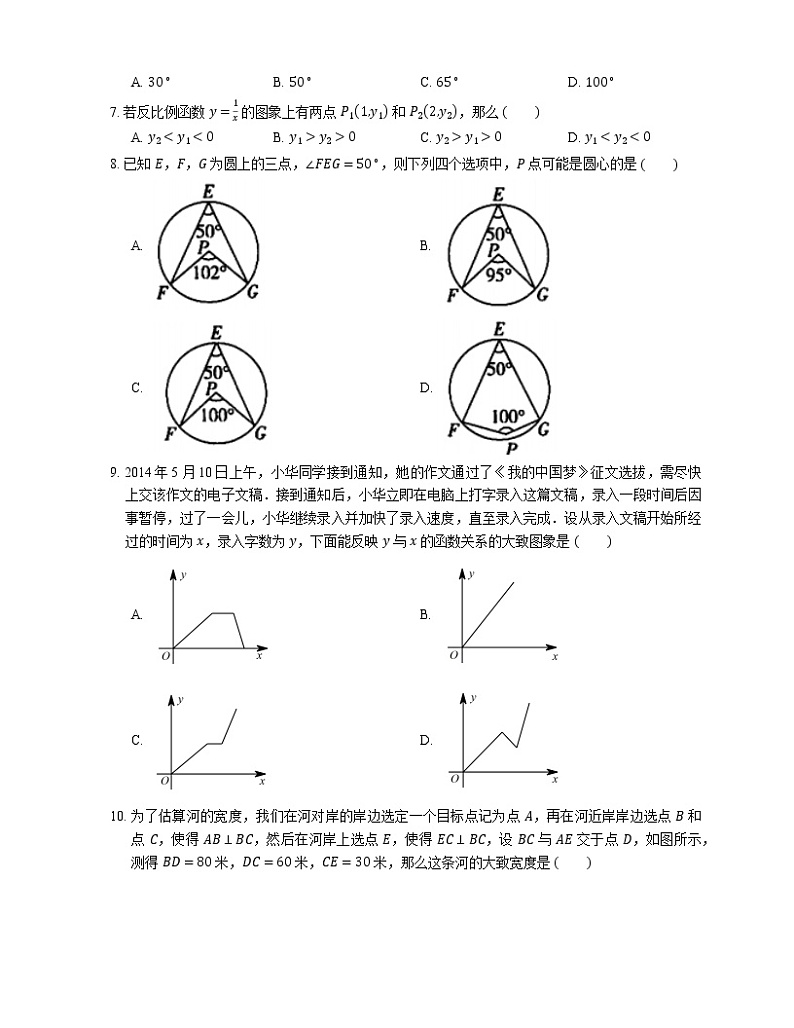
8. 已知 E，F，G 为圆上的三点，∠FEG=50∘，则下列四个选项中，P 点可能是圆心的是
A. B.
C. D.

9. 2014年5月10日上午，小华同学接到通知，她的作文通过了《我的中国梦》征文选拔，需尽快上交该作文的电子文稿．接到通知后，小华立即在电脑上打字录入这篇文稿，录入一段时间后因事暂停，过了一会儿，小华继续录入并加快了录入速度，直至录入完成．设从录入文稿开始所经过的时间为 x，录入字数为 y，下面能反映 y 与 x 的函数关系的大致图象是
A. B.
C. D.

10. 为了估算河的宽度，我们在河对岸的岸边选定一个目标点记为点 A，再在河近岸岸边选点 B 和点 C，使得 AB⊥BC，然后在河岸上选点 E，使得 EC⊥BC，设 BC 与 AE 交于点 D，如图所示，测得 BD=80 米，DC=60 米，CE=30 米，那么这条河的大致宽度是
A. 25 米B. 30 米C. 40 米D. 50 米

二、填空题（共6小题；共30分）
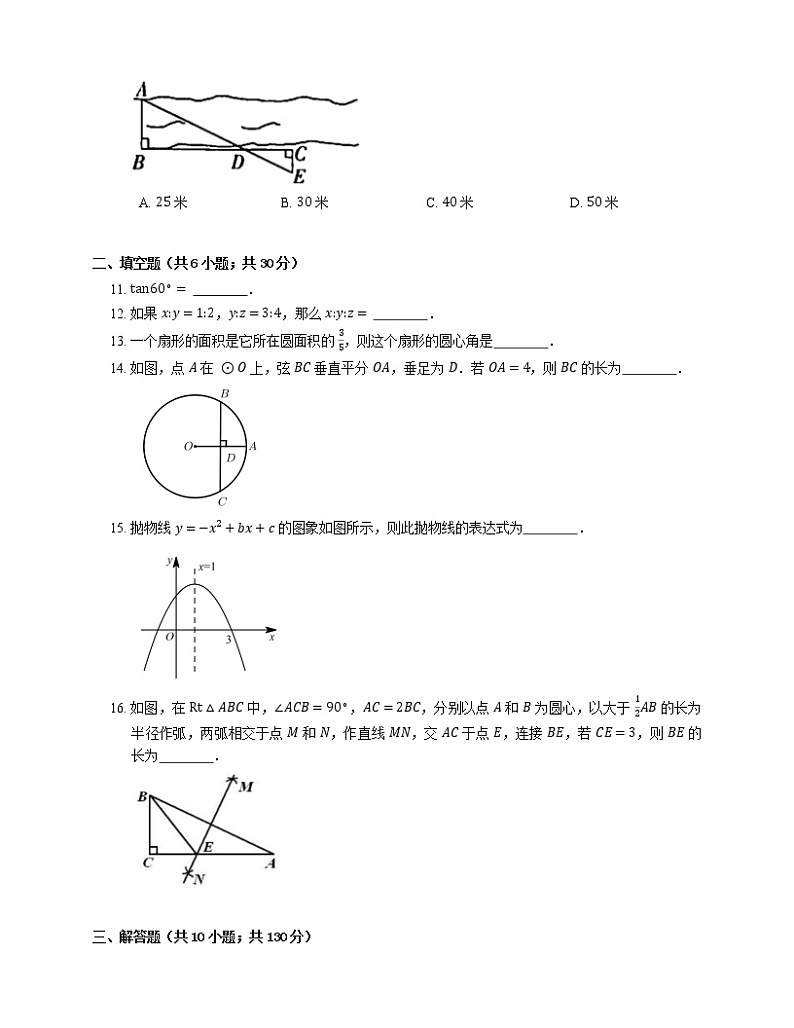
11. tan60∘= ．

12. 如果 x:y=1:2，y:z=3:4，那么 x:y:z= ．

13. 一个扇形的面积是它所在圆面积的 35，则这个扇形的圆心角是 ．

14. 如图，点 A 在 ⊙O 上，弦 BC 垂直平分 OA，垂足为 D．若 OA=4，则 BC 的长为 ．

15. 抛物线 y=−x2+bx+c 的图象如图所示，则此抛物线的表达式为 ．

16. 如图，在 Rt△ABC 中，∠ACB=90∘，AC=2BC，分别以点 A 和 B 为圆心，以大于 12AB 的长为半径作弧，两弧相交于点 M 和 N，作直线 MN，交 AC 于点 E，连接 BE，若 CE=3，则 BE 的长为 ．

三、解答题（共10小题；共130分）
17. 用含 30∘，45∘，60∘ 这三个特殊角的四个三角比及其组合可以表示某些实数，如：12 可表示为 12=sin30∘=cs60∘=tan45∘⋅sin30∘=⋯．
仿照上述材料，完成下列问题
（1）用含 30∘，45∘，60∘ 这三个特殊角的三角比或其组合表示 32，即：
填空：32= = = =⋯；
（2）用含 30∘，45∘，60∘ 这三个特殊角的三角比，结合加、减、乘、除四种运算，设计一个等式．要求：等式中须含有这三个特殊角的三角比、上述四种运算都至少出现一次，且这个等式的结果等于 1．即：
填空：1= ．

18. 已知抛物线 y=ax2+bx+ca≠0 与 y 轴的交点为 C．若自变量 x 和函数值 y 的部分对应值如下表所示：
x⋯−101⋯y⋯1054⋯
（1）求点 C 的坐标；
（2）求 y 与 x 之间的函数关系式．

19. 请回答：
（1）尝试：如图①，已知 A，E，B 三点在同一条直线上，且 ∠A=∠B=∠DEC=90∘，求证：△ADE∽△BEC；
（2）一位同学在尝试了上题后还发现：如图②③，只要 A，E，B 三点在同一条直线上，且 ∠A=∠B=∠DEC，则（1）中的结论总成立．你同意吗?请在图②③中选择一个说明理由．

20. 在平面直角坐标系 xOy 中，已知点 P2,2，Q−1,2，函数 y=mxm≠0．
（1）当函数 y=mxm≠0 的图象经过点 P 时，求 m 的值；
（2）若 P，Q 两点中恰有一个点的坐标满足不等式组 y>mx,y0，求 m 的取值范围．

21. 如图，某山顶上建有手机信号中转塔 AB，在地面 D 处测得塔尖的仰角 ∠ADC=60∘，塔底的仰角 ∠BDC=45∘，点 D 距塔 AB 的距离 DC 为 100 米，求手机信号中转塔 AB 的高度（结果保留根号）．

22. 如图，在以 O 为圆心的两个同心圆中，大圆的弦 AB 交小圆于 C，D 两点．求证：AC=BD．

23. 如图，在 △ABC 中，AB=AC，以 AB 为直径作 ⊙O 交 BC 于点 D，过点 D 作 AC 的垂线交 AC 于点 E，交 AB 的延长线于点 F．
（1）求证：DE 与 ⊙O 相切；
（2）若 CD=BF，AE=3，求 DF 的长．

24. （1）已知一元二次方程 ax2+bx+c=0b2−4ac≥0 的根分别为 x1，x2，求证：x1+x2=ba，x1⋅x2=ca．
（2）已知抛物线 y=ax2+bx+c 的顶点坐标为 1,−9，它与 x 轴有两个交点为 Ax1,0，Bx2,0，且 x12+x22=20，求 a，b，c 的值．

25. 如图，在直角坐标系中有一直角三角形 AOB，O 为坐标原点，OA=1，tan∠BAO=3，将此三角形绕原点 O 逆时针旋转 90∘，得到 △DOC，抛物线 y=ax2+bx+c 经过点 A，B，C．
（1）求抛物线的解析式；
（2）若点 P 是第二象限内抛物线上的动点，其横坐标为 t，
①设抛物线对称轴 l 与 x 轴交于一点 E，连接 PE，交 CD 于 F，求出当 △CEF 与 △COD 相似时，点 P 的坐标；
②是否存在一点 P，使 △PCD 得面积最大?若存在，求出 △PCD 的面积的最大值；若不存在，请说明理由．

26. 如图所示，Rt△ABC 的两条直角边 BC=3，AC=4，斜边 AB 上的高为 CD，以点 C 为圆心作 ⊙C，半径为 r．
（1）当 r 取什么值时，点 D 在 ⊙C 上?
（2）若点 D 在 ⊙C 内，点 A 在 ⊙C 外，求 r 的取值范围．
答案
第一部分
1. B【解析】∵a=−1<0，
∴ 抛物线的开口向下．
2. C
3. B【解析】【分析】如图，证明△ADE∽△ABC，得到ADAB=DEBC=AEAC；证明ADDB=AEEC≠DEBC，即可解决问题．
【解析】解：如图，∵DE∥BC，
∴△ADE∽△ABC，
∴ADAB=DEBC=AEAC，
∴C、D正确．
∵DE∥BC，
∴ADDB=AEEC≠DEBC，
故选：B．
【点评】该题主要考查了平行线分线段成比例定理及其应用问题；观察图形、数形结合，正确写出比例式是解题的关键．
4. C
5. B
6. B
7. B
8. C【解析】若 P 点为圆心，则 ∠FPG=2∠FEG=100∘．
观察C、D易知C符合题意．
9. C
10. C
【解析】∵AB⊥BC，EC⊥BC，
∴∠B=∠C=90∘．
又 ∵∠ADB=∠EDC，
∴△ADB∽△EDC．
∴ABBD=CECD，即 AB80=3060，
解得 AB=40，
∴ 这条河的大致宽度是 40 米．
第二部分
11. 3
12. 3:6:8
13. 216∘
14. 43
【解析】如图所示，连接 OB，
∵ 点 A 在 ⊙O 上，
∴OA 为 ⊙O 的半径，
又弦 BC 垂直平分 OA，垂足为 D，OA=4，
∴OB=OA=4，OD=AD=12OA=2，OA⊥BC，
Rt△OBD 中由勾股定理得：OB2=BD2+OD2，
∴BD=OB2−OD2=42−22=23，
又 OD⊥BC，
∴ 由垂径定理得 BD=CD=12BC，
∴BC=2BD=2×23=43，
故 BC 长为 43．
15. y=−x2+2x+3
16. 5
第三部分
17. （1） sin60∘；cs30∘；tan45∘⋅sin60∘ 等
（2） tan45∘+sin30∘⋅ct45∘−cs60∘÷tan45∘=1 等
18. （1） 由抛物线 y=ax2+bx+c 经过点 0,5，
∴C0,5．
（2） 由已知得 c=5．
∴y=ax2+bx+5．
∵ 点 −1,10，1,4 在抛物线 y=ax2+bx+5 上，
得 a−b+5=10,a+b+5=4,
解得 a=2,b=−3.
∴y 与 x 之间的函数关系式为 y=2x2−3x+5．
19. （1） ∵∠A=∠DEC=90∘，
∴∠DEA+∠CEB=90∘，∠DEA+∠D=90∘，
∴∠D=∠CEB，
又 ∠A=∠B，
∴△ADE∽△BEC．
（2） 同意，选择图②说明理由：
∵∠A=∠DEC，∠A+∠D=∠DEC+∠CEB，
∴∠D=∠CEB，
又 ∠A=∠B，
∴△ADE∽△BEC．
（也可选图③）
20. （1） ∵ 函数 y=mxm≠0 的图象经过点 P2,2，
∴2=m2，即 m=4．
（2） 当点 P2,2 满足 y>mx,y0 时，由不等式组 2>m2,2<2+m 得 0当点 Q−1,2 满足 y>mx,y0 时，由不等式组得 2>−m,2<−1+m 得 m>3．
∵P，Q 两点中恰有一个点的坐标满足 y>mx,y0，
∴m 的取值范围是 021. 由题意可知，△ACD 与 △BCD 都是直角三角形．
在 Rt△BCD 中，
∵∠BDC=45∘，
∴BC=CD=100．
在 Rt△ACD 中，
∵∠ADC=60∘，CD=100，
∴tan∠ADC=ACCD，即 AC100=3．
∴AC=1003．
∴AB=AC−BC=1003−1．
答：手机信号中转塔的高度为 1003−1 米．
22. 过点 O 作 OE⊥AB 于点 E．
∵O 为圆心，且 OE⊥AB．
∴AE=BE，
同理 CE=DE．
∴AC=BD．
23. （1） 连接 OD，
∵ AB 是 ⊙O 的直径，
∴ ∠ADB=90∘，
∴ AD⊥BC，
又 ∵ AB=AC，
∴ ∠1=∠2，
∵ OA=OD，
∴ ∠2=∠ADO，
∴ ∠1=∠ADO，
∴ OD∥AC，
∵ DE⊥AC，
∴ ∠ODF=∠AED=90∘，
∴ OD⊥ED，
∵ OD 过 O，
∴ DE 与 ⊙O 相切．
（2） ∵ AB=AC，AD⊥BC，
∴ ∠1=∠2，CD=BD，
∵ CD=BF，
∴ BF=BD，
∴ ∠3=∠F，
∴ ∠4=∠3+∠F=2∠3，
∵ OB=OD，
∴ ∠ODB=∠4=2∠3，
∵ ∠ODF=90∘，
∴ ∠3=∠F=30∘，∠4=∠ODB=60∘，
∵ ∠ADB=90∘，
∴ ∠2=∠1=30∘，
∴ ∠2=∠F，
∴ DF=AD，
∵ ∠1=30∘，∠AED=90∘，
∴ AD=2ED，
∵ AE2+DE2=AD2，AE=3，
∴ AD=23，
∴ DF=23．
24. （1） ∵ 一元二次方程 ax2+bx+c=0b2−4ac≥0 的根分别为 x1，x2，
∴ax−x1x−x2=0，
∴x2−x1+x2x+x1x2=0．（1）
ax2+bx+c=0 两边同时除以 a，得 x2+bax+ca=0，（2）
比较（1）（2）可得，x1+x2=−ba，x1⋅x2=ca．
（2） ∵ 抛物线 y=ax2+bx+c 的顶点坐标为 1,−9，
∴y=ax−12−9=ax2−2ax+a−9．
令 ax2−2ax+a−9=0，则由（1）得 x1+x2=2，x1⋅x2=a−9a．
∵x12+x22=20，
∴x1+x22−2x1x2=20．
∴4−2×a−9a=20，解得 a=1．
经检验，a=1 是上述分式方程的解．
∵−b2a=1，
∴b=−2．
∵4ac−b24a=−9，
∴c=−8．
25. （1） ∵OA=1．tan∠BAO=3，
∴OBOA=3，解得 OB=3，
又由旋转可得 OB=OC=3，
∴A1,0，B0,3，C−3,0，
设抛物线解析式为 y=ax2+bx+c，把 A，B，C 三点的坐标代入可得
a+b+c=0,9a−3b+c=0,c=3.，解得 a=−1,b=−2,c=3.
∴ 抛物线解析式为 y=−x2−2x+3．
（2） ①由（1）可知抛物线对称轴为 x=−1，顶点坐标为 −1,4，
∵△COD 为直角三角形，
∴ 当 △CEF 与 △COD 相似时有两种情况，即 ∠FEC=90∘ 或 ∠EFC=90∘，
若 ∠FEC=90∘，则 PE⊥CE，
∴ 对称轴与 x 轴垂直，
∴ 此时抛物线的顶点即为满足条件的 P 点，此时 P 点坐标为 −1,4；
若 ∠EFC=90∘，则 PE⊥CD，
如图，过 P 作 PG⊥x 轴于点 G，
则 ∠GPE+∠PEG=∠DCO+∠PEG，
∴∠GPE=∠OCD，且 ∠PGE=∠COD=90∘，
∴△PGE∽△COD，
∴PGOC=GEOD，
∵E−1,0，Gt,0，且 P 点横坐标为 t，
∴GE=−1−t，PG=−t2−2t+3，
∴−t2−2t+33=−1−t1，解得 t=−2 或 t=3，
∵P 点在第二象限，
∴t<0，即 t=−2，
此时 P 点坐标为 −2,3，
综上可知满足条件的 P 点坐标为 −1,4 或 −2,3；
②设直线 CD 解析式为 y=kx+m，
把 C，D 两点坐标代入可得 −3k+m=0,m=1.，解得 k=13,m=1.
∴ 直线 CD 解析式为 y=13x+1，
如图 2，过 P 作 PN⊥x 轴，交 x 轴于点 N，交直线 CD 于点 M，
∵P 点横坐标为 t，
∴PN=−t2−2t+3，MN=13t+1，
∵P 点在第二象限，
∴P 点在 M 点上方，
∴PM=PN−MN=−t2−2t+3−13t+1=−t2−73t+2=−t+762+12136，
∴ 当 t=−76 时，PM 有最大值，最大值为 12136，
∵S△PCD=S△PCM+S△PDM=12PM⋅CN+12PM⋅NO=12PM⋅OC=32PM，
∴ 当 PM 有最大值时，△PCD 的面积有最大值，
∴S△PCDmax=32×12136=12124，
综上可知存在点 P 使 △PCD 的面积最大，△PCD 的面积有最大值为 12124．
26. （1） 在 Rt△ABC 中，BC=3，AC=4，
∴AB=5．
∵12BC⋅AC=12AB⋅CD，
∴CD=2.4．
∴r=2.4．
（2） 当点 A 在 ⊙C 上时，r=4．
∴ 当 2.4