2021年北京平谷区门楼庄中学九年级上期末数学试卷

这是一份2021年北京平谷区门楼庄中学九年级上期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共8小题；共40分）
1. 已知 ⊙O 的半径为 5 cm，若点 A 到圆心 O 的距离为 3 cm，则点 A
A. 在 ⊙O 内B. 在 ⊙O 上
C. 在 ⊙O 外D. 与 ⊙O 的位置关系无法确定

2. 四边形的外角和为
A. 180∘B. 360∘C. 540∘D. 720∘

3. 若函数 y=−x2+bx+c 的图象最高点是 1,−4，则 b，c 的值分别是
A. −2，−5B. 2，5C. −2，5D. 2，−5

4. 如图，∠ACB=90∘，CD 是 AB 边上的高，若 AD=24，BD=6，则 CD 的长是
A. 8B. 10C. 12D. 14

5. 关于反比例函数 y=2x，下列说法不正确的是
A. 函数图象分别位于第一、第三象限
B. 当 x>0 时，y 随 x 的增大而减小
C. 若点 Ax1,y1，Bx2,y2 都在函数图象上，且 x1y2
D. 函数图象经过点 1,2

6. 如图，⊙O 中，CD⊥AB 于点 E，若 ∠B=60∘，则 ∠A=
A. 30∘B. 45∘C. 60∘D. 90∘

7. 在做抛硬币试验时，甲、乙两个小组画出折线统计图后发现频率的稳定值分别是 50.00% 和 50.02%，则下列说法错误是
A. 乙同学的试验结果是错误的
B. 这两种试验结果都是正确的
C. 增加试验次数可以减小稳定值的差异
D. 同一个试验的稳定值不是唯一的

8. 某广场有一喷水池，水从地面喷出，如图，以水平地面为 x 轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线 y=−x2+4x（单位：米）的一部分，则水喷出的最大高度是
A. 4 米B. 3 米C. 2 米D. 1 米

二、填空题（共8小题；共40分）
9. 如图，分别以正三角形的 3 个顶点为圆心，边长为半径画弧，三段弧围成的图形称为莱洛三角形．若正三角形边长为 6 cm，则该莱洛三角形的周长为 cm．

10. 将抛物线 y=2x2 向左平移 1 个单位，再向下平移 2 个单位，所得图象的表达式为 ．

11. 如图，在 △ABC 中，点 D，E 分别在 AB，AC 上，连接 DE．
（1）若 ADDB=AEEC，则 DE BC（填“∥”或“=”）；
（2）若 ACAB= ，则 DE∥BC．

12. 请写出一个二次函数表达式，使其图象的对称轴为 y 轴： ．

13. 在直角坐标平面内有一点 A12,5，点 A 与原点 O 的连线与 x 轴的正半轴的夹角为 θ，那么 csθ= ．

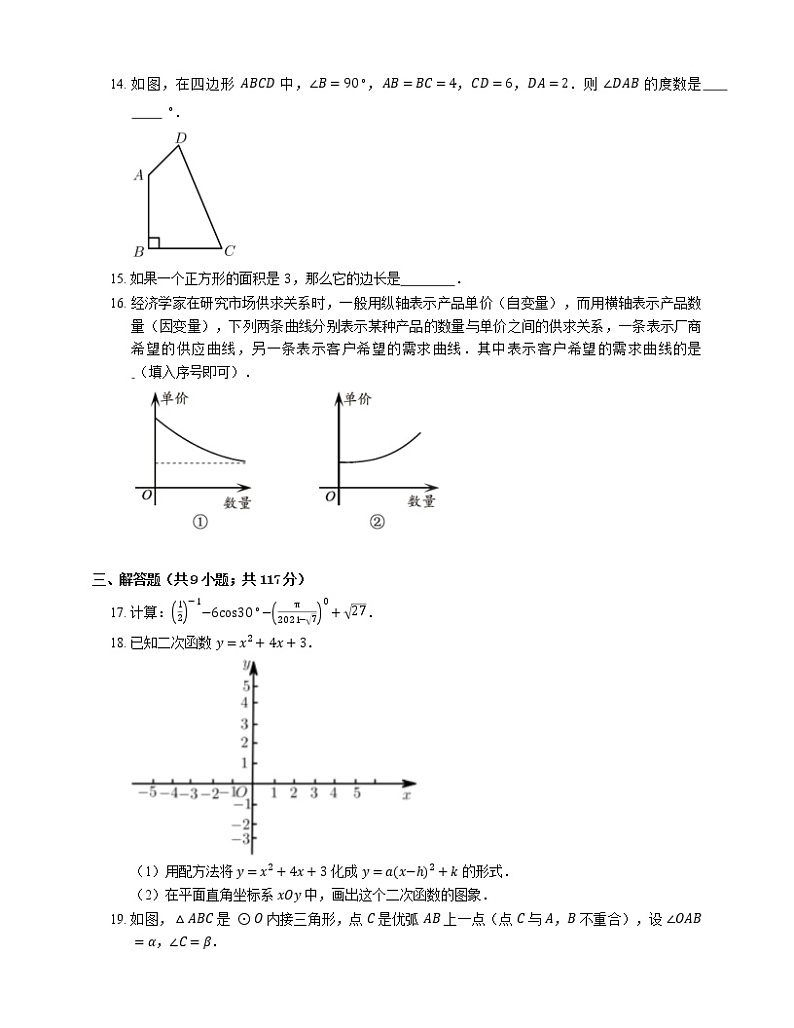
14. 如图，在四边形 ABCD 中，∠B=90∘，AB=BC=4，CD=6，DA=2．则 ∠DAB 的度数是 ∘．

15. 如果一个正方形的面积是 3，那么它的边长是 ．

16. 经济学家在研究市场供求关系时，一般用纵轴表示产品单价（自变量），而用横轴表示产品数量（因变量），下列两条曲线分别表示某种产品的数量与单价之间的供求关系，一条表示厂商希望的供应曲线，另一条表示客户希望的需求曲线．其中表示客户希望的需求曲线的是 （填入序号即可）．

三、解答题（共9小题；共117分）
17. 计算：12−1−6cs30∘−π2021−70+27．

18. 已知二次函数 y=x2+4x+3．
（1）用配方法将 y=x2+4x+3 化成 y=ax−h2+k 的形式．
（2）在平面直角坐标系 xOy 中，画出这个二次函数的图象．

19. 如图，△ABC 是 ⊙O 内接三角形，点 C 是优弧 AB 上一点（点 C 与 A，B 不重合），设 ∠OAB=α，∠C=β．
（1）当 α=35∘ 时，求 β 的度数；
（2）猜想 α 与 β 之间的关系，并给予证明．

20. 如图，经过原点的直线 y1 与双曲线 y2=kx（k 为常数，k≠0）交于 A，B 两点，其中点 A 的坐标为 1,2．
（1）求 k 的值；
（2）当 y1>y2 时，请你直接写出 x 的取值范围．

21. 某校为检测师生体温，在校门安装了某型号的测温门．如图为该“测温门”截面示意图．身髙 1.6 米的小聪做了如下实验：当他在地面 M 处时“测温门”开始显示额头温度，此时在额头 B 处测得 A 的仰角为 30∘；当他在地面 N 处时，“测温门”停止显示额头温度，此时在额头 C 处测得 A 的仰角为 53∘．如果测得小聪的有效测温区间 MN 的长度是 0.98 米，求测温门顶部 A 处距地面的高度约为多少米?（注：额头到地面的距离以身高计，sin53∘≈0.8，cs53∘≈0.6，ct53∘≈0.75，3≈1.73．）

22. 如图，在 Rt△ABC 中，∠ACB=90∘，以 AC 为直径作 ⊙O 交 AB 于点 D，连接 CD．
（1）求证：∠A=∠BCD．
（2）若 M 为线段 BC 上一点，试问当点 M 在什么位置时，直线 DM 与 ⊙O 相切?并说明理由．

23. 已知二次函数 y=ax2+bx+ca≠0 的图象过点 1,−2 和 −1,0 和 0,−32．
（1）求此二次函数的解析式；
（2）按照列表、描点、连线的步骤，在如图所示的平面直角坐标系内画出该函数的图象（要求至少 5 点）．

24. （1）如图①，若 BC=6，AC=4，∠C=60∘，求 △ABC 的面积 S△ABC；
（2）如图②，若 BC=a，AC=b，∠C=α，求 △ABC 的面积 S△ABC；
（3）如图③，四边形 ABCD，若 AC=m，BD=n，对角线 AC，BD 交于 O 点，它们所成的锐角为 β．求四边形 ABCD 的面积 S四边形ABCD．

25. 在平面直角坐标系 xOy 中，横、纵坐标都是整数的点叫做整点．给出如下定义：对于任意两个整点 Mx1,y1，Nx2,y2，M 与 N 的“直角距离”记为 dMN，dMN=∣x1−x2∣+∣y1−y2∣．例如，点 M1,5 与 N7,2 的“直角距离”dMN=∣1−7∣+∣5−2∣=9．
（1）已知点 A4,−1．
①点 A 与点 B1,3 的“直角距离”dAB= ；
②若点 A 与整点 C−2,m 的“直角距离”dAC=8，则 m 的值为 ；
（2）小明有一项设计某社区规划图的实践作业，这个社区的道路都是正南正北，正东正西方向，并且平行的相邻两条路之间的距离都是相等的，可近似看作正方形的网格．小明建立平面直角坐标系画出了此社区的示意图（如图所示）．
为了做好社区消防，需要在某个整点处建一个消防站 P，要求是：消防站与各个火警高危点的“直角距离”之和最小．目前该社区内有两个火警高危点，分别是 D−2,−1 和 E2,2．
①若对于火警高危点 D 和 E，消防站 P 不仅要满足上述条件，还需要消防站 P 到 D，E 两个点的“直角距离”之差的绝对值最小，则满足条件的消防站 P 的坐标可以是 （写出一个即可），所有满足条件的消防站 P 的位置共有 个；
②在设计过程中，如果社区还有一个火警高危点 F4,−2，那么满足与这三个火警高危点的“直角距离”之和最小的消防站 P 的坐标为 ．
答案
第一部分
1. A【解析】∵OA=3 cm0，
A、函数图象分别位于第一、三象限，正确；
B、当 k>0，双曲线的两支分别位于第一、第三象限，当 x>0 时，y 随 x 的增大而减小，正确；
C、若点 Ax1,y1，Bx2,y2 都在函数图象上，且 x1