2021年北京石景山区同文中学九年级上期末数学试卷

这是一份2021年北京石景山区同文中学九年级上期末数学试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题；共50分）
1. 在 Rt△ABC 中，∠C=90∘，AC=1，BC=3，则 ∠A 的正切值为
A. 3B. 13C. 1010D. 31010

2. 抛物线 y=2x+12−3 的顶点坐标为
A. 1,3B. 1,−3C. −1,3D. −1,−3

3. 如果两个相似三角形对应边之比是 1:3，那么它们的对应中线之比是
A. 1:3B. 1:4C. 1:6D. 1:9

4. 以下列长度（同一单位）为长的四条线段中，不成比例的是
A. 2，5，10，25B. 4，7，4，7
C. 2，12，12，4D. 2，5，25，52

5. 如图，△ABC 中，∠C=90∘，BC=5，⊙O 与 △ABC 的三边相切于点 D，E，F，若 ⊙O 的半径为 2，则 △ABC 的周长为
A. 14B. 20C. 24D. 30

6. 已知函数 y=kx，当 x=1 时，y=−3，那么这个函数的解析式是
A. y=3xB. y=−3xC. y=13xD. y=−13x

7. 如图，一个三角尺 ABC 的斜边 AB 与量角器的直径恰好重合，点 D 对应的刻度是 46∘，则 ∠ACD 的度数为
A. 46∘B. 23∘C. 44∘D. 67∘

8. 选一选。
在同一平面直角坐标系中，若抛物线y=x2+(2m−1)x+2m−4与y=x2−(3m+n)x+n关于y轴对称，则符合条件的m，n的值为（ ）
A. m=57，n=−187B. m=5，n=−6C. m=−1，n=6D. m=1，n=−2

9. 已知 AB 为 ⊙O 的直径，C 为 ⊙O 上一点，过点 C 作 CD⊥AB，垂足为点 D，延长 CD 至点 E，使 DE=CD，那么点 E 的位置是
A. 在 ⊙O 内B. 在 ⊙O 上C. 在 ⊙O 外D. 不能确定

10. 如图①，在长方形 ABCD 中，动点 P 从点 B 出发，沿 BC，CD，DA 运动至点 A 停止，设点 P 运动的路程为 x，△ABP 的面积为 y，如果 y 与 x 之间的图象如图②所示，则长方形 ABCD 的面积是
A. 10B. 16C. 20D. 36

二、填空题（共6小题；共30分）
11. 已知函数 y=−2x2+x−4，当 x< 时，y 随 x 的增大而增大；当 x> 时，y 随 x 的增大而减小；当 x= 时，y 最大值为 ．

12. 一个扇形的面积是它所在圆面积的 35，则这个扇形的圆心角是 ．

13. 抛物线 y=12x2 向上平移 2 个单位长度后得到的新抛物线的解析式为 ．

14. 若反比例函数 y=k−2x 的图象经过第一、三象限，则 k 的取值范围是 ．

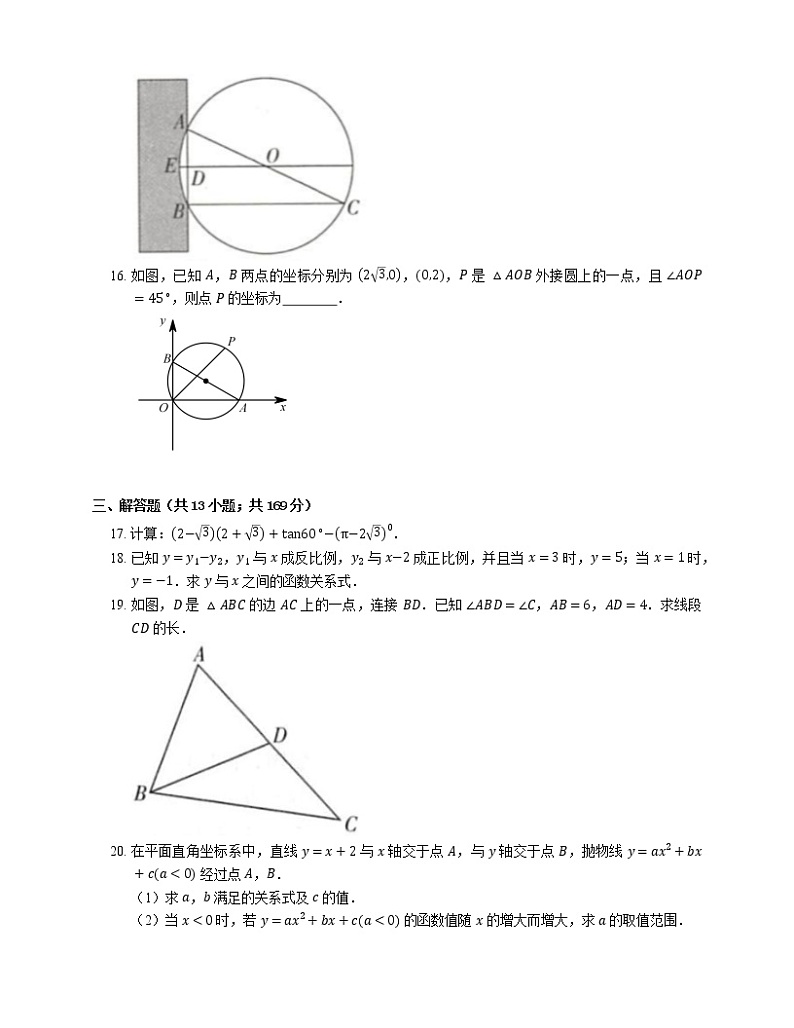
15. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何?”意思是：今有一圆柱形木材，埋在墙壁中（如图所示），不知其大小．用锯去锯这木材，锯口深 ED=1 寸，锯道长 AB=1 尺（1 尺 =10 寸）．则这根圆柱形木材的底面直径是 寸．

16. 如图，已知 A，B 两点的坐标分别为 23,0，0,2，P 是 △AOB 外接圆上的一点，且 ∠AOP=45∘，则点 P 的坐标为 ．

三、解答题（共13小题；共169分）
17. 计算：2−32+3+tan60∘−π−230．

18. 已知 y=y1−y2，y1 与 x 成反比例，y2 与 x−2 成正比例，并且当 x=3 时，y=5；当 x=1 时，y=−1．求 y 与 x 之间的函数关系式．

19. 如图，D 是 △ABC 的边 AC 上的一点，连接 BD．已知 ∠ABD=∠C，AB=6，AD=4．求线段 CD 的长．

20. 在平面直角坐标系中，直线 y=x+2 与 x 轴交于点 A，与 y 轴交于点 B，抛物线 y=ax2+bx+ca2
15. 26
【解析】由题意可知 OE⊥AB，
因为 OE 为 ⊙O 的半径，
所以 AD=BD=12AB=12 尺 =5 寸，
设半径 OA=r 寸，则 OE=r 寸，
因为 ED=1 寸，
所以 OD=r−1 寸，则在 Rt△OAD 中，根据勾股定理可得 r−12+52=r2，解得 r=13，
所以这根圆柱形木材的底面直径为 13×2=26 寸．
16. 3+1,3+1 或 3−1,1−3
【解析】∵OB=2，OA=23，
∴AB=OA2+OB2=4，
∵∠AOP=45∘，
∴P 点横纵坐标相等，可设为 a，即 Pa,a，
∵∠AOB=90∘，
∴AB 是直径，
∴Rt△AOB 外接圆的圆心为 AB 中点，坐标 C3,1，
可得 P 点在圆上，P 点到圆心的距离为圆的半径 2，过点 C 作 CF∥OA，过点 P 作 PE⊥OA 于 E 交 CF 于 F，
∴∠CFP=90∘，
∴PF=a−1，CF=a−3，PC=2，
∴ 在 Rt△PCF 中，利用勾股定理得：a−32+a−12=22，
解得 a=0 或 a=1+3，
舍去不合适的根，可得：a=1+3，
则 P 点坐标为 3+1,3+1．
∵P 与 Pʹ 关于圆心 3,1 对称，
∴Pʹ3−1,1−3．
第三部分
17. 原式=22−32+3−1=4−3+3−1=3.
18. 设 y1=k1x，y2=k2x−2，
所以 y=k1x−k2x−2，
由 k13−k2=5,k1+k2=−1,
解得 k1=3,k2=−4.
所以 y=3x+4x−2．
19. 在 △ABD 与 △ACB 中，∠ABD=∠C，∠A=∠A，
∴△ABD∽△ACB．
∴ABAC=ADAB．
又 AB=6，AD=4，
∴6AC=46．
解得 AC=9．
∴CD=AC−AD=9−4=5．
20. （1） y=x+2，令 x=0，则 y=2；令 y=0，则 x=−2，
故点 A，B 的坐标分别为 −2,0，0,2，则 c=2，
则函数表达式为：y=ax2+bx+2，
将点 A 坐标代入上式并整理得：b=2a+1．
（2） 当 x