2021年北京朝阳区芳草地国际学校富力分校(初中部)九年级上期末数学试卷

这是一份2021年北京朝阳区芳草地国际学校富力分校(初中部)九年级上期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共8小题；共40分）
1. 抛物线 y=−4x−m2+n（m，n 是常数）的顶点坐标是
A. −m,nB. m,nC. m,−nD. −m,−n

2. 如图，一个长方形纸片，剪去部分后得到一个三角形，则图中 ∠1+∠2 的度数是
A. 30∘B. 60∘C. 90∘D. 120∘

3. 如图，点 A，B 分别在双曲线 y=1x 和 y=3x 上，点 C，D 在 x 轴上，且四边形 ABCD 为矩形，则矩形 ABCD 的面积为
A. 1B. 2C. 3D. 4

4. 已知圆锥的母线为 5 cm，底面直径为 4 cm，这个圆锥的侧面积为
A. 20π cm2B. 20 cm2C. 10π cm2D. 10 cm2

5. 如图，在半径为 5 cm 的 ⊙O 中，圆心 O 到弦 AB 的距离为 3 cm，则弦 AB 的长是
A. 4 cmB. 6 cmC. 8 cmD. 10 cm

6. 如图，点 C 是线段 AB 的黄金分割点 AC>BC，则下列结论中正确的是
A. AB2=AC2+BC2B. BC2=AC⋅BA
C. AC2=AB⋅BCD. AC=2BC

7. 若点 A1,y1，B2,y2 在抛物线 y=ax+12+2ay1>y2B. 2>y2>y1C. y1>y2>2D. y2>y1>2

8. “割圆术”是我国古代的一位伟大的数学家刘徽首创的，该割圆术，就是通过不断倍增圆内接正多边形的边数来求出圆周率 π 的一种方法．某同学在学习“割圆术”的过程中，画了一个如图所示的圆的内接正十二边形，若该圆的半径为 1，则这个圆的内接正十二边形的面积为
A. 1B. 3C. 3.1D. 3.14

二、填空题（共8小题；共40分）
9. 若 ∠A 是锐角，且 tanA=3，则 csA= ．

10. 如图，在 ⊙0 中，已知 ∠AOB=120∘，则 ∠ACB= ．

11. 一个二次函数，当 x=4 时有最小值为 0，图象形状与 y=3x2 相同，则该二次函数的解析式为 ．

12. 如图，为了测量某风景区内一座古塔 AB 的高度，小明分别在塔的对面一楼层 CD 的楼底 C，楼顶 D 处，测得塔顶 A 的仰角为 45∘ 和 30∘，已知楼高 CD 为 10 m，则塔 AB 的高度为 m．

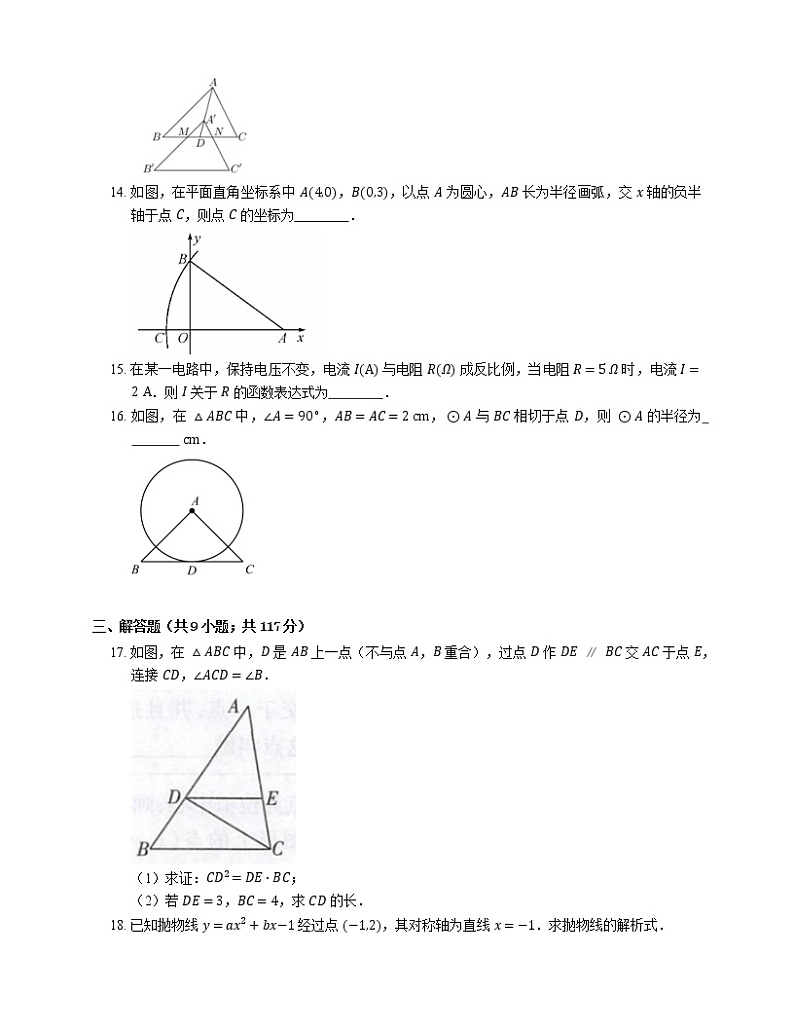
13. 如图，将 △ABC 沿 BC 边上的中线 AD 平移到 △AʹBʹCʹ 的位置，如果点 Aʹ 恰好是 △ABC 的重心，AʹBʹ 、 AʹCʹ 分别于 BC 交于点 M，N，那么 △AʹMN 的面积与 △ABC 的面积之比是 ．

14. 如图，在平面直角坐标系中 A4,0，B0,3，以点 A 为圆心，AB 长为半径画弧，交 x 轴的负半轴于点 C，则点 C 的坐标为 ．

15. 在某一电路中，保持电压不变，电流 IA 与电阻 RΩ 成反比例，当电阻 R=5 Ω 时，电流 I=2 A．则 I 关于 R 的函数表达式为 ．

16. 如图，在 △ABC 中，∠A=90∘，AB=AC=2 cm，⊙A 与 BC 相切于点 D，则 ⊙A 的半径为 cm．

三、解答题（共9小题；共117分）
17. 如图，在 △ABC 中，D 是 AB 上一点（不与点 A，B 重合），过点 D 作 DE∥BC 交 AC 于点 E，连接 CD，∠ACD=∠B．
（1）求证：CD2=DE⋅BC；
（2）若 DE=3，BC=4，求 CD 的长．

18. 已知抛物线 y=ax2+bx−1 经过点 −1,2，其对称轴为直线 x=−1．求抛物线的解析式．

19. 如图，点 A，B，C 表示三个村庄，现要建一座水泵站，向三个村庄分别送水，为使三条输水管道长度相同，水泵站应建在何处?请画出图形，并说明理由．

20. 反比例函数 y=kx 过点 3,−4，
（1）求反比例函数的解析式．
（2）当 −3≤x0 时，y= ．
（3）在给定的坐标系中，已经画出了当 x≤0 时的函数图象，请根据（2）中的解析式，通过描点，连线，画出当 x>0 时的函数图象．
（4）在给定的坐标系中画直线 y=12，观察图象可知方程 xx−2=12 的实数根有 个．
（5）深入探究：若关于 x 的方程 2xx−2=m 有三个不相等的实数根，且这三个实数根的和为负数，则 m 的取值范围是 ．

23. 如图，点 M，N 分别在正方形 ABCD 的边 BC，CD 上，且 ∠MAN=45∘，把 △ADN 绕点 A 顺时针旋转 90∘ 得到 △ABE．
（1）求证：△AEM≌△ANM；
（2）若 BM=3，DN=2，求正方形 ABCD 边长．

24. 平面直角坐标系 xOy 中，抛物线 y=x2−2mx+m2−3 与 y 轴交于点 A，过 A 作 AB∥x 轴与直线 x=4 交于点 B．
（1）抛物线的对称轴为 x= （用含 m 的代数式表示）；
（2）当抛物线经过点 A，B 时，求抛物线的表达式．

25. 如图，在 Rt△ABC 中，∠ACB=90∘，AC=BC=3，点 D 在边 AC 上，且 AD=2CD，DE⊥AB，垂足为点 E，连接 CE．求：
（1）线段 BE 的长；
（2）∠ECB 的余切值．
答案
第一部分
1. B
2. C
3. B【解析】设 OD=a．
把 x=a 代入 y=1x 得 y=1a，即 AD=1a；
把 y=1a 代入 y=3x 得 x=3a，即 OC=3a．
∴CD=OC−OD=2a．
∴ 矩形 ABCD 的面积 =CD⋅AD=2a×1a=2．
故选：B．
4. C
5. C
【解析】连接 OA，
∵OD⊥AB，如图，
∴AD=BD，OD=3 cm，
在 Rt△AOD 中，OA=5 cm，OD=3 cm，
∴AD=OA2−OD2=4 cm，
∴AB=2AD=8 cm．
6. C
7. A
8. B【解析】由题意，在半径为 1 的圆中内接正十二边形，
则将该正十二边形划分为十二个三角形，
则面积
S=12×12×a⋅b⋅sinca=b=r=1,∠c=360∘12=30∘=12×12×1×1×sin30∘=3.
第二部分
9. 12
【解析】∵tanA=3，
∴∠A=60∘，
∴csA=12．
10. 60∘
11. y=3x−42
12. 15+53
13. 19
【解析】∵△ABC 沿 BC 边上的中线 AD 平移到 △AʹBʹCʹ 的位置，
∴AʹM∥AB，AʹN∥AC，
∴∠AʹMN=∠B，∠AʹNM=∠C，
∴△AʹMN∽△ABC，
∵AD 和 AʹD 分别是 △AʹMN 和 △ABC 对应边上的中线，点 Aʹ 恰好是 △ABC 的重心，
∴AʹDAD=AʹMAB=13，
∴△AʹMN 的面积与 △ABC 的面积之比是：19．
14. −1,0
15. I=10R
16. 2
【解析】连接 AD，
∵⊙A 与 BC 相切于点 D，
∴AD⊥BC．
又 ∵∠A=90∘，AB=AC，
∴∠B=∠C=45∘．
在 Rt△ADB 中，AD=ABsin45∘=2，⊙A 的半径为 2 cm．
第三部分
17. （1） ∵DE∥BC，
∴∠EDC=∠DCB．
又 ∠ACD=∠B，
∴△DEC∽△CDB．
∴DECD=CDBC．
∴CD2=DE⋅BC．
（2） ∵CD2=DE⋅BC，DE=3，BC=4，
∴CD2=3×4=12．
∴CD=23（负值舍去）．
18. 由题意，得 a−b−1=2,−b2a=−1. 解得 a=−3,b=−6.
∴ 抛物线的解析式为 y=−3x2−6x−1．
19. 如图，分别作线段 AB，BC 的垂直平分线，
它们的交点 О 即是水泵站应建的位置．
理由：线段的垂直平分线上的点到线段的两个端点的距离相等．
20. （1） 把点 3,−4 代入 y=kx 得 −4=k3，
解得 k=−12，
∴y=−12x．
（2） 当 x=−3 时，y=4，
当 x=−1 时，y=12，
∴ 当 −3≤x