数学六年级下册5 数学广角 （鸽巢问题）优质ppt课件

这是一份数学六年级下册5 数学广角 （鸽巢问题）优质ppt课件，文件包含52《鸽巢问题二》课件25页pptx、52《鸽巢问题二》教案教学设计docx、52《鸽巢问题二》同步练习doc等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。
进一步熟知“鸽巢原理”的含义，会用“鸽巢原理”熟练解决简单的实际问题
应用“鸽巢原理”解决实际问题。引导学会把具体问题转化成“鸽巢问题”
理解“鸽巢原理”，找出”鸽巢问题“解决的窍门进行反复推理
一天晚上，毛毛房间的电灯突然坏了，伸手不见五指，这时他又要出去，于是他就摸床底下的袜子，他有蓝、白、灰色的袜子各一双，由于他平时做事随便，袜子乱丢，在黑暗中不知道哪些袜子颜色是相同的。毛毛想拿最少数目的袜子出去，在外面借街灯配成相同颜色的一双。你们知道最少拿几只袜子出去吗？
盒子里有同样大小的红球和蓝球各4个，要想摸出的球一定有2个同色的，最少要摸出几个球？
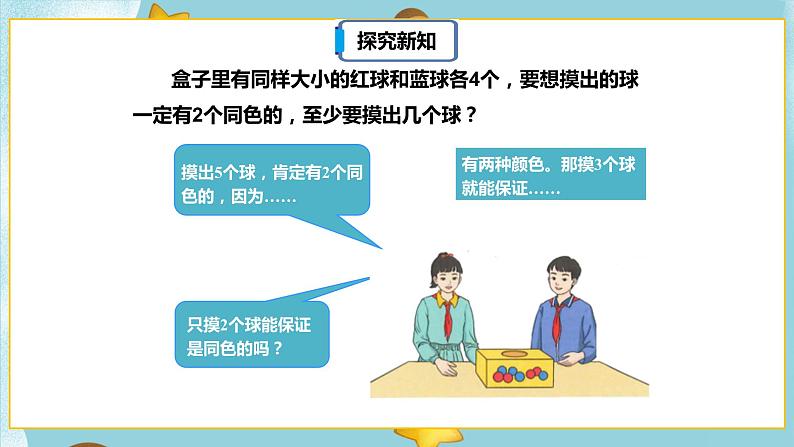
摸出5个球，肯定有2个同色的，因为……
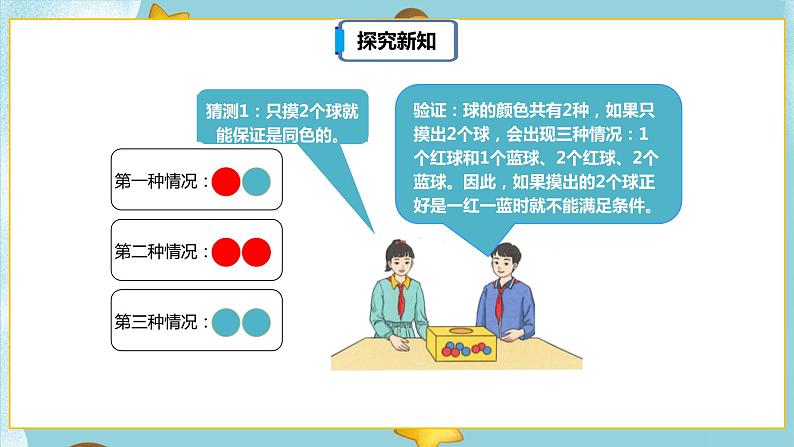
盒子里有同样大小的红球和蓝球各4个，要想摸出的球一定有2个同色的，至少要摸出几个球？
有两种颜色。那摸3个球就能保证……
生活中像这样的例子很多，我们能不能把这道题与前面所讲的“鸽巢问题”联系起来进行思考呢？
a.“摸球问题”与“鸽巢问题”有怎样的联系？b.应该把什么看成“鸽巢”？有几个“鸽巢”？ 要分放的东西是什么？c.得出什么结论？
因为一共有红、蓝两种颜色的球，可以把两种“颜色”看成两个“鸽巢”，“同色”就意味着“同一个鸽巢”。这样，把“摸球问题”转化“鸽巢问题”，即“只要分的物体个数比鸽巢多，就能保证有一个鸽巢至少有两个球”。
1.六年级有47名学生参加一次数学竞赛，成绩都是整数，满分是100分。已知3名学生的成绩在60分以下，其余学生的成绩均在75~95分之间。问：至少有几名学生的成绩相同？
47-3=44（名） 95 - 75 + 1=2144÷21=2……2 2+1=3（名）答：这47名学生中至少有3名学生的成绩是相同的。
2. 向东小学六年级共有367名学生，其中六（2）班有49名学生。
他们说得对吗？为什么？
367÷365＝1······2
49÷12＝4······1
3. 把红、黄、蓝、白四种颜色的球各10个放到一个袋子里。至少取多少个球，可以保证取到两个颜色相同的球？
我们从最不利的原则去考虑：
假设我们每种颜色的都拿一个，需要拿4个，但是没有同色的，要想有同色的需要再拿1个球，不论是哪一种颜色的，都一定有2个同色的。
4. 希望小学篮球兴趣小组的同学中，最大的12岁，最小的6岁，最少从中挑选几名学生，就一定能找到两个学生年龄相同。
5. 从一副扑克牌（52张，没有大小王）中要抽出几张牌来，才能保证有一张是红桃？54张呢？
2＋13×3＋1＝42
6.给一个正方体木块的6个面分别涂上蓝、黄两种颜色。不论怎么涂至少有3个面涂的颜色相同。为什么？
用抽屉原理（鸽巢原理）解题的一般步骤：分析题意，把实际问题转化成抽屉问题，即弄清抽屉和分放的物体，根据抽屉原理推理并解决问题。
1.随意找13位老师，他们中至少有2个人的属相相同。为什么？