初中数学浙教版七年级下册3.3 多项式的乘法习题ppt课件

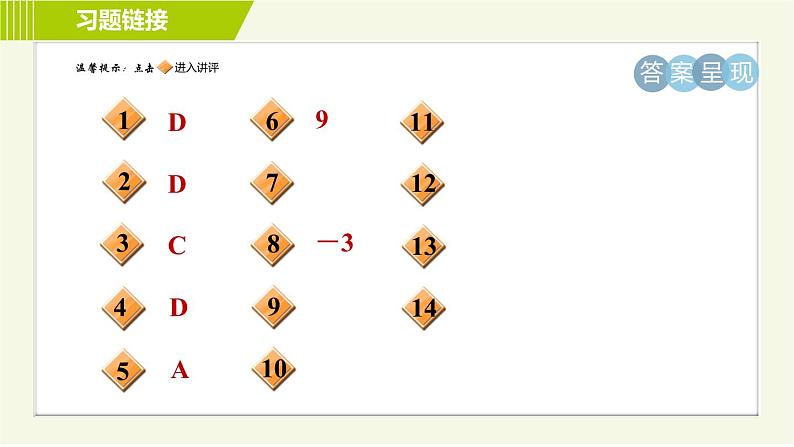
这是一份初中数学浙教版七年级下册3.3 多项式的乘法习题ppt课件，共30页。PPT课件主要包含了答案呈现，习题链接，1求ab的值等内容，欢迎下载使用。
计算(2x－3)(3x＋4)的结果，与下列式子相同的是(　　)A．－7x＋4 B．－7x－12C．6x2－12 D．6x2－x－12
如图，可以用两条互相垂直的线段把大长方形的面积分成四个小长方形的面积，根据这种面积关系得到的等式是(　　)A．(x＋p)(x＋q)＝x2＋pqB．(x＋p)2＝x2＋2px＋p2C．(x＋p)(x＋q)＝x2＋(p＋q)x＋pqD．x2－q2＝(x＋q)(x－q)
当x＝1时，ax＋b＋1的值为－2，则(a＋b－1)(1－a－b)的值为(　　)A．－16 B．－8 C．8 D．16
【温州期末】若(x＋p)(x＋q)＝x2＋3x＋2，则(p＋q)2＝________.
【杭州月考】如果(2x＋1)(m－x)的展开式只有两项，则常数m的值为________．
【绍兴期末】已知m＋n＝2，mn＝－2，则(1－m)(1－n)的值为________．
计算：(1)(x＋1)(x－1)； (2)(2a－b)(a＋b)；
解：原式＝x2－x＋x－1＝x2－1.
原式＝2a2＋2ab－ab－b2＝2a2＋ab－b2.
(3)(x＋3y)(x－2y)；  (4)(5x＋2y)(3x－2y)．
解：原式＝x2－2xy＋3xy－6y2＝x2＋xy－6y2.
原式＝15x2－10xy＋6xy－4y2＝15x2－4xy－4y2.
先化简，再求值：(1)【中考·宁波】(x－2)(x＋2)－x(x－1)，其中x＝3；　
解：(x－2)(x＋2)－x(x－1)＝x2＋2x－2x－4－x2＋x＝x－4.当x＝3时，x－4＝3－4＝－1.
若x2＋3x－5＝a(x＋1)2＋b(x＋1)＋c，则a＝________，b＝________，c＝________.
甲，乙两人共同计算一个整式：(x＋a)(2x＋b)，由于甲抄错了a的符号，得到的结果是2x2－7x＋3，乙漏抄了第二个多项式中x的系数，得到的结果是x2＋2x－3.
解：甲抄错了a的符号，计算结果为(x－a)(2x＋b)＝2x2＋(－2a＋b)x－ab＝2x2－7x＋3，∴－2a＋b＝－7，ab＝－3.乙漏抄了第二个多项式中x的系数，计算结果为：(x＋a)(x＋b)＝x2＋(a＋b)x＋ab＝x2＋2x－3.∴a＋b＝2，ab＝－3.
(2)请计算这道题的正确结果．
解：正确的计算结果：(x＋3)(2x－1)＝2x2＋5x－3.
在通常的月历表上可以看到一些数满足的规律，表1是某月的月历表．
(1)在表1中，我们选择用如表2那样的2×2的长方形方框任意框出2×2个数，将它们交叉相乘再相减(大数减小数)，如：2×8－1×9＝7，14×20－13×21＝7.你发现了什么规律？想一想，能否用整式的运算加以说明．
解：发现结果均为7.能．理由：设最小数为n，则另外三个数分别为n＋1，n＋7，n＋8.(n＋1)(n＋7)－n(n＋8)＝n2＋7n＋n＋7－n2－8n＝7.
(2)如果选择用如表3那样的3×3的长方形方框任意框出3×3个数，将长方形方框的四个角位置上的4个数交叉相乘再相减(大数减小数)，你又发现了什么规律？请说明理由．
解：发现结果均为28.理由：设左上角的数为m，则另外三个数分别为m＋2，m＋14，m＋16.(m＋2)(m＋14)－m(m＋16)＝m2＋14m＋2m＋28－m2－16m＝28.
在整式乘法的学习中，我们采用了构造几何图形的方法研究代数式的变形问题，借助直观、形象的几何图形，加深对整式乘法的认识和理解，感悟代数与几何的内在联系．如图①，现有边长分别为a，b的正方形Ⅰ号和Ⅱ号，以及长为a，宽为b的长方形Ⅲ号卡片足够多，我们可以选取适量的卡片拼接成几何图形．(卡片间不重叠、无缝隙)
根据已有的学习经验，解决下列问题：
(1)图②甲是由1张Ⅰ号卡片、1张Ⅱ号卡片、2张Ⅲ号卡片拼接成的正方形，那么这个几何图形表示的等式是_____________________；
(a＋b)2＝a2＋2ab＋b2
(2)小聪想用几何图形表示等式(a＋b)(2a＋b)＝2a2＋3ab＋b2，图②乙给出了他所拼接的几何图形的一部分，请你补全图形；