华师大版19.3 正方形习题ppt课件

这是一份华师大版19.3 正方形习题ppt课件，共33页。PPT课件主要包含了答案显示，新知笔记，基础巩固练，见习题，相等且互相垂直平分，答案2021，答案C，BC＝CD＋CF等内容，欢迎下载使用。

(1)相等　(2)直角　(3)相等且互相垂直平分
正方形既是中心对称图形，也是轴对称图形，它具有以下性质：(1)四条边都__________；(2)四个角都是__________；(3)对角线_____________________．
1．【中考•遂宁】下列说法正确的是(　　)A．有两条边和一个角对应相等的两个三角形全等B．正方形既是轴对称图形又是中心对称图形C．矩形的对角线互相垂直平分D．六边形的内角和是540°
2．正方形具有而菱形不一定具有的性质是(　　)A．对角线互相平分 B．对角线相等C．对角线互相垂直 D．每条对角线平分一组对角
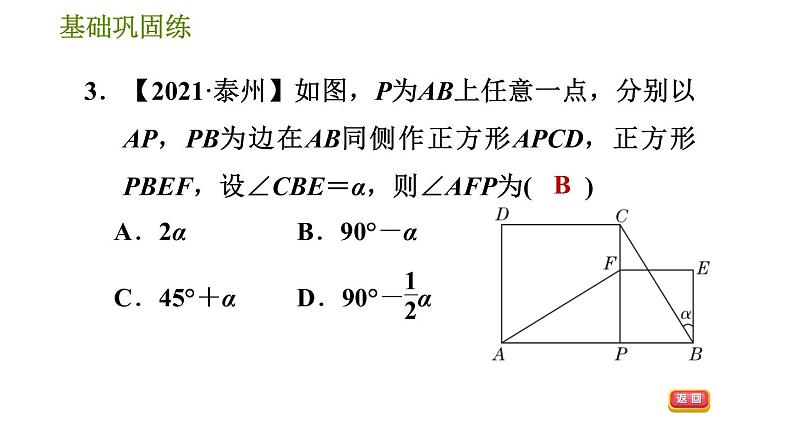
3．【2021·泰州】如图，P为AB上任意一点，分别以AP，PB为边在AB同侧作正方形APCD，正方形PBEF，设∠CBE＝α，则∠AFP为(　　)
4．如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置．若四边形AECF的面积为25，DE＝2，则AE的长为(　　)
5．【中考·鄂尔多斯】如图，在正方形ABCD的外侧，作等边三角形ABE，则∠BED为(　　)A．15° B．35° C．45° D．55°
6．【荣德原创】将2 022个边长为2的正方形按照如图所示的方式摆放，O1，O2，O3，O4，O5，…，O2 022分别是正方形对角线的交点，那么这2 021个正方形重叠部分(阴影部分)的面积之和为________．
7．【创新题】如图，在正方形ABCD中，BD为对角线，E，F分别是AD，CD上的点，且AE＝CF，连结BE，BF，EF.(1)求证：EM＝FM；
证明：∵四边形ABCD是正方形，∴AD＝CD，∠ADB＝∠CDB＝45°，又∵AE＝CF，∴DE＝DF，∴EM＝FM.
(2)若AB＝4，AF＝1，求四边形BEDF的面积．
8．【中考·仙桃】如图，正方形ABCD中，AB＝6，G是BC的中点，将△ABG沿AG折叠至△AFG处，延长GF交DC于点E，则DE的长是(　　)A．1 B．1.5 C．2 D．2.5
9．【中考·攀枝花】如图，在正方形ABCD中，E是BC边上的一点，BE＝4，EC＝8，将正方形边AB沿AE折叠到AF，延长EF交DC于G，连结AG，FC，现在有如下4个结论：①∠EAG＝45°；②FG＝FC；③FC∥AG；④S△GFC＝14.其中正确结论的个数是(　　)A．1 B．2 C．3 D．4
10.【创新题】【中考·河南】我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为(　　)
11．【中考·贵阳】如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF＝90°，连结CE，CF.(1)求证：△ABF≌△CBE；
证明：∵四边形ABCD是正方形，∴AB＝CB，∠ABC＝90°.∵△EBF是等腰直角三角形，∠EBF＝90°，∴BE＝BF.
(2)判断△CEF的形状，并说明理由．
解：△CEF是直角三角形．理由如下：∵△EBF是等腰直角三角形，∠EBF＝90°，∴∠BFE＝∠FEB＝45°.∴∠AFB＝180°－∠BFE＝135°.又∵△ABF≌△CBE，∴∠CEB＝∠AFB＝135°.∴∠CEF＝∠CEB－∠FEB＝135°－45°＝90°.∴△CEF是直角三角形．
12．【2021·南京期中】如图，在正方形ABCD中，点E，F，G分别在CD，AD，BC上，FG⊥BE，垂足为O.(1)求证：BE＝FG；
证明：作AM∥FG交BE于N，交BC于M.∵FG⊥BE，∴∠FOB＝90°.∵AM∥FG，∴∠ANB ＝∠FOB ＝90°.∴∠ABN＋∠BAM＝90°.∵四边形ABCD是正方形，
解：连结BF，EF，∵FG⊥BE，O是BE的中点，∴BF＝FE.∵四边形ABCD是正方形，∴AD＝AB＝DC＝BC＝8.∵EC＝3，∴DE＝5.设AF＝x，则DF＝8－x.
(2)若O是BE的中点，BC＝8，EC＝3，求AF的长．
13．某数学兴趣小组在数学课外活动中，研究三角形和正方形的性质时，做了如下探究：在△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上一动点(点D不与B，C重合)，以AD为边在AD右侧作正方形ADEF，连结CF.
(1)观察猜想如图①，当点D在线段BC上时，①BC与CF的位置关系为________，②BC，CD，CF之间的数量关系为_______________．(将结论直接写在横线上)
(2)数学思考如图②，当点D在线段CB的延长线上时，结论①②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
解：①成立．②不成立，正确结论为BC＝CD－CF.证明：∵四边形ADEF是正方形，∴AD＝AF，∠DAF＝90°.∵∠BAC＝90°，
∴∠DAB＝∠DAF－∠BAF＝∠BAC－∠BAF＝∠FAC.∵AD＝AF，AB＝AC，∴△DAB≌△FAC.∴BD＝CF，∠DBA＝∠FCA.∵∠BAC＝90°，AB＝AC，∴∠ABC＝∠ACB＝45°.∴∠DBA＝∠FCA＝135°.∴∠BCF＝∠FCA－∠ACB＝90°.∴CF⊥BC.∵BC＝CD－BD，BD＝CF，∴BC＝CD－CF.
【点拨】对于线段之间关系的结论猜想题，一般要考虑两种情况：一是位置关系，即平行或垂直；二是数量关系，即相等或倍数关系，若是三条线段，一般存在三者间的和差关系．这两种情况下的结论一般可以通过观察图形得到．如此题中，BC与CF的垂直关系易得，而BC，CD，CF之间的数量关系在不同图形中也容易辨识．