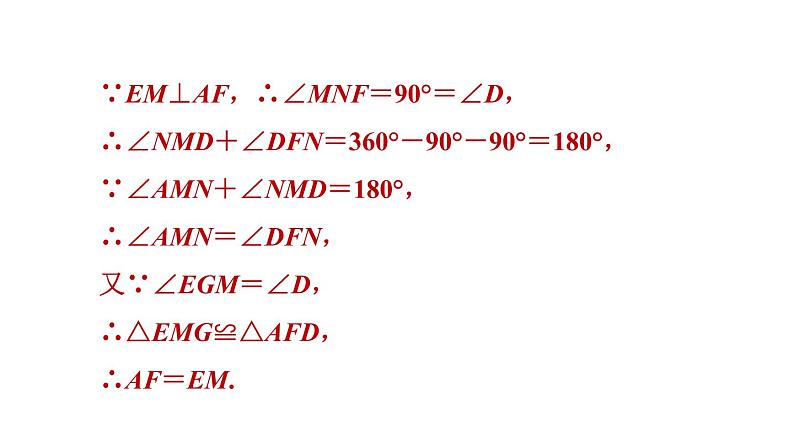
初中华师大版19.3 正方形习题课件ppt

这是一份初中华师大版19.3 正方形习题课件ppt，共32页。PPT课件主要包含了答案显示，见习题等内容，欢迎下载使用。

1．如图，在正方形ABCD中，对角线AC，BD相交于点O，E，F分别在OD，OC上，且DE＝CF，连结DF，AE，延长AE交DF于点M.求证：AM⊥DF.
证明：∵AC，BD是正方形ABCD的两条对角线，∴AC⊥BD，OA＝OD＝OC＝OB.∵DE＝CF，∴OE＝OF.在△AOE与△DOF中，
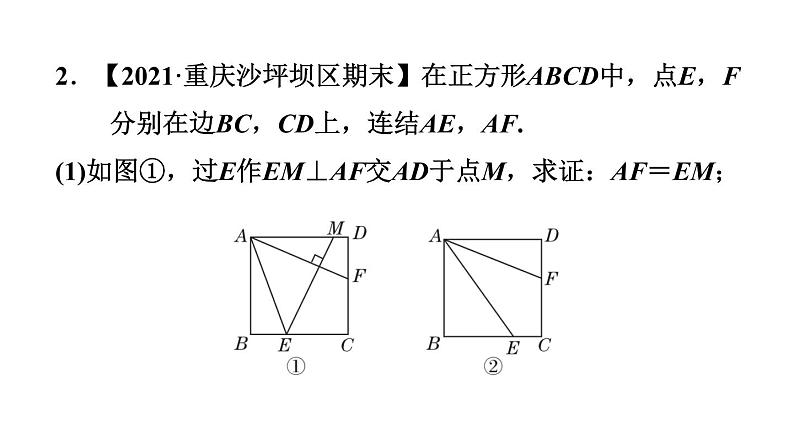
2．【2021·重庆沙坪坝区期末】在正方形ABCD中，点E，F分别在边BC，CD上，连结AE，AF.(1)如图①，过E作EM⊥AF交AD于点M，求证：AF＝EM；
∵EM⊥AF，∴∠MNF＝90°＝∠D，∴∠NMD＋∠DFN＝360°－90°－90°＝180°，∵∠AMN＋∠NMD＝180°，∴∠AMN＝∠DFN，又∵∠EGM＝∠D，∴△EMG≌△AFD，∴AF＝EM.
(2)如图②，若AE平分∠BAF，求证：AF＝BE＋DF.
∴∠AEH＝∠DAE＝∠DAF＋∠FAE，∵AE平分∠BAF，∴∠BAE＝∠FAE，∴∠HAE＝∠BAH＋∠BAE＝∠DAF＋∠FAE＝∠AEH，∴AH＝EH＝BE＋HB＝BE＋DF.∴AF＝BE＋DF.
3．如图，在▱ABCD中，对角线AC，BD相交于点O，E是BD延长线上的点，且△ACE是等边三角形．(1)求证：四边形ABCD是菱形；
证明：∵四边形ABCD是平行四边形，∴AO＝CO.又∵△ACE是等边三角形，∴EO⊥AC，即DB⊥AC，∴四边形ABCD是菱形．
(2)若∠AED＝2∠EAD，求证：四边形ABCD是正方形．
4．如图，在△ABC中，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得到△CFE.(1)求证：四边形ADCF是平行四边形；
证明：∵△CFE是由△ADE绕点E旋转180°得到的，∴点A、E、C三点共线，点D、E、F三点共线，且AE＝CE，DE＝FE，∴四边形ADCF是平行四边形．
(2)当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．
解：当∠ACB＝90°，AC＝BC时，四边形ADCF是正方形．理由如下：在△ABC中，∵AC＝BC，点D是边AB的中点，∴CD⊥AB，即∠ADC＝90°.由(1)知，四边形ADCF是平行四边形，∴四边形ADCF是矩形．
5.【中考·青岛】已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连结CE，CF，OE，OF.(1)求证：△BCE≌△DCF；
证明：∵四边形ABCD是菱形，∴AB＝BC＝CD＝DA，∠B＝∠D.又∵E，F分别是AB，AD的中点，∴BE＝DF，∴△BCE≌△DCF.
(2)当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．
解：当AB⊥BC时，四边形AEOF是正方形．理由如下：连结BD. ∵AB⊥BC，∴菱形ABCD是正方形，∴∠BAD＝90°，AB＝AD.由O是AC的中点，易知O是BD的中点，∴OA＝OB＝OC＝OD.
6．如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，AN是△ABC外角的平分线，CE⊥AN，垂足为点E，连结DE交AC于点F.(1)求证：四边形ADCE为矩形；
(2)当△ABC满足什么条件时，四边形ADCE是正方形？并给出证明；
∴∠ACD＝∠CAD＝45°，∴AD＝CD.∵四边形ADCE为矩形，∴四边形ADCE为正方形．
解：在Rt△ACD中，由勾股定理，得AD2＋CD2＝AC2.∵AD＝CD，∴2AD2＝2，∴AD＝1，∴正方形ADCE的周长为4AD＝4.
7．如图，正方形ABCD中，点E、F、G、H分别在AB、BC、CD、DA上，且AE＝BF＝CG＝DH.(1)四边形EFGH是正方形吗？为什么？
解：四边形EFGH是正方形．∵四边形ABCD是正方形，∴∠A＝∠B＝∠C＝∠D＝90°，AB＝BC＝CD＝DA.∵AE＝BF＝CG＝DH，∴AH＝BE＝CF＝DG.
∴∠BEF＋∠AEH＝90°，∴∠HEF＝90°，∴四边形EFGH是正方形．
(2)若正方形ABCD的边长为4 cm，且BE＝CF＝DG＝AH＝1 cm，请求出四边形EFGH的面积．
解：∵正方形ABCD的边长为4 cm，且BE＝CF＝DG＝AH＝1 cm，∴AE＝BF＝CG＝DH＝3 cm，∴四边形EFGH的面积＝EH2＝AH2＋AE2＝12＋32＝10(cm2)．
8．【中考·玉林】如图，在△ABC中，∠ACB＝90°，AC＝BC＝4，D是AB的中点，E，F分别是AC，BC上的点(点E不与端点A，C重合)，且AE＝CF，连结EF并取EF的中点O，连结DO并延长至点G，使GO＝OD，连结GE，GF，DE，DF.(1)求证：四边形EDFG是正方形；
∵∠ADC＝∠ADE＋∠EDC＝90°，∴∠EDC＋∠CDF＝∠EDF＝90°.∴四边形EDFG是正方形．
(2)当点E在什么位置时，四边形EDFG的面积最小？并求四边形EDFG面积的最小值．
解：过点D作DE′⊥AC于E′.∵四边形EDFG是正方形，∴S四边形EDFG＝DE2.∵△ABC为等腰直角三角形，∠ACB＝90°，AC＝BC＝4，∴易得∠DCE′＝∠A＝∠E′DA＝∠E′DC＝45°，∴点E′为AC的中点．