沪科版19.4 综合与实践 多边形的镶嵌习题ppt课件

这是一份沪科版19.4 综合与实践 多边形的镶嵌习题ppt课件，共16页。PPT课件主要包含了答案显示，核心必知，一个周角，既无缝隙又不重叠，见习题，4n＋2，答案B等内容，欢迎下载使用。
(1)18　(2)(4n＋2)
1．用形状相同或不同的平面封闭图形，覆盖平面区域，使图形间__________________地全部覆盖，在几何里面叫做平面镶嵌．
2．平面镶嵌的条件：要实现平面图形的镶嵌，必须保证每一个拼接点处的几个内角恰好能拼成__________．(无缝隙、不重叠)
1．【2021·铜仁改编】用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌．工人师傅用形状、大小完全相同的一种地砖在平整的地面上镶嵌，下列形状的地砖不能使用的是(　　)A．等边三角形 B．正方形C．正五边形 D．正六边形
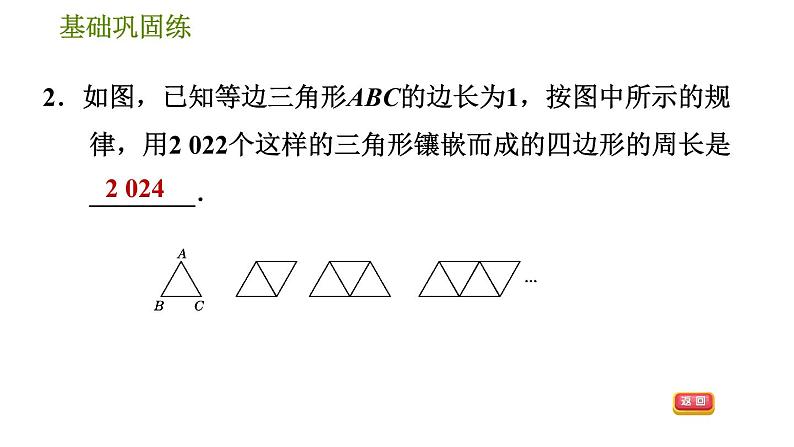
2．如图，已知等边三角形ABC的边长为1，按图中所示的规律，用2 022个这样的三角形镶嵌而成的四边形的周长是________．
3．用一种正多边形地砖铺满地面的条件是(　　)A．内角是整数度数 B．边数是3的倍数C．内角整除180° D．内角整除360°
4．用黑白两种颜色的正六边形地砖按如图所示的规律，拼成若干个图案：(1)第4个图案中有白色地砖________块；(2)第n个图案中有白色地砖________块．
5．用正三角形和正六边形作平面镶嵌，若每一个顶点周围有m个正三角形，n个正六边形，则m，n满足的关系式是(　　)A．2m＋3n＝12 B．m＋n＝8C．2m＋n＝6 D．m＋2n＝6
6．用三块正多边形的木板铺地，拼在一起并相交于一点的各边完全吻合，其中两块木板的边数都是8，则第三块木板的边数是(　　)A．4 B．5 C．6 D．8
7．利用边长相等的正三角形和正六边形的地砖镶嵌地面时，在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0)，则a＋b的值为(　　)A．3或4 B．4或5 C．5或6 D．4
【点拨】正三角形和正六边形的内角度数分别为60°、120°，60°×4＋120°＝360°，或60°×2＋120°×2＝360°，∴a＝4，b＝1或a＝2，b＝2，当a＝4，b＝1时，a＋b＝5；当a＝2，b＝2时，a＋b＝4.
8．如图，有四种正多边形(所有正多边形的边长相等)．(1)请你用其中两种进行平面镶嵌，有几种选择？是哪几种？
解：有两种选择：正三角形和正方形，正三角形和正六边形．
(2)若用两种正多边形进行平面镶嵌，p，q表示这两种正多边形的个数，x°，y°表示对应正多边形的每个内角的度数，则有方程px＋qy＝360，求(1)中每种平面镶嵌中p，q的值．