冀教版八年级下册数学 期末复习专题练 专题6.四边形（提升） 习题课件

这是一份冀教版八年级下册数学 期末复习专题练 专题6.四边形（提升） 习题课件，共45页。

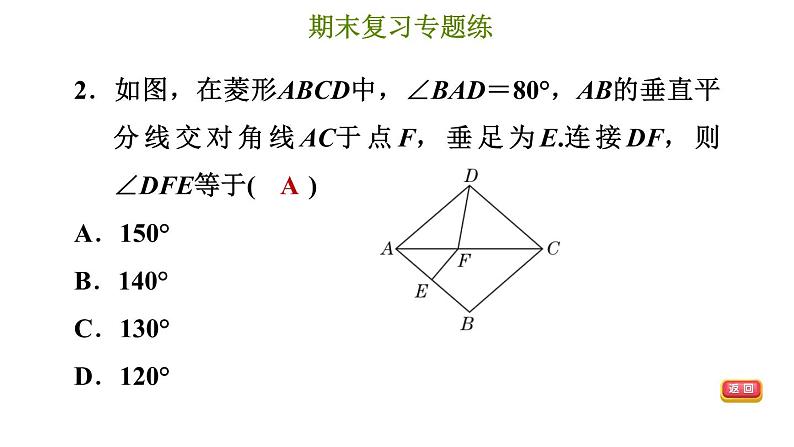
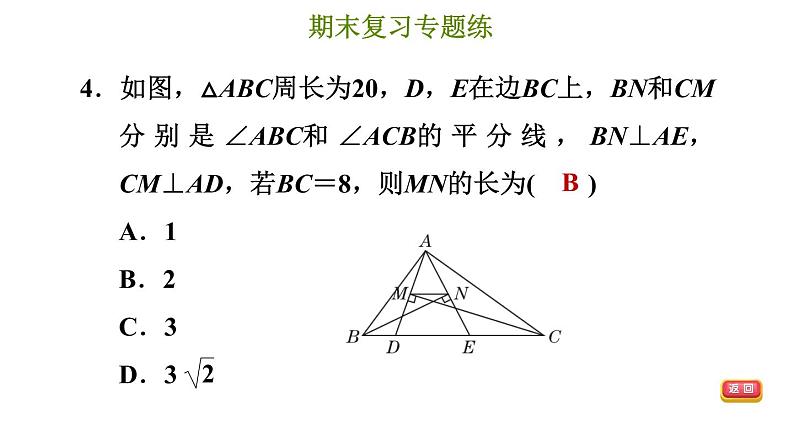
专题六 四边形（提升） 冀教版 八年级下期末复习专题练123467ADBDB答案显示5BD8B9C10B1112540°13142或6答案显示15见习题16见习题17见习题18见习题19见习题20°1．平行四边形一边长是10 cm，那么它的两条对角线的长度可以是(　　)A．8 cm和6 cm B．8 cm和8 cmC．8 cm和12 cm D．8 cm和16 cmDA2．如图，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，垂足为E.连接DF，则∠DFE等于(　　)A．150° B．140° C．130° D．120°3．【2020·河北邢台模拟】证明：平行四边形的对角线互相平分．已知：如图，四边形ABCD是平行四边形，对角线AC、BD相交于点O.求证：OA＝OC，OB＝OD.证明：∵四边形ABCD是平行四边形，∴…∴∠ABO＝∠CDO，∠BAO＝∠DCO.∴△AOB≌△COD.∴OA＝OC，OB＝OD.其中，在“四边形ABCD是平行四边形”与“∠ABO＝∠CDO，∠BAO＝∠DCO”之间应补充的步骤是(　　)A．AB＝CD，AD＝BC B．AD∥BC，AD＝BCC．AB∥CD，AD∥BC D．AB∥CD，AB＝CDD4．如图，△ABC周长为20，D，E在边BC上，BN和CM分别是∠ABC和∠ACB的平分线，BN⊥AE，CM⊥AD，若BC＝8，则MN的长为(　　)A．1 B．2 C．3 D．3 B5．将若干个大小相等的正五边形排成环状，如图所示是前3个五边形，要完成这一圆环还需正五边形的个数是(　　)A．6 B．7 C．8 D．9B6．如图，在△ABC中，∠BAC＝90°，AB＝6，AC＝8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则PM的最小值为(　　)A．5 B．2.5 C．4.8 D．2.4【答案】D7．如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DH⊥BC于点H，连接OH，若OA＝4，S菱形ABCD＝24，则OH的长为(　　)B8．如图，将边长为2 cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分的面积为1 cm2，则它移动的距离AA′等于(　　)A．0.5 cm B．1 cm C．1.5 cm D．2 cmB9．如图，AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF，交AD于点G，则下列结论：①DF＋AE>AD；②BE＝DE；③AD⊥EF；④AB∶AC＝BD∶CD.正确的有(　　)A．1个 B．2个 C．3个 D．4个【点拨】∵AD平分∠BAC，∴∠BAD＝∠CAD，∵DE⊥AB，DF⊥AC，AD＝AD，∴△AED≌△AFD，∴DE＝DF.在△ADE中，AE＋DE>AD，∴DF＋AE>AD，故①正确；∵∠B不一定是45°，∴∠B不一定等于∠BDE，【答案】C10．【2020·河北沙河模拟】如图①，图②，在给定的一张矩形纸片上作一个正方形，甲、乙两人的作法如下：甲：以点A为圆心，AD长为半径画弧，交AB于点E，以点D为圆心，AD长为半径画弧，交CD于点F，连接EF，则四边形AEFD即为所求；乙：作∠DAB的平分线，交CD于点M，同理作∠ADC的平分线，交AB于点N，连接MN，则四边形ADMN即为所求．对于以上两种作法，可以做出的判定是(　　)A．甲正确，乙错误 B．甲、乙均正确C．乙正确，甲错误 D．甲、乙均错误【点拨】由甲的作法可得DF＝AD＝AE.∵四边形ABCD是矩形，∴AB∥DC，∠A＝90°.∵DF∥AE，∴四边形AEFD是平行四边形．∵∠A＝90°，∴平行四边形AEFD是矩形．∵AD＝AE，∴矩形AEFD是正方形，故甲的作法正确；∵四边形ABCD是矩形，∠CDA＝∠DAB＝90°.【答案】B∵DM∥AN，∴四边形ANMD是平行四边形．∵∠DAB＝90°，∴平行四边形ANMD是矩形．∵AD＝AN，∴矩形ANMD是正方形，故乙的作法正确．故选B.11．【2020·河北唐山迁西县期末】如图，∠1＋∠2＋∠3＋∠4＋∠5＝________．540°12．如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于点H，连接OH，若∠DHO＝20°，则∠HDB的度数是________．20°13．如图，在矩形ABCD中，AB＝8，BC＝6，点P为边AB上任意一点，过点P作PE⊥AC，PF⊥BD，垂足分别为E，F，则PE＋PF＝________．14．如图，在等边三角形ABC中，BC＝6 cm，射线AG∥BC，点E从点A出发，沿射线AG以1 cm/s的速度运动，点F从点B出发，沿射线BC以2 cm/s的速度运动．如果点E，F同时出发，设运动时间为t (s)，当t＝________s时，以A，C，E，F为顶点的四边形是平行四边形．【点拨】①当点F在C的左侧时，根据题意得，AE＝t cm，BF＝2t cm，则CF＝BC－BF＝6－2t(cm)．∵AG∥BC，∴当AE＝CF时，四边形AECF是平行四边形，即t＝6－2t，解得t＝2；②当点F在C的右侧时，根据题意得，AE＝t cm，BF＝2t cm，则CF＝BF－BC＝2t－6(cm)．∵AG∥BC，∴当AE＝CF时，四边形AEFC是平行四边形，即t＝2t－6，解得t＝6.综上可得，当t＝2或t＝6时，以A，C，E，F为顶点的四边形是平行四边形．【答案】2或615．(10分)【2019·河北唐山丰南区二模】关于n边形，甲、乙、丙三位同学有以下三种说法：甲：五边形的内角和为520°；乙：正六边形每个内角为130°；丙：七边形共有对角线14条．判断三种说法是否正确，并对其中你认为不对的说法用计算进行说明．解：甲、乙的说法不正确；丙的说法正确．甲：正五边形的内角和为180°×(5－2)＝540°；乙：正六边形外角和为360°，每个外角为360°÷6＝60°，每个内角为180°－60°＝120°.16．(10分)已知，△ABC、△ADE是等腰三角形，AB＝AC，AD＝AE，D是BC上一点，∠DAE＝∠BAC，过点E作BC的平行线交AB于点F，连接CF、DE.(1)如图①，求证：四边形CDEF是平行四边形；∵EF∥BC，∴∠ABC＝∠EFB.∴∠ABE＝∠EFB，∴EB＝EF，∴EF＝CD.∵EF∥BC，∴四边形CDEF是平行四边形．(2)如图②，连接BE、DF，若AD⊥BC，在不添加任何辅助线的情况下，请直接写出图②中长度等于BC长的 的线段．17.(12分)如图，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H.(1)求证：△EAB≌△GAD；证明：∵四边形ABCD、四边形AGFE是正方形，∴AB＝AD，AE＝AG，∠DAB＝∠EAG，∴∠EAB＝∠GAD.在△EAB和△GAD中，(2)若AB＝3 ，AG＝3，求EB的长．18．(12分)如图①，AB∥CD，点E，F分别在AB，CD上，连接EF.∠AEF，∠CFE的平分线交于点G，∠BEF，∠DFE的平分线交于点H.(1)求证：四边形EGFH是矩形；(2)小明在完成(1)的证明后继续进行了探索．过G作MN∥EF，分别交AB，CD于点M，N，过H作PQ∥EF，分别交AB，CD于 P，Q，得到四边形MNQP.此时，他猜想四边形MNQP是菱形．请在图②中补全他的证明思路．证明：FG平分∠CFE；GE＝FH；∠GME＝∠FQH；∠GEF＝∠EFH(部分空答案不唯一)19．(14分)如图，在Rt△ABC中，∠ACB＝90°，过点C作直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，垂足为F，交直线MN于点E，连接CD，BE.(1)求证：CE＝AD；证明：∵DE⊥BC，∴∠DFB＝90°.∵∠ACB＝90°，∴∠ACB＝∠DFB.∴AC∥DE. 又∵MN∥AB，即CE∥AD，∴四边形ADEC是平行四边形，∴CE＝AD.(2)当D为AB的中点时，四边形BECD是什么特殊四边形？说明你的理由；解：四边形BECD是菱形．理由：∵D为AB的中点，∴AD＝BD.∵CE＝AD，∴BD＝CE.∵BD∥CE，∴四边形BECD是平行四边形．∵DE⊥BC，∴四边形BECD是菱形．(3)若D为AB的中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明理由．解：当∠A＝45°时，四边形BECD是正方形．理由：∵∠ACB＝90°，∠A＝45°，∴∠ABC＝45°＝∠A. ∴AC＝BC.∵D为AB的中点，∴CD⊥AB.∴∠CDB＝90°. ∴菱形BECD是正方形．