华师版八年级下册数学 第19章 19.2.3 菱形性质和判定的综合应用 习题课件

这是一份华师版八年级下册数学 第19章 19.2.3 菱形性质和判定的综合应用 习题课件，共24页。

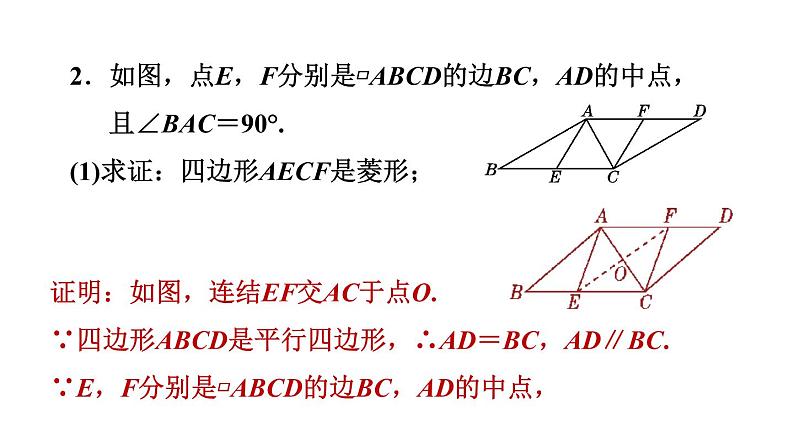
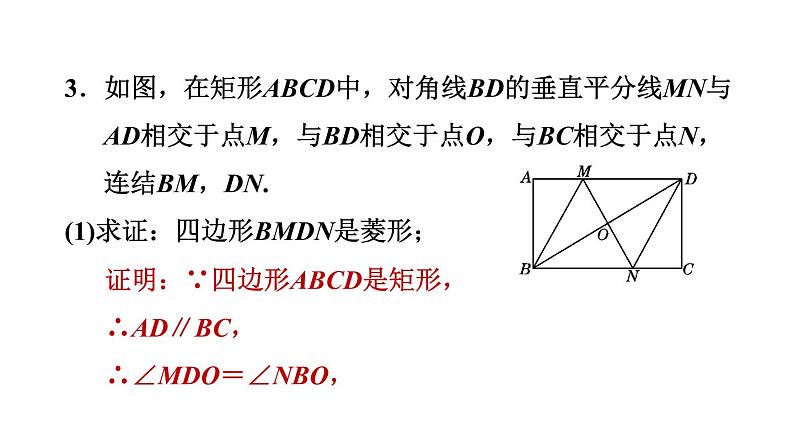
第19章　矩形、菱形与正方形 华师版 八年级下19.2　菱形第3课时 菱形性质和判定的综合应用答案显示1234见习题5见习题见习题见习题见习题678见习题见习题见习题1．如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE∥BD，过点D作ED∥AC，AE与ED相交于点E.(1)求证：AE＝DE；解：如图，连结OE.∵四边形AODE是菱形，∴AE＝AO.由(1)知AO＝OB，∴AE＝OB.又∵AE∥BD，∴四边形AEOB是平行四边形．∵BE⊥ED，ED∥AC，∴BE⊥AC，∴四边形AEOB是菱形，∴AB＝OB，∴AB＝OB＝OA，∴△AOB是等边三角形，∴∠AOB＝60°，∴∠AOD＝180°－60°＝120°.(2)连结BE，交AC于点F.若BE⊥ED，求∠AOD的度数．2．如图，点E，F分别是▱ABCD的边BC，AD的中点，且∠BAC＝90°.(1)求证：四边形AECF是菱形；证明：如图，连结EF交AC于点O.∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC.∵E，F分别是▱ABCD的边BC，AD的中点，(2)若∠B＝30°，求∠ACF的度数．解：∵∠BAC＝90°，∠B＝30°，∴∠ACE＝60°.由(1)知，四边形AECF是菱形，∴∠ACF＝∠ACE＝60°.3．如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连结BM，DN.(1)求证：四边形BMDN是菱形；证明：∵四边形ABCD是矩形，∴AD∥BC，∴∠MDO＝∠NBO，(2)若AB＝6，AD＝8，求菱形BMDN的面积和对角线MN的长．4．【2021·南京鼓楼区月考】如图，平行四边形ABCD的对角线交于点O，以OD，CD为邻边作平行四边形DOEC，OE交BC于点F，连结BE.(1)求证：F为BC的中点；证明：∵四边形ABCD是平行四边形，∴OB＝OD，∵四边形DOEC为平行四边形，∴OD∥EC，OD＝EC，∴EC∥OB，EC＝OB，∴四边形OBEC为平行四边形，∴BF＝CF，即F是BC的中点．解：∵四边形ABCD是平行四边形，OB⊥AC，∴▱ABCD是菱形，∵四边形OBEC为平行四边形，OB⊥AC，∴▱OBEC是矩形，∴BC＝OE＝2OF，∵OF＝2，∴BC＝4，∴四边形ABCD的周长＝4BC＝16.(2)若OB⊥AC，OF＝2，求四边形ABCD的周长．5．【中考·南宁】如图，在▱ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE＝DF.(1)求证：▱ABCD是菱形；证明：∵四边形ABCD是平行四边形，∴∠B＝∠D.∵AE⊥BC，AF⊥CD，∴∠AEB＝∠AFD＝90°.在△AEB和△AFD中，(2)若AB＝5，AC＝6，求▱ABCD的面积．6．【中考·滨州】如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连结CG.(1)求证：四边形CEFG是菱形；证明：由题意可得△BCE≌△BFE，∴∠BEC＝∠BEF，FE＝CE. ∵FG∥CE，∴∠FGE＝∠CEB，∴∠FGE＝∠FEG，∴FG＝FE，∴FG＝EC，∴四边形CEFG是平行四边形．∴四边形CEFG是菱形．(2)若AB＝6，AD＝10，求四边形CEFG的面积．7．如图，在四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E.(1)求证：四边形AECD是菱形；证明：∵AB∥CD，CE∥AD，∴四边形AECD是平行四边形，∠DAC＝∠ACE.∵AC平分∠BAD，∴∠EAC＝∠DAC，∴∠EAC＝∠ACE，∴AE＝EC，∴四边形AECD是菱形．(2)若点E是AB的中点，试判断△ABC的形状，并说明理由．解：△ABC是直角三角形．理由如下：∵点E是AB的中点，∴AE＝BE.∵AE＝CE，∴CE＝BE，∴∠EBC＝∠ECB.又∵∠EBC＋∠BCE＋∠ACE＋∠BAC＝180°,∠EAC＝∠ACE，∴∠BCE＋∠ECA＝90°，即∠BCA＝90°，∴△ABC是直角三角形．8．【中考·湘潭】如图，将△ABC沿着AC边翻折，得到△ADC，且AB∥CD.(1)判断四边形ABCD的形状，并说明理由；解：四边形ABCD是菱形．理由如下：∵将△ABC沿着AC边翻折，得到△ADC，∴AB＝AD，BC＝CD，∠BAC＝∠DAC，∠BCA＝∠DCA.∵AB∥CD，∴∠BAC＝∠DCA，∴∠BAC＝∠DAC＝∠BCA＝∠DCA，∴AB＝AD＝BC＝CD，∴四边形ABCD是菱形．(2)若AC＝16，BC＝10，求四边形ABCD的面积．