- 20.2-2一次函数的图像 教案 教案 5 次下载
- 20.2-1一次函数的图像 教案 教案 5 次下载
- 20.3-2一次函数的性质 教案 教案 5 次下载
- 20.3-1一次函数的性质 教案 教案 5 次下载
- 20.4-2一次函数的应用 教案 教案 5 次下载
2021学年20.2 一次函数的图像获奖教案
展开__月__日 星期__ 第_1_周
课 题 | 20.2-3一次函数的图像 | 课 型 | 新授 | 教 时 | 1 | |
教 学 目 标 | 1. 借助一次函数,进一步认识一元一次方程、一元一次不等式的解的情况; | |||||
2. 理解一次函数与一元一次方程、一元一次不等式之间的关系; | ||||||
3. 领会数形结合的数学思想,初步能用函数知识分析问题和解决问题。 | ||||||
重 点 | 能以函数观点认识一元一次方程、一元一次不等式的解; | |||||
难 点 | 能以函数观点认识一元一次方程、一元一次不等式的解. | |||||
教具准备 | 多媒体课件 | |||||
教 学 过 程 | ||||||
教师活动 | 学生活动 | |||||
一、 复习 1.两条直线截距相同则经过同一点(0,),直线的倾斜程度由 决定;直线的平移;两条直线平行的条件 2.完成课件课前练习题
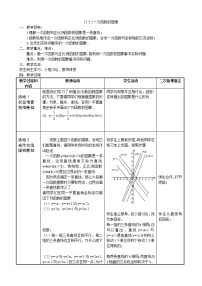
二、新授 : (一)思考: 1.一元一次方程kx+b=0的根与一次函数y=kx+b的图像与x轴交点的横坐标之间的关系. 2.观察如图,直线经过点A(0,-1),B(2,0) (1)轴上方直线上的点的纵坐标有什么特点? 轴下方直线上的点的纵坐标有什么特点? (2)直线上的点的横坐标取何值时,这些点在轴上方? 直线上的点的横坐标取何值时,这些点在轴下方? 从另一个角度思考:设直线上的点的坐标为 当直线上的点位于轴上方时,,即,解得 当直线上的点位于轴上方时,,即,解得 所以直线在轴上方的点的横坐标,直线在轴下方的点的横坐标
(二)归纳: 1.一次函数与一元一次方程的关系 一次函数 y=kx+b的图像与x轴交点的横坐标就是一元一次方程kx+b=0的解;反之,一元一次方程kx+b=0的解就是一次函数 y=kx+b的图像与x轴交点的横坐标. 2.一次函数与一元一次不等式的关系 由一次函数 y=kx+b的函数值y大于0(或小于0),就得到关于x的一元一次不等式kx+b>0(或kx+b<0).在一次函数 y=kx+b的图像上且位于x轴上方(或下方)的所有点,它们的横坐标的取值范围就是不等式kx+b>0(或kx+b<0)的解.
(三)例题示范: 例6:已知函数. (1)当x取何值时,函数值y=5? (2)当x取何值时,函数值y>5? (3)在平面直角坐标系xOy中,在直线上且位于x轴下方的所有点,它们的横坐标的取值范围是什么? 解:(1)要使函数的值y=5,只要使. 解方程,得.所以当时,函数值. (2) 要使函数的值,只要使. 解不等式,得.所以当时,函数值. (3)因为所求的点在直线上且位于x轴下方, 所以. 解得, 即所有这样的点的横坐标的取值范围是小于的一切实数.
三、练习: P11/1-3
四、小结: 一次函数与一元一次方程、一元一次不等式之间的关系
五、作业: 练习册:习题20.2-3 |
回答问题,回顾、复习旧知
学生通过具体事例探讨一元一次不等式的解集与一次函数图像之间的关系 从图像中获得信息,感知结论,形成理性认识
把所获得的具体结论进行一般化总结
(1)(2)从代数角度思考,通过式的代换解决问题 (3)从图形角度探讨,加深一元一次方程、一元一次不等式、一次函数三者的关系的认识
完成练习
谈收获和注意点 | |||||
举例板书设计: 1. 一次函数与一元一次方程、一元一次不等式之间的关系. 2.例题解题格式 | ||||||
课后反思:
| ||||||
初二数学一次函数的图像教案: 这是一份初二数学一次函数的图像教案,共5页。
人教版八年级下册19.2.2 一次函数教案: 这是一份人教版八年级下册19.2.2 一次函数教案,共12页。教案主要包含了知识梳理,课堂精讲,课后巩固练习等内容,欢迎下载使用。
人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数教案设计: 这是一份人教版八年级下册第十九章 一次函数19.2 一次函数19.2.2 一次函数教案设计,共5页。教案主要包含了教学目的,教学重点,教学难点,教学过程等内容,欢迎下载使用。