数学沪教版 (五四制)22.5 等腰梯形优秀课件ppt

这是一份数学沪教版 (五四制)22.5 等腰梯形优秀课件ppt，共17页。PPT课件主要包含了等腰梯形有哪些性质，证一证，方法二，下一页，方法一，则∠B∠DEC，∴ABDE，∴∠B∠C等内容，欢迎下载使用。
一、巩固旧知、引出新知
口答：(1) 什么叫梯形？(2) 什么叫等腰梯形？(3)等腰梯形的表达式：
二、验证猜想、形成定理
1.从边来考虑:根据等腰梯形的定义具有___________________
两腰相等、底边互相平行
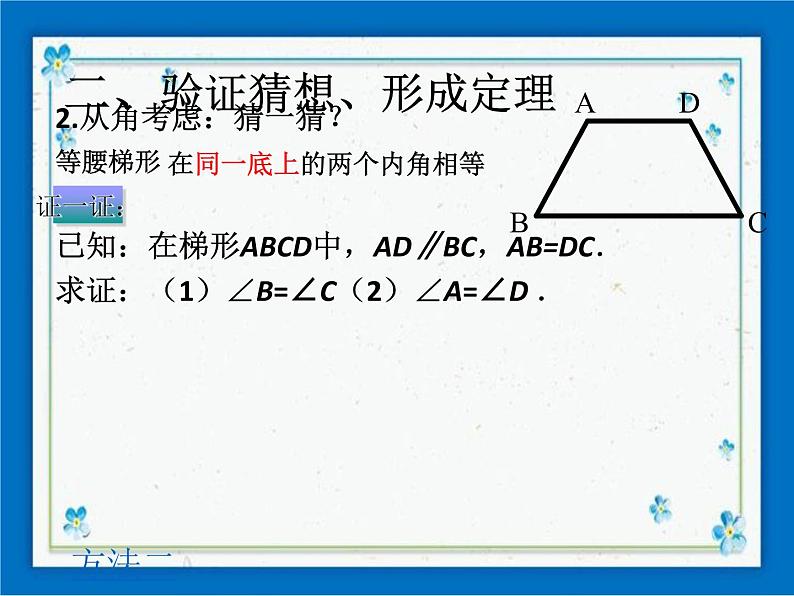
2.从角考虑：猜一猜？等腰梯形已知：在梯形ABCD中，AD∥BC，AB=DC．求证：（1）∠B=∠C（2）∠A=∠D ．
在同一底上的两个内角相等
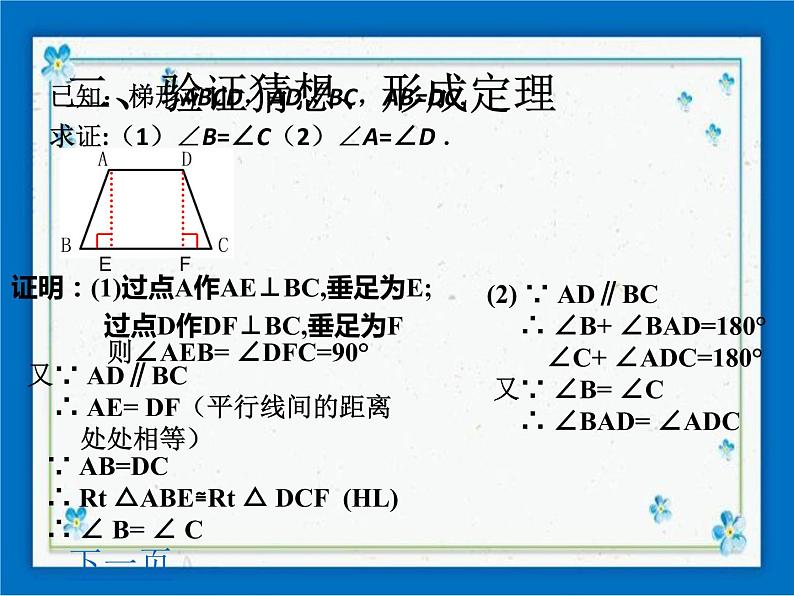
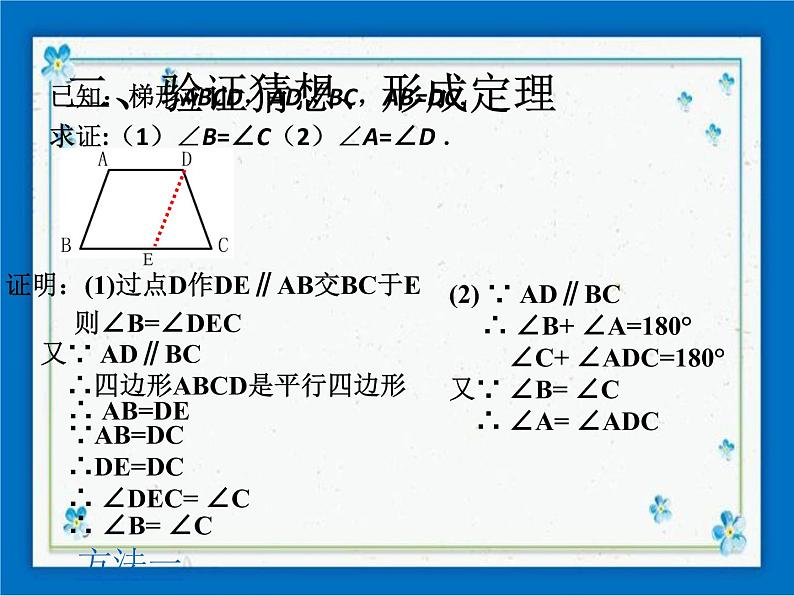
已知：梯形ABCD，AD∥BC，AB=DC．求证:（1）∠B=∠C（2）∠A=∠D ．
证明：(1)过点A作AE⊥BC,垂足为E; 过点D作DF⊥BC,垂足为F
则∠AEB= ∠DFC=90°
又∵ AD∥BC ∴ AE= DF（平行线间的距离 处处相等）
∵ AB=DC∴ Rt △ABE≌Rt △ DCF (HL)∴ ∠ B= ∠ C
(2) ∵ AD∥BC ∴ ∠B+ ∠BAD=180° ∠C+ ∠ADC=180° 又∵ ∠B= ∠C ∴ ∠BAD= ∠ADC
证明：(1)过点D作DE∥AB交BC于E
又∵ AD∥BC ∴四边形ABCD是平行四边形
∵AB=DC∴DE=DC∴ ∠DEC= ∠C
(2) ∵ AD∥BC ∴ ∠B+ ∠A=180° ∠C+ ∠ADC=180°又∵ ∠B= ∠C ∴ ∠A= ∠ADC
二、验证猜想、形成定理
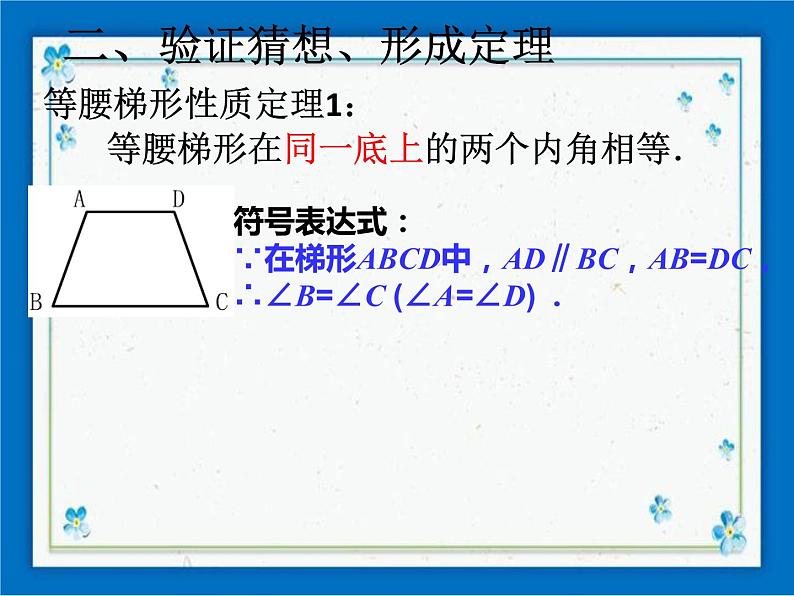
等腰梯形性质定理1： 等腰梯形在同一底上的两个内角相等．
符号表达式：∵在梯形ABCD中，AD∥BC，AB=DC，∴∠B=∠C (∠A=∠D) ．
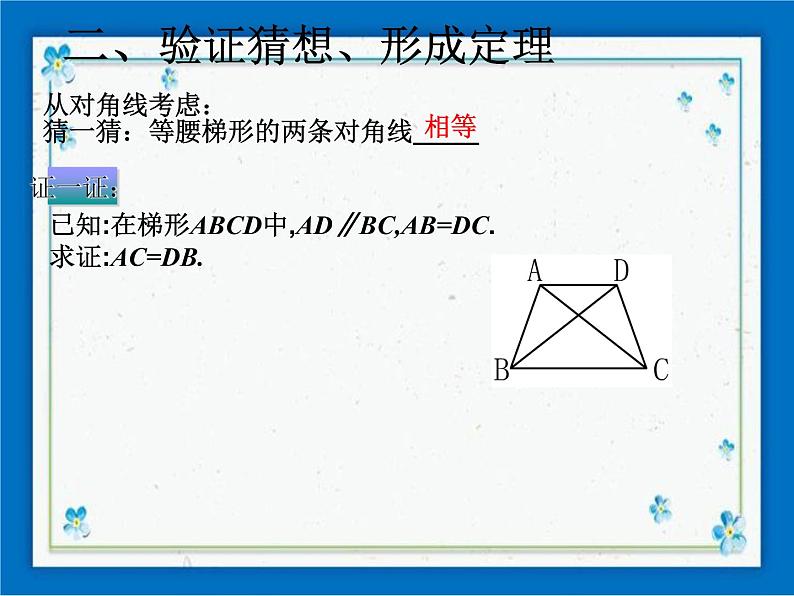
从对角线考虑：猜一猜：等腰梯形的两条对角线_____
已知:在梯形ABCD中,AD∥BC,AB=DC.求证:AC=DB.
等腰梯形性质定理2： 等腰梯形的两条对角线相等．
符号表达式：∵在梯形ABCD中，AD∥BC，AB=DC，∴AC=DB．
三、应用定理、深化认知
例1 .已知：如图，等腰梯形ABCD中，AD∥BC,腰BA和CD的延长线相交于点E.求证：⊿EAD是等腰三角形.
作∠BEC的平分线，交AD于M，交BC于N，则它既垂直平分AD，又垂直平分BC即∠BEC的平分线所在的直线经过AD的中点M和BC的中点N.由等腰三角形是轴对称图形 ，对称轴是两底的中点的连线所在的直线
因此等腰梯形也是轴对称图形.
4.例题讲解，熟悉新知：
例2 ．如图：等腰梯形ABCD中，AD∥ BC，AB=CD，延长BC使CE=AD，并连接DE ．求证：BD=DE ．
证明:∵梯形ABCD中，AD∥ BC，AB=CD.∴∠BAD=∠ADC ∠ADC=∠DCE∴∠BAD =∠DCE∵AB=CD,AD=CE∴△ABD≌△CDE∴BD=DE
四、小结梳理、布置作业
畅所欲言：谈谈你今天学到了什么
四、应用定理，深化认知：
1．如图,在等腰梯形ABCD,AD∥BC,AD=AB, BD⊥DC.则∠C=______.
2. 等腰梯形ABCD中，AD∥BC,AB=CD,∠ABC=60°，AD=15，AB=45，求BC的长 ．
等腰梯形ABCD中，AD∥ BC，AB=CD，延长BC使CE=AD，并连接DE．求证：BD=DE ．等腰梯形ABCD的面积和等腰三角形DBE的面积有什么关系？
证明:∵ △ABD≌△CDE ∴S△ABD=S △CDE
又∵S梯形ABCD =S △ABD+S △BCD S △ DBE =S △CDE+S △BCD
∴ S梯形ABCD = S △ DBE