2020-2021学年度河南周口川汇区上期期中统考试卷人教版九年级数学（试卷+答案）

这是一份2020-2021学年度河南周口川汇区上期期中统考试卷人教版九年级数学（试卷+答案），共12页。

得分
评卷人
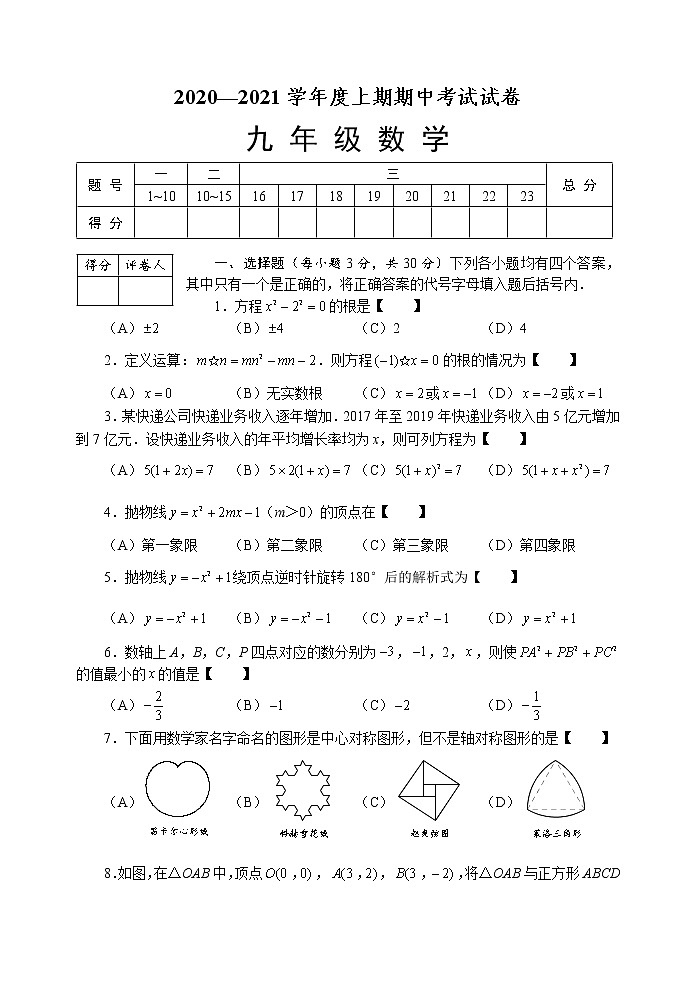
一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内．
1．方程的根是【 】
（A）（B）（C）2（D）4
2．定义运算：．则方程的根的情况为【 】
（A）（B）无实数根（C）或（D）或
3．某快递公司快递业务收入逐年增加．2017年至2019年快递业务收入由5亿元增加到7亿元．设快递业务收入的年平均增长率均为x，则可列方程为【 】
（A）（B）（C）（D）
4．抛物线（m＞0）的顶点在【 】
（A）第一象限（B）第二象限（C）第三象限（D）第四象限
5．抛物线绕顶点逆时针旋转180°后的解析式为【 】
（A）（B）（C）（D）
6．数轴上A，B，C，P四点对应的数分别为，，2，，则使的值最小的的值是【 】
（A）（B）（C）（D）
7．下面用数学家名字命名的图形是中心对称图形，但不是轴对称图形的是【 】
（A）笛卡尔心形线
（B）科赫雪花线
（C）赵爽弦图
（D）莱洛三角形
8．如图，在△OAB中，顶点，，，将△OAB与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转90°，则第2021次旋转结束时，点D的坐标为【 】
（A）（B）（C）（D）
（第8题）
A
B
C
D
O
y
x
（第9题）
A
B
O
C
D
（第10题）
A
x
y
O
B
9．如图，点C，D在半圆O上，CO∥BD，，，则，满足的关系是【 】
（A）（B）（C）（D）
10．如图，直线与抛物线交于点A，B，并且点A，B关于原点O对称．则的值是【 】
（A）（B）（C）（D）
得分
评卷人
二、填空题（每小题3分，共15分）
11．写出一个两根为，2的一元二次方程________________．
12．已知抛物线与x轴有两个交点，则m的取值范围是__________．
13．如图，线段AB，CD的端点都在格点上，其中一条线段可以认为是由另一条线段绕着某定点旋转一定的角度得到的，则该定点的坐标为____________．
（第14题）
O
x
A
B
C
y
P
（第13题）
y
B
A
D
C
x
O
（第15题）
A
B
C
F
E
D
14．如图，抛物线与坐标轴交于A，B，C三点，则经过三个交点的圆的圆心坐标为__________．
15．如图，在菱形ABCD中，，，以点C为顶点，在菱形内部作等边△CEF，连接AE，AF，则△AFE的周长的最小值等于_______．
三、解答题（本大题共8个小题，满分75分）
16．（8分）得分
评卷人
已知关于x的一元二次方程．
⑴ 当时，求方程的根；
⑵ 若方程存在实数根，求实数的取值范围．
得分
评卷人
17．（9分）某商品现在的售价为每件65元，每周可卖出300件．适逢换季，商场为避免商品积压决定降价促销．市场调查反映：每降价1元，每周可多卖出20件．已知商品的进价为每件40元，如何定价才能使利润最大？最大利润是多少？
得分
评卷人
18．（9分）已知点P在第一象限内的二次函数的图象上，PA⊥x轴于点A，点，连接PO，PB．
⑴ 求的值；
⑵ 求的最小值．
y
O
P
A
B
x
19．（9分）得分
评卷人
画图并回答问题（不写画法，保留画图痕迹）．
已知：如图，点O和线段AB．
⑴ 画出线段AB绕点O逆时针旋转90°后的线段A1B1；
⑵ 画出与线段AB关于点O对称的线段A2B2；
⑶ 连接A1B，A2B1，直接判断线段A1B，A2B1的位置关系和大小关系．
A
B
O
A1
B1
B2
A2
得分
评卷人
20．（9分）如图，AB是⊙O的直径，弦AC为8 cm，弦BC为6 cm，∠ACB的平分线交⊙O于点D．
⑴ 求AD的长；
⑵ 作DE⊥AC，垂足为点E，求DE的长．
A
B
C
E
D
O
E
21．（10分）如图，抛物线与x轴正半轴，y轴负半轴分别交于点A，B，且，点C为抛物线的顶点．
得分
评卷人
⑴ 求抛物线的解析式及点C的坐标；
⑵ 点M，N为抛物线上两点（点M在点N的左侧），且到对称轴的距离分别为2个单位长度和3个单位长度，点P为抛物线上点M，N之间（含点M，N）的一个动点，求点P的纵坐标yP的取值范围．
A
B
C
O
y
x
得分
评卷人
22．（10分）小亮在学习过程中遇到这样一个问题：
如图，在正方形ABCD中，cm，点E在BC边上，将线段EA绕点E顺时针旋转90°至EA′，与CD边交于点F，连接CA′．当时，求线段BE的长．
小亮尝试用学习函数的经验研究此问题．请将下面的探究过程补充完整：
⑴ 根据点E的不同位置画出相应的图形，测量线段BE，DF，CA′的长度，得到下表的几组对应值．
BE/cm
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
CA′/cm
0.0
1.4
2.8
4.2
5.7
7.1
8.5
9.9
11.3
DF/cm
8.0
7.1
6.5
6.1
a
6.1
6.5
7.1
8.0
O
1
2
3
4
5
7
6
8
x/cm
y/cm
1
2
3
4
5
6
7
8
9
10
11
12
上表中a的值是________．
⑵ 将线段BE的长度作为自变量x，CA′和DF的长度都是x的函数，请在平面直角坐标系xOy中画出函数的图象；
⑶ 结合函数图象直接写出：当时，线段BE长度的近似值（结果保留一位小数）．
A
D
B
E
C
A′
F
得分
评卷人
23．（11分）将正方形ABCD的边AB绕点A逆时针旋转至AB′，记旋转角为α，过点D作DE⊥BB′于点E，连接CE，以点B为端点，沿B′→E方向，在直线BB′上取点F，使，连接CF．
⑴ 当＜α＜时，如图1，△CEF的形状为__________________；
⑵ 当＜α＜时，如图2，⑴中的结论是否仍然成立？如果成立，请进行证明；如果不成立，请说明理由；
⑶ 若＜α＜且，当以点B′，E，C，D为顶点的四边形是平行四边形时，请直接写出的值．
图1
A
D
E
B′
F
B
C
A
D
E
B′
F
B
C
图2
2020—2021学年度上期期中考试试卷
九年级数学参考答案
一、选择题（每小题3分，共30分）
1．A；2．B；3．C；4．C；5．D；6．A；7．C；8．C；9．B；10．C
二、填空题（每小题3分，共15分）
11．；12．m＜1；13．，；14．；；15．．
三、解答题（本大题共8个小题，满分75分）
16．（10分）
原方程整理为．
⑴ 当时，，．或 ．
所以方程的根为或；
⑵ 若方程存在实数根，则△≥0．得≤．
所以，实数的取值范围是≤．
17．（9分）
设每件的售价为x元，则利润．
整理得．
当时，有最大值．
．
答：当定价为每件60元时，利润最大，最大利润为8000元．
18．（9分）
y
O
P
A
B
x
设，则．
．
所以．
⑴ ∵，∴；
⑵ ∵，
∴当O，P，B共线时，有最小值．
∵，∴的最小值为8．
19．（9分）
A
B
O
A1
B1
B2
A2
⑴ 如图，A1B1；
⑵ 如图，A2B2；
⑶ A1BA2B1，A1B⊥A2B1．
20．（10分）
A
B
C
E
D
O
E
⑴ ∵AB是⊙O的直径，∴．
∵AC8，BC6，∴．
∵CD平分，∴．
连接OD，∴．
∴．
⑵ 设，则．
在△ADE中，，即．
解得或（舍去）．
∴DE的长为7 cm．
21．（10分）
A
B
C
O
y
x
⑴ 设，则．代入，得．
∵，∴．
抛物线的解析式为．易知．
⑵ 对称轴为，点M的横坐标有两种情况，
即xM，3；
点N的横坐标为xN4．
∴xP的取值范围有两个．
即≤x≤4和3≤x≤4．
当≤x≤4时，≤yP≤5；
当 3≤x≤4时，0≤yP≤5．
22．（10分）
A
D
B
E
C
A′
F
O
1
2
3
4
5
7
6
8
x/cm
y/cm
1
2
3
4
5
6
7
8
9
10
11
12
⑴ 6.0；
⑵ 函数图象如图；
⑶ 不唯一， 4.1，4.2，4.3，4.4四数其一即可．
23．（11分）
图1
A
D
E
B′
F
B
C
A
D
E
B′
F
B
C
图2
⑴ 等腰直角三角形；
⑵ 成立．理由如下：
∵DE⊥BE，．
∴．
∴．
∵，，
∴△CBF≌△CDE（SAS）．
∴，．
∴．
∴△CEF是等腰直角三角形；
⑶ 3或1．