西师大版六年级下册比例精品ppt课件

这是一份西师大版六年级下册比例精品ppt课件，共24页。PPT课件主要包含了知识回顾，什么叫做比值，∶10，7∶45，∶45，情景创设，探索新知，比值相等，你是怎样判断的，因为6∶10＝06等内容，欢迎下载使用。

1.谁能说一说什么叫做比？
两个数相除又叫做两个数的比。
比的前项除以比的后项所得的商，叫做比值。
3.求一求下面各比的比值。
18∶45 = 18 ÷ 45 = 0.4
6∶10 = 6 ÷ 10 = 0.6
2.7∶4.5 = 2.7 ÷ 4.5 = 0.6
观察：6∶10和2.7∶4.5的比值有什么关系？
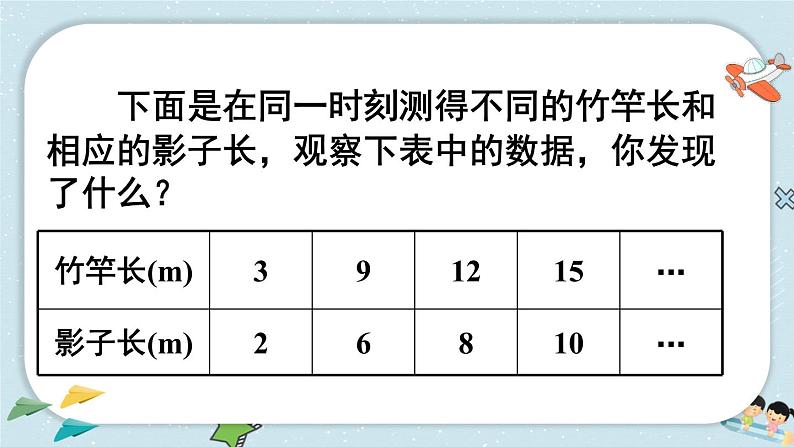
下面是在同一时刻测得不同的竹竿长和相应的影子长，观察下表中的数据，你发现了什么？
3∶2=1.5，9∶6=1.5。3∶2=9∶6，竹竿长与影子长的比值是相等的。
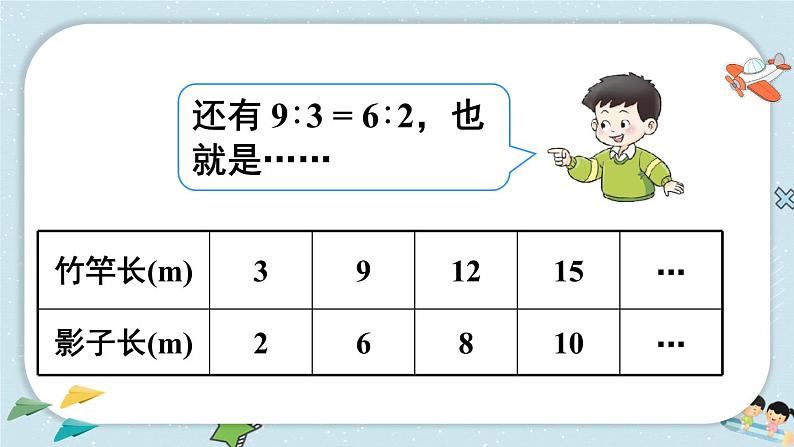
还有 9∶3 = 6∶2，也就是……
　　像这样的：3∶2=9∶6，9∶6=12∶8，12∶8=15∶10 …… 都是比例。
表示两个比相等的式子叫做比例。
　　有两个比且（ ），就能组成比例；反之，如果是比例，就一定有两个比，且（ ）。
2∶9 和 3∶6 能组成比例吗？
2∶5 和 80∶200 能组成比例吗？
2∶9和3∶6不能组成比例，因为它们的比值不相等。
2∶5和80∶200能组成比例，因为它们的比值相等。
下面哪组中的两个比可以组成比例？把能组成的比例写出来。
（1）6∶10和9∶15
（2）20∶5和1∶4
所以6∶10=9∶15
（3） 和6∶4
（4）0.6∶0.2和
你能用 2，3，6，9 组成一个比例吗？
3 ∶ 2 = 9 ∶ 6
组成比例的四个数，叫做比例的项。
在一个比例中，两端的两项叫做比例的外项，中间的两项叫做比例的内项。
3 ∶ 2 = 9 ∶ 6 也可以写成 。
1.2∶0.9=0.8∶0.6
将上面 4 个比例中的两个外项和两个内项分别相乘，你能发现什么？
2×6=123×4=122×6=3×4…
1.2×0.6＝0.720.9×0.8＝0.721.2×0.6＝0.9×0.8…
想一想，如果把比例写成分数形式，等号两端的分子和分母分别交叉相乘，它们的积有什么关系？
在一个比例中，两个外项的积等于两个内项的积，这叫做比例的基本性质。
如果 a:b=c:d（b、d≠0）
应用比例的基本性质，判断下面哪组中的两个比可以组成比例。
10∶20 和 0.5∶0.9
12∶4 和 24∶8
因为：10×0.9=9 20×0.5=10
所以： 10∶20 和 0.5∶0.9 不能组成比例。
因为： 12×8=96 4×24=96
所以：12∶4和24∶8可以组成比例。
1.两人一组，从右边10 张扑克牌中任意抽出 4 张，看牌上的数（A 代表1）能不能组成比例。
2.把 改写成比例，能写出哪些比例？先和同学讨论，再写出比例。