2020-2021学年3. 切线完美版教学课件ppt

这是一份2020-2021学年3. 切线完美版教学课件ppt，文件包含2723切线课件ppt、2723切线教学设计doc等2份课件配套教学资源，其中PPT共27页， 欢迎下载使用。
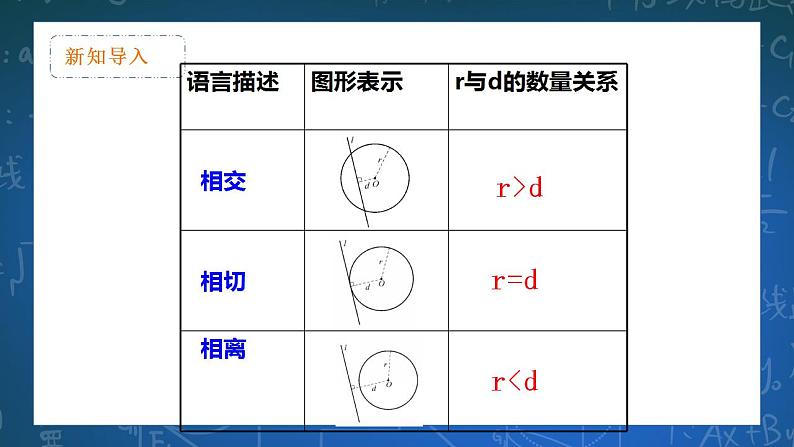
亲爱的同学们，上节课我们学习了直线与圆的位置关系，请同学们回忆一下.
下雨天，当你转动雨伞，你会发现雨伞上的水珠顺着伞面的边缘飞出。仔细观察一下，水珠是顺着什么样的方向飞出的？这就是我们所要研究的直线与圆相切的情况。
如图27.2.8，画一个圆O及半径OA，经过⊙O的半径OA的外端点A画一条直线l垂直于这条半 径OA，这条直线与圆有几个公共点？
从图27.2.8可以看出，对直线l上除点A外的任一 点P，必有OP＞OA，即点P位于圆外，从而可知直线与圆只有一个公共点，所以直线l是圆的切线!由此可得下 面判定切线的方法:
雨伞上的水珠就 是沿着切线方向向外飞出的。
切线的判定定理 ： 经过圆的半径的外端且垂直于这条半径的直线是圆的切线 。
能说出过圆上任意一点画圆的切线的方法吗 ?
如图27.2.9，直线l是☉O的切线， 点 A 为切点 ， 那么半径OA与l垂直吗？
由于l是☉O的切线， 圆心O到直线l 的距离等于半径，所以OA 是圆心O到直线l的距离，因此l⊥OA，有 ：
切线的性质定理：圆的切线垂直于经过切点的半径
如图，直线AB经过☉O 上的点A，且AB=OA，∠OBA=45° 求证：直线AB是☉O的切线。
证明：∵AB=OA，∠OBA=45°∴ ∠AOB= ∠OBA=45°∴ ∠OAB= 90°又∵点A在圆上，∴直线AB是☉O的切线（切线的判定定理 ）
判断一条直线是一个圆的切线有三个方法：
1.定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线;
2.数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；
3.判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线.
如图，PA 、PB为☉O 的两条切线，点A、B为切点，我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长。如图 线段PA、PB就是点P到☉O 的切线长。
在纸上画出如图的图形，沿着直线PO 将纸对折，由于直线PO经过圆心O，所以PO是圆的一条对称轴， 两半圆重合,PA与PB，∠APO与∠BPO 有什么关系 ？
我们可以发现PA=PB，∠APO=∠BPO
切线长定理 ： 过圆外一点所画的圆的两条切线 ，它们的切线长相等， 这一点和圆心的连线平分这两条切线的夹角 。
已知 ： 如图， PA 、PB为☉O 的两条切线，切点分别为A、B ，求证：PA=PB，∠APO=∠BPO
证明：连接OA和OB，∵ PA切☉O于点A ∴OA⊥PA同理可得OB ⊥PB∵OA=OB OP=OP∴Rt△OAP ≌ Rt△OBP ∴ PA=PB，∠APO=∠BPO
如图是一张三角形铁皮 ，如何在它上面截一个面积最大的圆形铁皮？
可能大家都会想到这样一个圆 ，它与三角形的三条边都相切 ， 那么这样的圆存在吗 ? 如果存在 ? 我们又如何把它画出来呢 ？
如图，在 △ABC 中，如果有一个圆与 AB、AC、BC都相切，那么该圆的圆心到这三边的距离都等于半径，如何找到这个圆心呢？
因为与 △ABC的边 AB、AC都相切的圆的圆心到边AB、AC的距离相等 ，所以圆心一定在 ∠BAC 的平分线上。同理 ，和边 AB、BC都相切的圆的圆心一定在 ∠ABC的平分线上 。 设这两条角平分线的交点为 I， 则该点到三边的距离都相等 。 因此以I为圆心 、点I到 AB的距离为半径作圆 ， ☉ I必与 △ABC的三条边都相切。因为点 I 是唯一的 ， 所以I也是唯一的 。
与三角形各边都相切的圆叫做这个三角形的内切圆 ，三角形的内切圆的圆心叫做这个三角形的内心 ，这个三角形叫做这个圆的 外切三角形 ，三角形的内心就是三角形三条角平分线的交点 。
一个三角形的内切圆是唯一的 。
如图：已知PA是⊙O的切线，A为切点, AB是⊙O 的直径 , BC//OP交⊙O于点C。求证：PC与⊙O 相切。
∴∠ OCB=∠OBC.
∴ ⊿POC ≌ ⊿POA(SAS)
∴∠ OCB=∠POC.
∠ OBC=∠POA.
∴∠POC=∠POA.
∵ OP=OP，OA=OB
∴∠ PCO=∠PAO.
∴∠ PCO= ∠ PAO= 900.
∴ PC是⊙O的切线.
∴ PC⊥半径ＯC于点C
∵ ⊙O 切AP于A,
已知：△ABC内接于☉O，过点A作直线EF.（1）如图1，AB为直径，要使EF为☉O的切线，还需添加的条件是（只需写出两种情况）： ① _________ ；② _____________ .（2）如图2，AB是非直径的弦，∠CAE=∠B，求证：EF是☉O的切线.
证明：连接AO并延长交☉O于D,连接CD,则AD为☉O的直径.∴ ∠D+∠DAC=90 °,∴ ∠D=∠B,又∵ ∠CAE=∠B,∴ ∠D=∠CAE,∴ ∠DAC+∠EAC=90°,∴EF是☉O的切线.
经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
过圆外一点所画的圆的两条切线 ，它们的切线长相等， 这一点和圆心的连线平分这两条切线的夹角 。
27.2.3 切线（1）定义法（2）数量关系法（3）判定定理