






- 27.2.2 直线与圆的位置关系 课件+教学设计 课件 3 次下载
- 27.2.3 切线 课件+教学设计 课件 4 次下载
- 27.4 正多边形和圆 课件+教学设计 课件 4 次下载
- 28.1.1 普查和抽样调查 课件+教学设计 课件 1 次下载
- 28.1.2 这样选择样本合适吗 课件+教学设计 课件 1 次下载
华师大版九年级下册27.3 圆中的计算问题优秀教学课件ppt
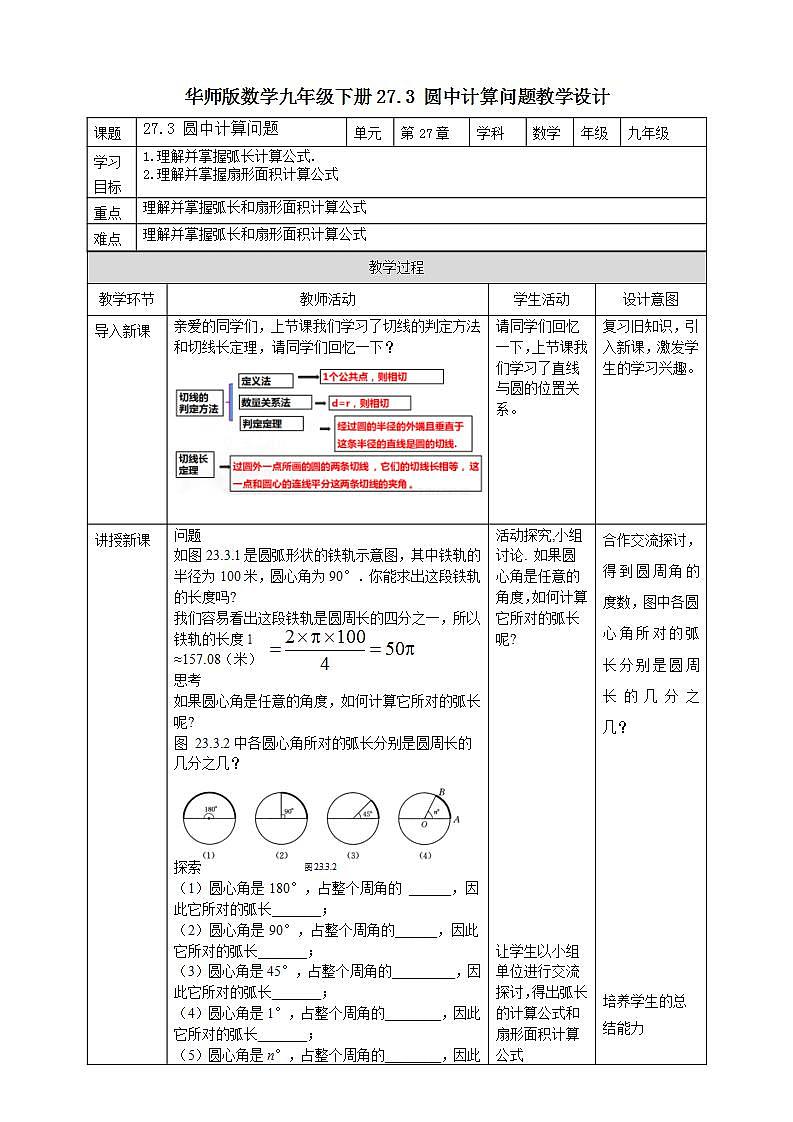
展开亲爱的同学们,上节课我们学习了切线的判定方法和切线长定理,请同学们回忆一下。
经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
过圆外一点所画的圆的两条切线 ,它们的切线长相等, 这一点和圆心的连线平分这两条切线的夹角 。
如图23.3.1是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗?
我们容易看出这段铁轨是圆周长的四分之一,所以铁轨的长度l≈157.08(米)
如果圆心角是任意的角度,如何计算它所对的弧长呢?
图 23.3.2中各圆心角所对的弧长分别是圆周长的几分之几?
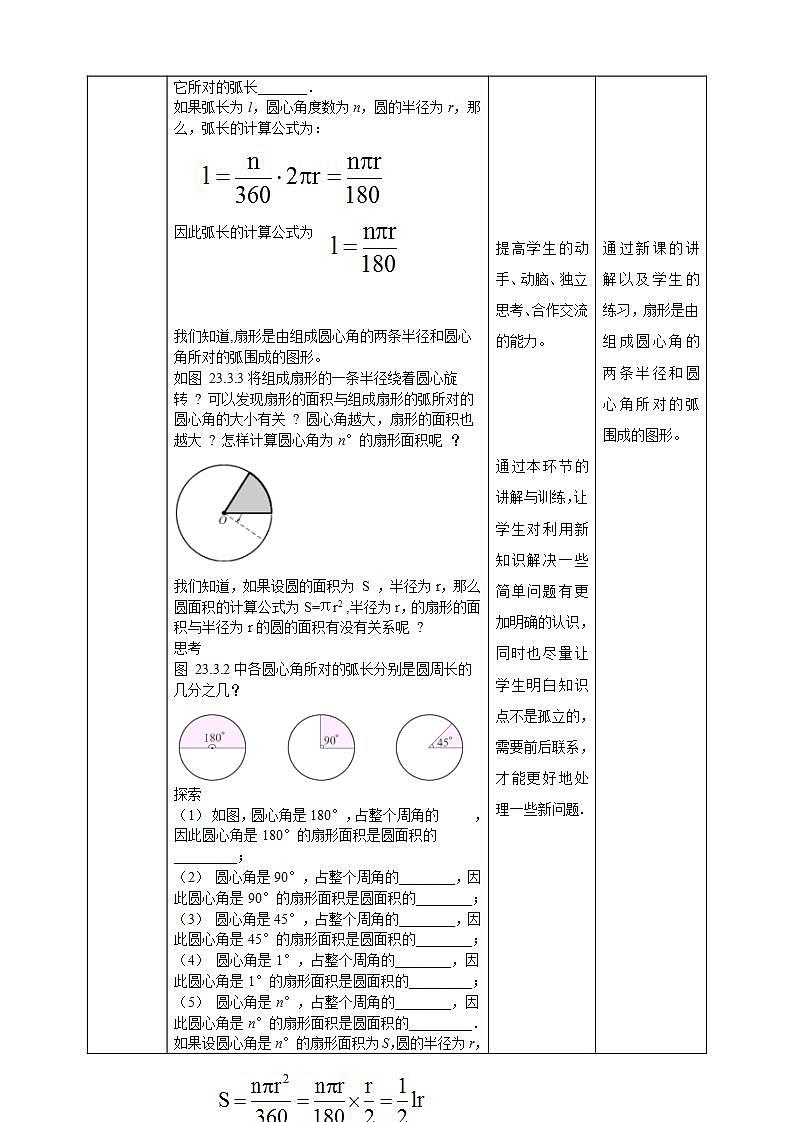
(1)圆心角是180°,占整个周角的 ______,因此它所对的弧长_______;(2)圆心角是90°,占整个周角的______,因此它所对的弧长_______;(3)圆心角是45°,占整个周角的_________,因此它所对的弧长_______;(4)圆心角是1°,占整个周角的________,因此它所对的弧长_______;(5)圆心角是n°,占整个周角的________,因此它所对的弧长_______.
(1)圆心角是180°,占整个周角的 ,因此它所对的弧长____________ ;(2)圆心角是90°,占整个周角的 ,因此它所对的弧长_________________________ ;(3)圆心角是45°,占整个周角的_________,因此它所对的弧长__________________________ ;
(4)圆心角是1°,占整个周角的__________,因此它所对的弧长_________________ ;(5)圆心角是n°,占整个周角的__________,因此它所对的弧长_____________________.
如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为:
我们知道,扇形是由组成圆心角的两条半径和圆心角所对的弧围成的图形。
如图 23.3.3将组成扇形的一条半径绕着圆心旋转 ? 可以发现扇形的面积与组成扇形的弧所对的圆心角的大小有关 ? 圆心角越大,扇形的面积也越大 ? 怎样计算圆心角为n°的扇形面积呢 ?
我们知道,如果设圆的面积为 S ,半径为r,那么圆面积的计算公式为S=πr2 ,半径为r,的扇形的面积与半径为r的圆的面积有没有关系呢 ?
(1) 如图,圆心角是180°,占整个周角的 ,因此圆心角是180°的扇形面积是圆面积的_________;(2) 圆心角是90°,占整个周角的________,因此圆心角是90°的扇形面积是圆面积的________; (3) 圆心角是45°,占整个周角的________,因此圆心角是45°的扇形面积是圆面积的________;
(4) 圆心角是1°,占整个周角的________,因此圆心角是1°的扇形面积是圆面积的_________; (5) 圆心角是n°,占整个周角的________,因此圆心角是n°的扇形面积是圆面积的_________.
如果设圆心角是n°的扇形面积为S,圆的半径为r,那么扇形的面积为:
因此扇形面积的计算公式为
例1 如图,圆心角为60°的扇形的半径为10厘米,求这个扇形的面积和周长(π≈3.14).
52.36(平方厘米);
30.47(厘米)
解:因为n=60°,r=10厘米,所以扇形面积为
(母线有无数条,母线都是相等的 )
我们把圆锥底面圆周上任意一点与圆锥顶点的连线叫做圆锥的母线 。连结顶点与底面圆心的线段叫做圆锥的高 。
我们知道圆锥是由一个底面和一个侧面围成的,如图23.3.6
如图23.3.7,沿着圆锥的母线,把圆锥的侧面展开 ,得到一个扇形 , 这个扇形的弧长等于圆锥底面的周长 , 而扇形的半径等于圆锥的母线的长 。
圆锥的侧面展开图是一个扇形 。
想一想:底面半径为r,高为h 的圆柱的侧面展开图是什么形状 ?
例2 一个圆锥的侧面展开图是一个圆心角为120°、 弧长为20π的扇形 ,试求该圆锥底面的半径及它的母线的长 。
解:设该圆锥底面的半径为 r母线的长为 a 则 2πr=20π可得 r=10又 可得 a=30
1 .圆锥的底面半径为3cm,母线长为6cm,则这个圆锥侧面展开图扇形的圆心角是_______。3 .一个扇形的半径为30cm,圆心角为120度,用它做成一个圆锥的侧面,那么这个圆锥的底面半径为_____ 。
如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一 点,PA=PC,∠C=30°.(1)求证:CP是⊙O的切线;(2)若⊙O的直径为8,求阴影部分的面积。
(1)证明:连接OP,如解图所示,∵PA=PC,∠C=30°,∴∠A=∠C=30°,∴∠APC=120°,∵OA=OP,∴∠OPA=∠A=30°,∴∠OPC=120°-30°=90°,即OP⊥CP,∴CP是⊙O的切线;
(2)解:∵AB是⊙O的直径,∴∠APB=90°,∴∠OBP=90°-∠A=60°,∵OP=OB=4,∴△OBP是等边三角形,∴∠POC=60°,∴OC=2OP=2OB=8,
27. 3 圆中计算问题(1)弧长(2)扇形面积(3)圆锥
初中数学华师大版九年级下册27.3 圆中的计算问题评优课课件ppt: 这是一份初中数学华师大版九年级下册27.3 圆中的计算问题评优课课件ppt,共17页。PPT课件主要包含了复习回顾,弧长的计算公式,生活中的圆锥,探究新知,圆锥有几条母线,底面半径r,a2h2+r2,πr20π,可得r10,可得a30等内容,欢迎下载使用。
数学九年级下册第27章 圆27.3 圆中的计算问题优秀ppt课件: 这是一份数学九年级下册第27章 圆27.3 圆中的计算问题优秀ppt课件,共22页。PPT课件主要包含了复习回顾,C2πr,Sπr2,探究新知,扇形的周长为,随堂练习,∶36等内容,欢迎下载使用。
初中数学华师大版九年级下册27.3 圆中的计算问题优质课件ppt: 这是一份初中数学华师大版九年级下册27.3 圆中的计算问题优质课件ppt,文件包含273圆中的计算问题2课件pptx、273圆中的计算问题2教案docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。













