



- 27.2.3 切线 课件+教学设计 课件 4 次下载
- 27.3 圆中计算问题 课件+教学设计 课件 4 次下载
- 28.1.1 普查和抽样调查 课件+教学设计 课件 1 次下载
- 28.1.2 这样选择样本合适吗 课件+教学设计 课件 1 次下载
- 28.2.1简单的随机抽样 课件+教学设计 课件 4 次下载
初中数学华师大版九年级下册27.4 正多边形和圆完美版教学课件ppt
展开亲爱的同学们,之前我们已经学过正多边形,请同学们回忆一下什么是正多边形?正多边形都是轴对称图形吗?
各条边相等, 各个角也相等的多边形是正多边形,等边三角形是正三角形,正方形是正四边形 ,正多边形都是轴对称图形 。
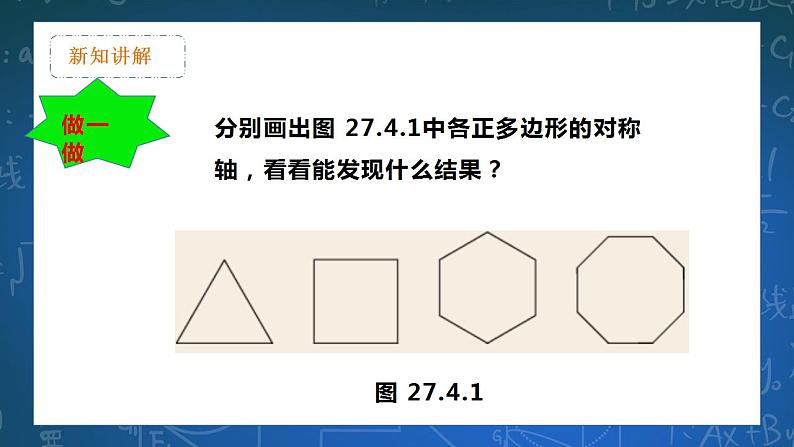
分别画出图 27.4.1中各正多边形的对称轴,看看能发现什么结果?
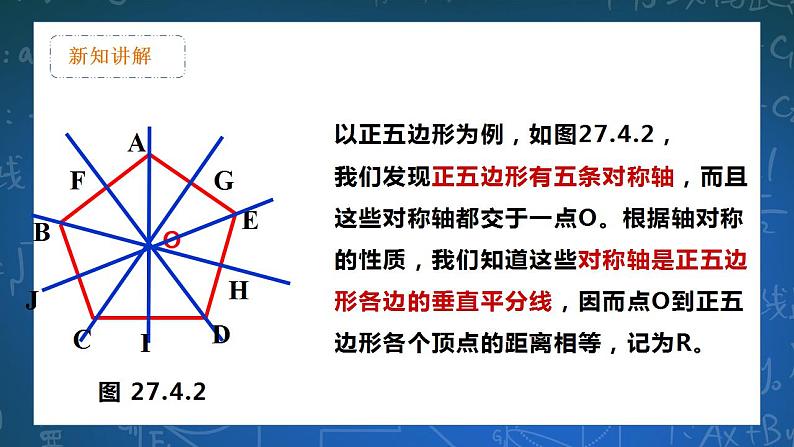
以正五边形为例,如图27.4.2,我们发现正五边形有五条对称轴,而且这些对称轴都交于一点O。根据轴对称的性质,我们知道这些对称轴是正五边形各边的垂直平分线,因而点O到正五边形各个顶点的距离相等,记为R。
那么以点O为圆心,R为半径的圆就过正五边形的各个顶点,它是该正五边形的外接圆。另外,这些对称轴也是正五边形各内角的平分线,根据角平分线的性质,点O到各边距离都相等,记为r,那么以点O为圆心,r为半径的圆就与正五边形的各条边都相切,它是正五边形的内切圆。(图27.4.3)
由此我们得到 ,任何正多边形都有一个外接圆和一个内切圆。
这两个圆有公共的圆心,称其为正多边形的中心 ,外接圆的半径叫做正多边形的半径, 内切圆的半径叫做正多边形的边心距 ,正多边形每一条边所对的外接圆的圆心角都相等,叫做正多边形的中心角 。
在同一个圆中,等弧对等弦 ,因此AB=BC=CD=DE=EA, 而根据圆周角定理 ,有∠A= ∠B = ∠C = ∠D = ∠E, 因此五边形ABCDE是正五边形。
这样我们就得到下面圆和正多边形的关系:把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形。
例:利用尺规作图,作出已知圆的内接正方形和内接正六边形。
解:内接正方形的作法:(1)用直尺任作圆的一条直径AC;(2)作与直径AC垂直的直径 BD;(3)顺次连结所得的圆上四点 ,则四边形 ABCD即为所求作的正方形 ,如图27.4.7
内接正六边形的作法 :(1)用直尺任作圆的一条直径 AD; (2) 以点 A为圆心 、OA 为半径作圆,与⊙O交于点 B、F;
(3)以点 D 为圆心 、OD为半径作圆 , 与⊙O交于点C、E;(4) 顺次连结所得的圆上六点 ,则六边形 ABCDEF即为所求作的正六边形,如图 27.4.8。
如图 27.4.9从圆上某一点开始,依次以圆的半径长为半径作圆, 也可作出圆的内接正六边形 。
想一想 ,为什么这两种方法作出来的图形都是正六边形?
正六边形两条对边之间的距离是2,则它的边长是( ) A B C D
解:如图所示,BF=2,过点A作AG⊥BF于G,则FG=1
又∵∠FAG=60°
如图,大的半圆的弧长为a,n个小圆的半径相等,且互相外切,其直径和等于大半圆的直径,若n个小半圆的总弧长为b,则a与b之间的关系是( )A B C D
即 ,故选A。
解:设大半圆的半径为R,小半圆的半径为r 由题意,得:
∴每个小半圆的弧长为
∴n个小半圆的总弧长
27. 4 正多边形和圆(1)外接圆(2)内切圆(3)尺规作图
华师大版九年级下册27.4 正多边形和圆完整版ppt课件: 这是一份华师大版九年级下册27.4 正多边形和圆完整版ppt课件,文件包含274正多边形和圆课件pptx、274正多边形和圆教案docx等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
数学九年级下册27.4 正多边形和圆一等奖ppt课件: 这是一份数学九年级下册27.4 正多边形和圆一等奖ppt课件,文件包含274正多边形和圆pptx、第27章圆274正多边形和圆docx、274正多边形和圆同步练习docx等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
初中数学27.4 正多边形和圆授课ppt课件: 这是一份初中数学27.4 正多边形和圆授课ppt课件,共23页。PPT课件主要包含了图片引入,正多边形,各边相等,各角相等,缺一不可,观察与思考,想一想,知识要点,完成下面的表格,练一练等内容,欢迎下载使用。