








利用函数性质判定方程解的存在性PPT课件免费下载
展开§1 方程解的存在性及方程的近似解
1.1 利用函数性质判定方程解的存在性
一、【素养目标】
1.结合学过的函数图象,了解函数的零点与方程解的关系.2.结合具体连续函数及其图象的特点,了解函数零点存在定理.
二、【课程的主要内容】
1.理解函数的零点、方程的根与图象与x轴交点三者之间的关系.(数学抽象)2.会借助零点存在定理判断函数的零点所在的大致区间.(直观想象)3.能借助函数单调性及图象判断零点个数.(逻辑推理)
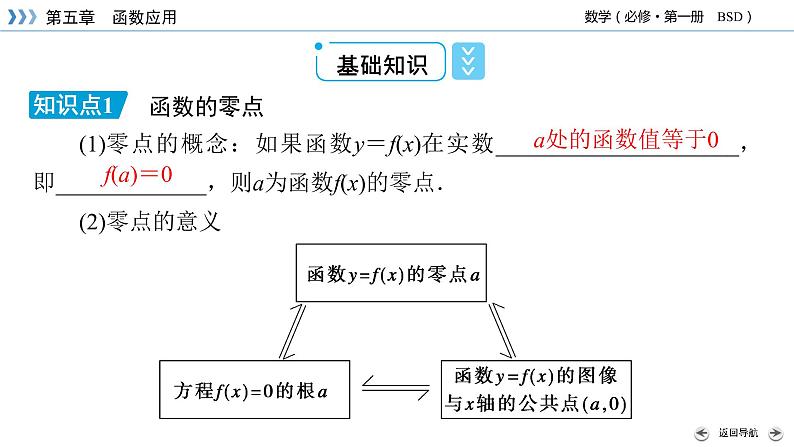
函数的零点(1)零点的概念:如果函数y=f(x)在实数_____________________,即_____________,则a为函数f(x)的零点.(2)零点的意义
思考1:(1)函数的零点是点吗?(2)所有的函数都有零点吗?
零点存在定理(1)零点存在定理:若函数y=f(x)在闭区间[a,b]上的图象是一条_______的曲线,并且在区间端点的函数值_________,即___________ ,则在开区间(a,b)内,函数y=f(x)至少有一个零点,即在区间(a,b)内相应的方程_____________至少有一个解.(2)本质:函数在区间(a,b)内存在零点即方程f(x)=0有解的理论依据.(3)应用:判断函数零点(方程的解)所在区间或求规定区间内函数零点(方程的解)的个数等问题.
f(a)·f(b)<0
思考2:函数零点存在定理要求具备哪些条件?提示:定理要求具备两个条件:①函数在区间[a,b]上的图象是连续不断的一条曲线;②f(a)·f(b)<0.
三、【例题剖析】
1.函数y=x2-2x的零点是( )A.0,2B.-2,0 C.1,0D.-1,0[解析] 函数y=x2-2x的零点就是方程x2-2x=0的实数根,解x2-2x=0,得x1=0,x2=2.故选A.
2.下列各图象表示的函数中没有零点的是( )
[解析] 选项D中,函数图象与x轴没有交点,故该函数没有零点.
3.若函数f(x)=x2+ax+b的零点是2和-4,则a=_____,b=_______.
4.求函数y=(ax-1)(x+2)的零点.
求下列函数的零点:(1)y=x-1;(2)y=x2-x-6.[分析] 把每一个函数解析式因式分解,化为几个因式之积的形式,最好为一次因式,然后令每一个因式等于零再解.
解析:(1)令x-1=0,得x=1,∴函数y=x-1的零点是1.(2)y=x2-x-6=(x-3)(x+2),令(x-3)(x+2)=0,得x=-2或x=3,∴函数y=x2-x-6的零点是-2和3.
[归纳提升] 函数零点的求法:(1)代数法:求方程f(x)=0的实数根.(2)几何法:对于不能用求根公式的方程f(x)=0,可以将它与函数y=f(x)的图象联系起来,图象与x轴的交点横坐标即为函数的零点.
(2)令x2+2x+4=0,由于Δ=22-4×4=-12<0,所以方程x2+2x+4=0无解,所以函数f(x)=x2+2x+4不存在零点.(3)令2x-3=0,所以2x=3,解得x=lg23,所以函数f(x)=2x-3的零点是lg23.(4)令1-lg3x=0,所以lg3x=1,解得x=3,所以函数f(x)=1-lg3x的零点是3.
[解析] (1)由f(x)=0,即x2-7x+12=0得Δ=49-4×12=1>0,∴方程x2-7x+12=0有两个不相等的实数根3,4,∴函数f(x)有两个零点,分别是3,4.
[归纳提升] 判断函数零点个数的方法(1)解方程法:转化为解方程f(x)=0,方程有几个根,函数就有几个零点.(2)图象交点法:画出函数y=h(x)与y=g(x)的图象,根据图象的交点个数判断方程h(x)=g(x)有几个根,或函数y=h(x)-g(x)有几个零点.
[归纳提升] 判断函数零点所在区间的步骤(1)代入:将区间端点值代入函数求出函数的值.(2)判断:把所得的函数值相乘,并进行符号判断.(3)结论:若符号为正且函数在该区间内是单调函数,则在该区间内无零点,若符号为负且函数连续,则在该区间内至少有一个零点.
四、【课堂练习】
【对点练习】❸ 根据表格中的数据,可以断定方程ex-(x+2)=0(e≈2.72)的一个根所在的区间是( )A.(-1,0)B.(0,1)C.(1,2)D.(2,3)[解析] 令f(x)=ex-(x+2),则f(-1)=0.37-1<0,f(0)=1-2<0,f(1)=2.72-3<0,f(2)=7.40-4=3.40>0.由于f(1)·f(2)<0,所以方程ex-(x+2)=0的一个根在(1,2)内.
已知a是实数,函数f(x)=2|x-1|+x-a,若函数y=f(x)有且仅有两个零点,则实数a的取值范围是_____________.[分析] 把函数f(x)的两个零点问题转化为函数y=2|x-1|+x与y=a的图象有且仅有两个交点问题,画出两个函数的图象,然后利用数形结合思想求出参数a的范围.
[解析] 函数f(x)=2|x-1|+x-a有且仅有两个零点,即函数y=2|x-1|+x与y=a有且仅有两个交点.分别作出函数y=2|x-1|+x与y=a的图象,如图所示.由图易知,当a>1时,两函数的图象有且仅有两个不同的交点,故实数a的取值范围是(1,+∞).
[归纳提升] 已知函数有零点(方程有根)求参数的方法1.直接法:根据题设条件构建关于参数的不等式(组),通过解不等式(组)确定参数的取值范围.2.数形结合法:先对f(x)的解析式变形,将f(x)=0转化为h(x)=g(x)(h(x),g(x)的图象易画出),在同一平面直角坐标系中画出函数h(x),g(x)的图象,然后利用数形结合思想求解.
1.函数f(x)=x2+x+3的零点的个数是( )A.0B.1C.2D.3解析:令x2+x+3=0,Δ=1-12=-11<0,∴方程无实数根,故函数f(x)=x2+x+3无零点.
3.若函数f(x)=2x2-ax+3有一个零点是1,则f(-1)=______.[解析] ∵函数f(x)=2x2-ax+3有一个零点为1,∴2-a+3=0,∴a=5.∴f(x)=2x2-5x+3,∴f(-1)=2×(-1)2-5×(-1)+3=10.
4.函数f(x)=x2+kx-2k2的顶点在直线x=2上,求f(x)的零点.
北师大版 (2019)必修 第一册1.1 利用函数性质判定方程解的存在性集体备课ppt课件: 这是一份北师大版 (2019)必修 第一册1.1 利用函数性质判定方程解的存在性集体备课ppt课件,共38页。
高中数学北师大版 (2019)必修 第一册1.1 利用函数性质判定方程解的存在性教学课件ppt: 这是一份高中数学北师大版 (2019)必修 第一册1.1 利用函数性质判定方程解的存在性教学课件ppt,共19页。PPT课件主要包含了抛物线,开口向上,不一定,课堂小结,谢谢大家等内容,欢迎下载使用。
北师大版 (2019)必修 第一册1.1 利用函数性质判定方程解的存在性精品课件ppt: 这是一份北师大版 (2019)必修 第一册1.1 利用函数性质判定方程解的存在性精品课件ppt,文件包含北师大版2019数学必修第一册511《利用函数性质判定方程解的存在性》课件pptx、北师大版2019数学必修第一册511《利用函数性质判定方程解的存在性》学案docx、北师大版2019数学必修第一册511《利用函数性质判定方程解的存在性》教案docx等3份课件配套教学资源,其中PPT共43页, 欢迎下载使用。













