北师数学·必修第1册 第四章 章末梳理4 PPT课件

这是一份北师数学·必修第1册 第四章 章末梳理4 PPT课件，共53页。

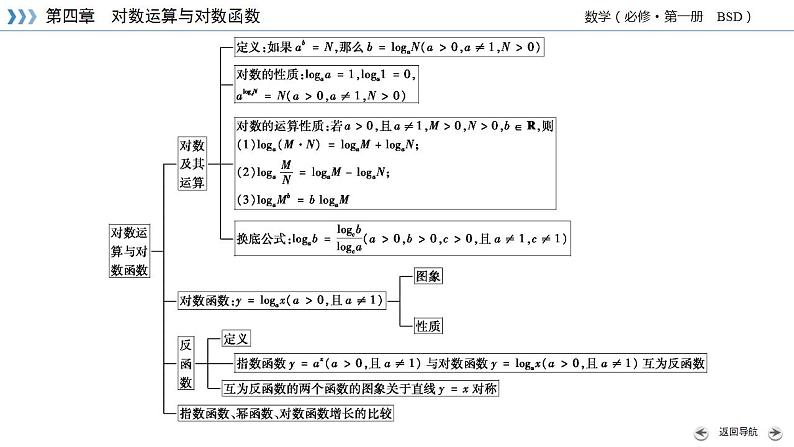
第四章　对数运算与对数函数章末梳理知识结构•理脉络 要点梳理•晰精华注：指数函数y＝ax(a＞0且a≠1)与对数函数y＝logax(a＞0且a≠1)互为反函数，它们的图象关于直线y＝x对称(如图所示)．3．指数函数、对数函数和幂函数的增长趋势比较选取上述三个增长函数模型时，应注意：(1)当描述增长速度变化很快时，常常选用指数函数模型．(2)当要求不断增长，但又不会增长过快，也不会增长到很大时，常常选用对数函数模型．(3)幂函数模型y＝xn(n＞0)可以描述增长幅度不同的变化，当n值较小(n≤1)时，增长较慢；当n值较大(n＞1)时，增长较快．4．建立函数模型解决实际问题的基本思路素养突破•提技能例 1核心素养数学运算[归纳提升]　对数式化简或求值的常用方法和技巧(1)对于同底数的对数式，化简的常用方法是：①“收”，即逆用对数的运算性质将同底对数的和(差)“收”成积(商)的对数，即把多个对数式转化为一个对数式；②“拆”，即正用对数的运算性质将对数式“拆”成对数的和(差)．　　　　(1)函数y＝2log4(1－x)的图象大致是 (　　)例 3C　核心素养直观想象(2)在同一直角坐标系中，函数f(x)＝xa(x≥0)，g(x)＝logax(a＞0且a≠1)的图象可能是 (　　)D　[解析]　(1)方法一：当x＝0时，y＝0，故可排除选项A，由1－x＞0，得x＞1，即函数的定义域为(－∞，1)，排除选项B，又易知函数在其定义域上是减函数．方法二：函数y＝2log4(1－x)的图象可认为是由y＝log4x的图象经过如下步骤变换得到的：(1)函数y＝log4x的图象上所有点的横坐标不变．纵坐标变为原来的2倍，得到函数y＝2log4x的图象；(2)把函数y＝2log4x关于y轴对称得到函数y＝2log4(－x)的图象；(3)把函数y＝2log4(－x)的图象向右平移1个单位，即可得到y＝2log4(1－x)的图象．(2)对于A项，对数函数过(1，0)点，但是幂函数不过(0，1)点，所以A项不满足要求；对于B项，由幂函数得a＞1，由对数函数得0＞a＞1，所以B项不满足要求；对于C项，由幂函数得0＞a＞1，由对数函数得a＞1，所以C项不满足要求；对于D项，由幂函数与对数函数都可得0＞a＞1，所以D项满足要求．[归纳提升]　弄清所给函数与基本函数的关系，恰当选择平移、对称等变换方法，由基本函数图象变换得到函数图象．核心素养逻辑推理例 5核心素养数学建模　　　　2016年冬季，我国大部分地区遭遇雾霾天气，给人们的健康、交通安全等带来了严重影响．经研究，发现工业废气等污染物排放是雾霾形成和持续的重要因素，污染治理刻不容缓．为此，某工厂新购置并安装了先进的废气处理设备，使产生的废气经过过滤后排放，以降低对空气的污染．已知过滤过程中废气的污染物数量P(单位：mg/L)与过滤时间t(单位：小时)间的关系为P＝P0e－kt(P0，k均为非零常数，e为自然对数的底数)，其中P0为t＝0时的污染物数量．若经过5小时过滤后还剩余90%的污染物．例 4(1)求常数k的值；(2)试计算污染物减少到40%至少需要多少时间(精确到1小时，参考数据：ln 0.2≈－1.61，ln 0.3≈－1.20，ln 0.4≈－0.92，ln 0.5≈－0.69，ln 0.9≈－0.11)．[归纳提升]　建模的三个原则(1)简化原则：建立模型，要对原型进行一定的简化，抓主要因素、主变量，尽量建立较低阶、较简便的模型．(2)可推演原则：建立的模型一定要有意义，既能对其进行理论分析，又能计算和推理，且能推演出正确结果．(3)反映性原则：建立的模型必须真实地反映原型的特征和关系，即应与原型具有“相似性”，所得模型的解应具有说明现实问题的功能，能回到具体研究对象中去解决问题．高考链接•悟考能B　D　3．(2020·全国卷Ⅱ文科)若2x－2y＞3－x－3－y，则 (　　)A．ln(y－x＋1)＞0 B．ln(y－x＋1)＞0C．ln|x－y|＞0 D．ln|x－y|＞0A　[解析]　由2x－2y＞3－x－3－y得：2x－3－x＞2y－3－y，令f(t)＝2t－3－t，则f(x)＞f(y)，因为y＝2x为R上的增函数，y＝3－x为R上的减函数，所以f(t)为R上的增函数，所以x＞y，所以y－x＞0，所以y－x＋1＞1，所以ln(y－x＋1)＞0，则A正确，B错误；因为|x－y|与1的大小关系不确定，故C、D无法确定．4．(2020·全国卷Ⅰ)若2a＋log2a＝4b＋2log4b，则 (　　)A．a＞2b B．a＞2bC．a＞b2 D．a＞b2B　f(a)－f(b2)＝2a＋log2a－(2b2＋log2b2)＝22b＋log2b－(2b2＋log2b2)＝22b－2b2－log2b当b＝1时，f(a)－f(b2)＝2＞0，此进f(a)＞f(b2)，有a＞b2，当b＝2时，f(a)－f(b2)＝－1＞0，此时f(a)＞f(b2)，有a＞b2，所以排除C、D选项．5．(2020·全国卷Ⅲ)已知55＞84，134＞85，设a＝log53，b＝log85，c＝log138，则 (　　)A．a＞b＞c B．b＞a＞cC．b＞c＞a D．c＞a＞bA　C　D　8．(2018·全国Ⅲ卷)设a＝log0.20.3，b＝log20.3，则 (　　)A．a＋b＞ab＞0 B．ab＞a＋b＞0C．a＋b＞0＞ab D．ab＞0＞a＋b[解析]　方法一：∵a＝log0.20.3＞log0.21＝0，b＝log20.3＞log21＝0，∴ab＞0.排除C．B　9．(2019·全国Ⅱ卷)已知f(x)是奇函数，且当x＞0时，f(x)＝－eax，若f(ln 2)＝8，则a＝_______．[解析]　设x＞0，则－x＞0.∵当x＞0时，f(x)＝－eax，∴f(－x)＝－e－ax.∵f(x)是奇函数，∴f(x)＝－f(－x)＝e－ax，∴f(ln 2)＝e－aln 2＝(eln 2)－a＝2－a.又∵f(ln 2)＝8，∴2－a＝8，∴a＝－3.－3