





初中数学北师大版八年级下册第六章 平行四边形3 三角形的中位线教学ppt课件
展开1. 理解三角形中位线的概念.2. 掌握三角形中位线定理的证明和有关应用.
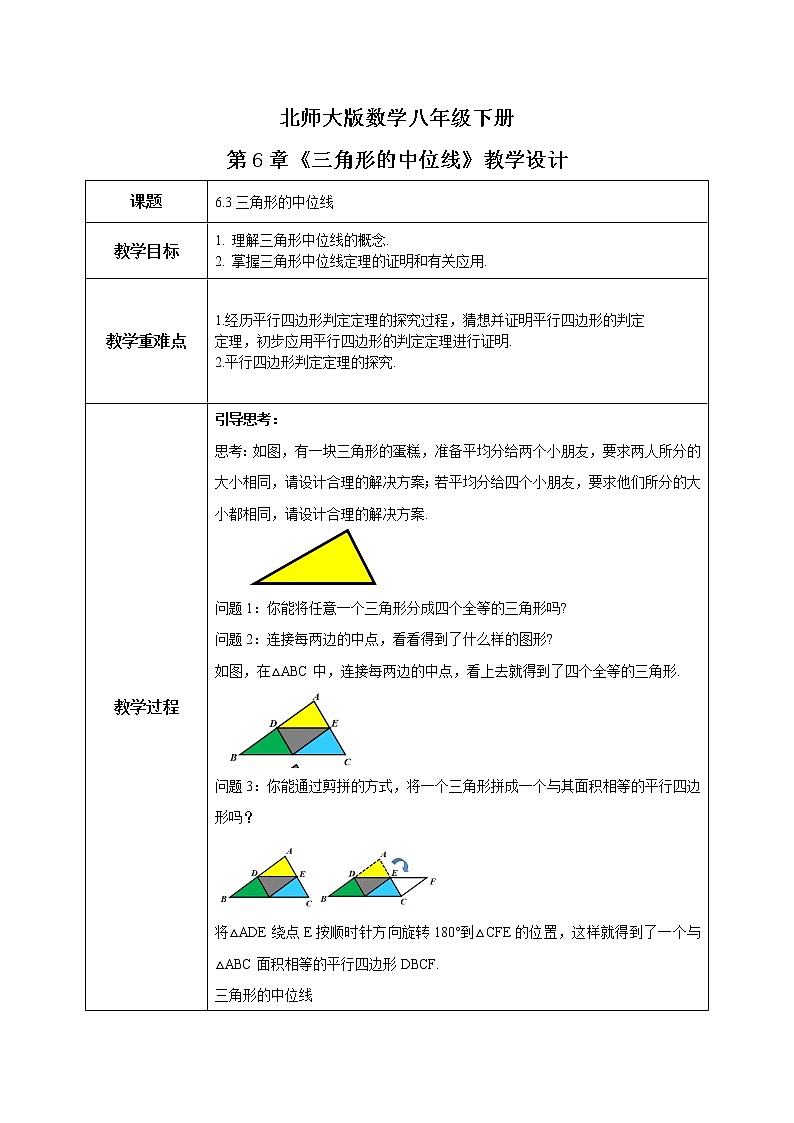
思考:如图,有一块三角形的蛋糕,准备平均分给两个小朋友,要求两人所分的大小相同,请设计合理的解决方案;若平均分给四个小朋友,要求他们所分的大小都相同,请设计合理的解决方案.
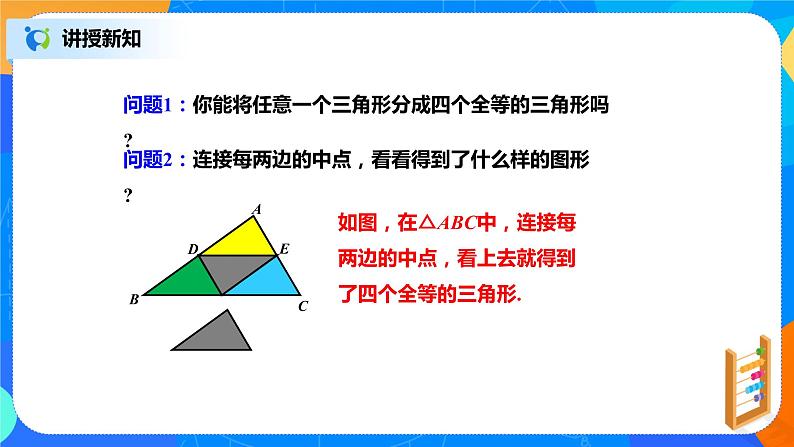
如图,在△ABC中,连接每两边的中点,看上去就得到了四个全等的三角形.
问题2:连接每两边的中点,看看得到了什么样的图形?
问题1:你能将任意一个三角形分成四个全等的三角形吗?
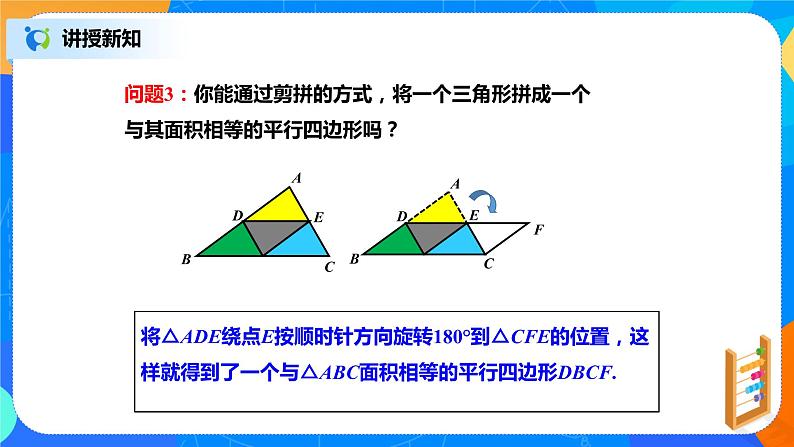
问题3:你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?
将△ADE绕点E按顺时针方向旋转180°到△CFE的位置,这样就得到了一个与△ABC面积相等的平行四边形DBCF.
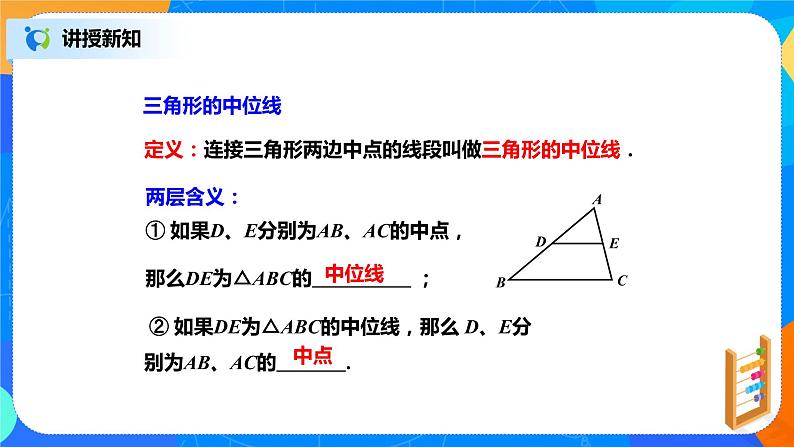
定义:连接三角形两边中点的线段叫做三角形的中位线.
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 .
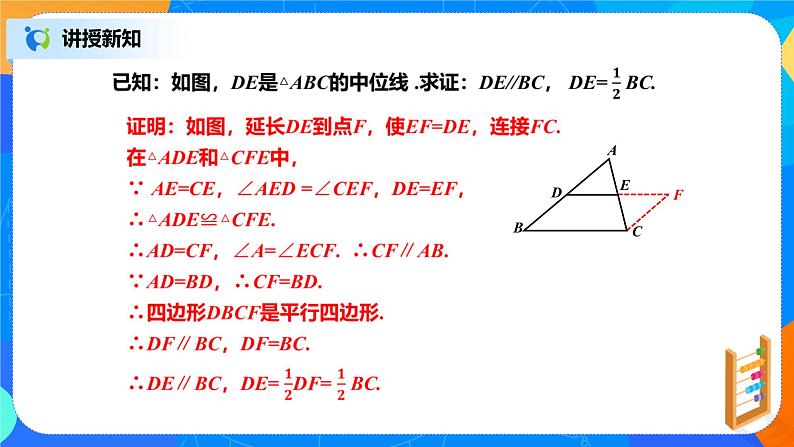
探究:如图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
探究:如图:在四边形ABCD中, E,F,G,H分别 为各边的中点. 求证:四边形EFGH是平行四边形.
提示:将四边形ABCD分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.
探究:如图:在四边形ABCD中, E,F,G,H分别为各边的中点. 求证:四边形EFGH是平行四边形.
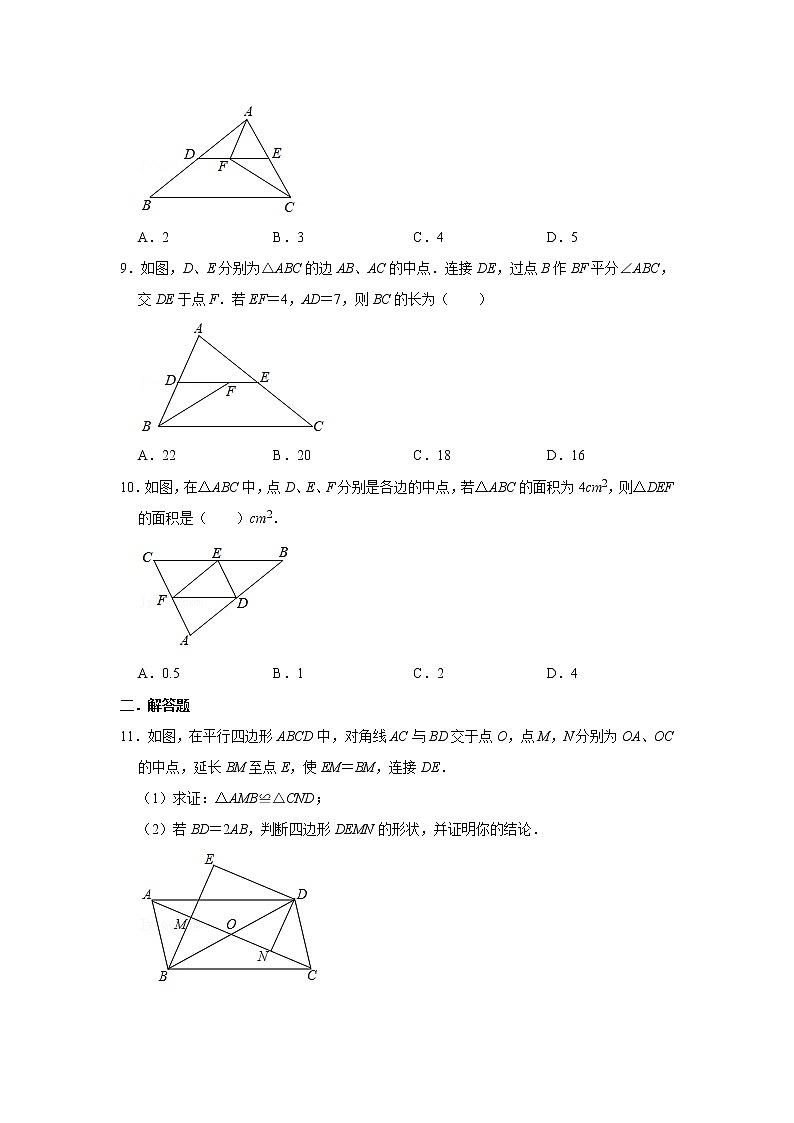
1. 如图,M是△ABC的边BC的中点,AN平分∠BAC, BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.(1) 求证:BN=DN;
证明:∵AN平分∠BAC,∴∠1=∠2.∵BN⊥AN,∴∠ANB=∠AND=90°.在△ABN和△ADN中,∠1=∠2,AN=AN,∠ANB=∠AND,∴△ABN≌△ADN.∴BN=DN.
解:∵△ABN≌△ADN,∴AD=AB=10.又∵点M是BC中点,∴MN是△BDC的中位线.∴CD=2MN=6.∴△ABC的周长 =AB+BC+CD+AD=10+15+6+10=41.
1. 如图,M是△ABC的边BC的中点,AN平分∠BAC, BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3.(2) 求△ABC的周长.
连接三角形两边中点的线段叫做三角形的中位线.
北师大版八年级下册4 多边形的内角与外角和优秀课件ppt: 这是一份北师大版八年级下册4 多边形的内角与外角和优秀课件ppt,文件包含2021年北师大版数学八年级下册《多边形的内角和与外角和》同步练习docx、《多边形的内角和与外角和》课件pptx、2021年北师大版数学八年级下册《多边形的内角和与外角和》教学设计docx等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
初中数学北师大版八年级下册2 平行四边形的判定多媒体教学课件ppt: 这是一份初中数学北师大版八年级下册2 平行四边形的判定多媒体教学课件ppt,文件包含《平行四边形的判定》课件pptx、2021年北师大版数学八年级下册《平行四边形的判定》同步练习docx、2021年北师大版数学八年级下册《平行四边形的判定》教学设计docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质图文课件ppt: 这是一份初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质图文课件ppt,文件包含《平行四边形的性质》课件pptx、2021年北师大版数学八年级下册《平行四边形的性质》同步练习docx、2021年北师大版数学八年级下册《平行四边形的性质》教学设计docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。














