








初中数学北师大版八年级下册2 平行四边形的判定多媒体教学课件ppt
展开1. 掌握平行四边形的第三条判定定理.2. 能综合运用平行四边形的判定方法和性质来解决问题.3. 通过实例认识“平行线之间的距离”.4. 探索并证明“夹在平行线之间的平行线段相等”.
取四根细木条,其中两根长度相等,另两根长度也相等,用图钉钉在一起,做成一个四边形,使等长的木条成为对边. 这个四边形是平行四边形吗?
猜想:两组对边分别相等的四边形是平行四边形.
已知:在四边形ABCD中,AB=CD,AD=CB,求证:四边形ABCD是平行四边形.
证明:如图,连接AC.在△ABC和△CDA中,∵AB=CD,AD=CB,AC=CA,∴ △ABC ≌ △CDA. ∴ ∠1=∠2,∠3=∠4.∴AB//CD,AD//CB.∴四边形ABCD是平行四边形(平行四边形的定义).
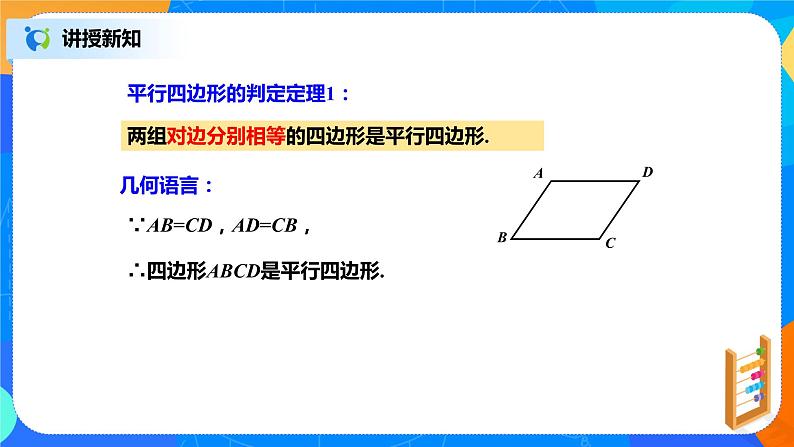
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
∵AB=CD,AD=CB,
∴四边形ABCD是平行四边形.
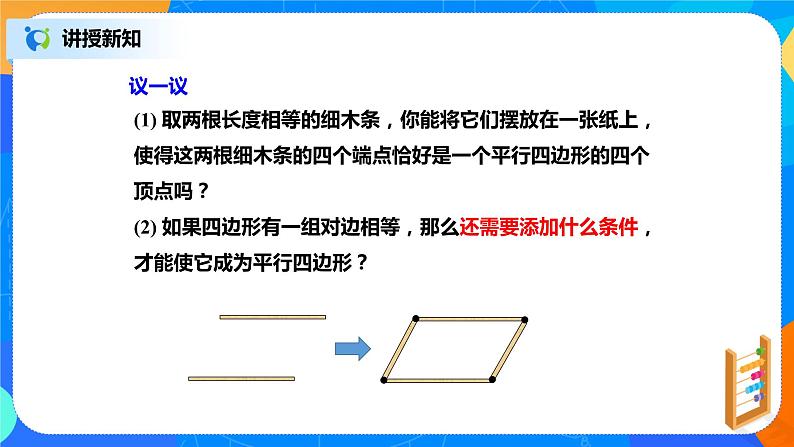
(1) 取两根长度相等的细木条,你能将它们摆放在一张纸上,使得这两根细木条的四个端点恰好是一个平行四边形的四个顶点吗?(2) 如果四边形有一组对边相等,那么还需要添加什么条件,才能使它成为平行四边形?
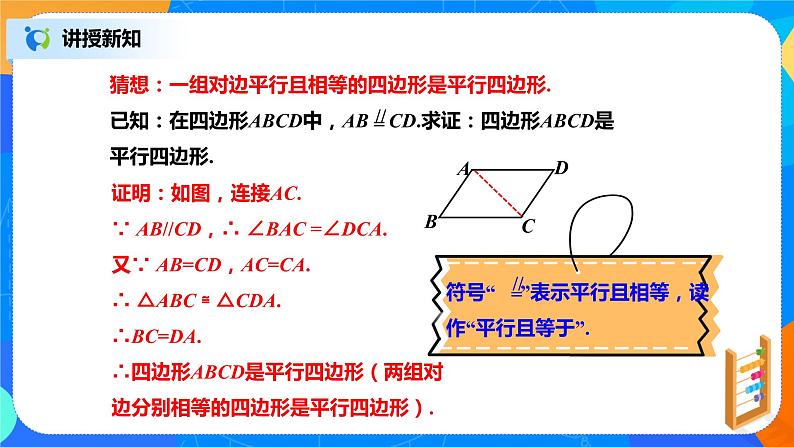
猜想:一组对边平行且相等的四边形是平行四边形.
已知:在四边形ABCD中,AB CD.求证:四边形ABCD是平行四边形.
证明:如图,连接AC.∵ AB//CD,∴ ∠BAC =∠DCA.又∵ AB=CD,AC=CA.∴ △ABC ≌ △CDA. ∴BC=DA.∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
例1 如图,在平行四边形ABCD中,E、F分别是边AD和CB的中点.求证:四边形BFDE是平行四边形.
工具:两根不同长度的细木条.动手:能否合理摆放这两根细木条,使得连接四个顶点后成为平行四边形?思考:你能说明你得到的四边形是平行四边形吗?
已知:如图,四边形ABCD的对角线AC、BD相交于点O,并且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
证明:∵OA=OC,OB=OD,∠AOB=∠COD,∴△AOB≌△COD.∴ AB=CD.同理可得:BC=AD.∴ 四边形ABCD是平行四边形.
猜想:对角线互相平分是四边形是平行四边形.
平行四边形判定定理3:
∵OA=OC,OB=OD,∴四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
例2 已知:如图,在平行四边形ABCD中,点E、F在对角线AC上,并且AE=CF.求证:四边形BFDE是平行四边形.
在笔直的铁轨上,夹在铁轨之间的平行枕木是否一样长?你能说明理由吗?
已知:如图,直线a∥b,A,B是直线a上任意两点,AC⊥b,BD⊥b,垂足分别为C,D.求证:AC=BD.
证明:∵AC⊥CD,BD⊥CD,∴∠1=∠2=90°.∴AC∥BD.∵ AB∥CD,∴四边形ACDB是平行四边形(平行四边形的定义).∴AC=BD(平行四边形的对边相等).
数学表达式:如图,A,C是l1上任意两点,∵l1∥l2,AB⊥l2,CD⊥l2,∴AB=CD.
从上例得到:如果两条直线互相平行,则其中一条直线上的任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离.
拓展:(1) 夹在两条平行线间的任何平行线段都相等; (2) 等底等高的三角形的面积相等.
例3 如图,在平行四边形ABCD中,点M,N分别是AD,BC上的两点,点E,F在对角线BD上,且DM=BN,BE=DF.求证:四边形MENF是平行四边形.
证明: ∵四边形ABCD是平行四边形, ∴AD∥BC.∴∠MDF=∠NBE.∵DM=BN,DF=BE,∴△MDF ≌△NBE.∴MF=NE,∠MFD=∠NEB.∴∠MFE=∠NEF.∴MF∥NE.∴四边形MENF是平行四边形.
证明:∵四边形ABCD是平行四边形,∴BO=DO,AO=CO,AB=CD,AB∥CD.∴∠ABD =∠CDB.∵AE⊥BD于E,CF⊥BD于F,∴∠AEB=∠CFD=90°.在△ABE和△CDF中,
1. 如图,在平行四边形ABCD中,对角线AC,BD相交于O点,AE⊥BD于E,CF⊥BD于F,BG⊥AG于G,DH⊥AC于H.求证:四边形GEHF是平行四边形.
2. 如图,在平行四边形ABCD中,点E在BC的延长线,且DE∥AC.请写出BE与BC的数量关系,并证明你的结论.
结论:BE=2BC.证明:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC,即AD∥CE.∵DE∥AC,∴四边形ADEC为平行四边形.∴AD=CE.∴CE=BC.∴BE=2BC.
平行四边形的判定从边来判定1. 两组对边分别平行的四边形是平行四边形 2. 两组对边分别相等的四边形是平行四边形3. 一组对边平行且相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形
1. 平行线间的距离:两条平行线中,一条直线上任一点到另一条直线的距离,叫做这两条平行线之间的距离;
2. 平行线间的距离的性质:如果两条直线平行,则其中一条直线上任意两点到另一条直线的距离相等. 即:平行线间的距离处处相等.
北师大版八年级下册4 多边形的内角与外角和优秀课件ppt: 这是一份北师大版八年级下册4 多边形的内角与外角和优秀课件ppt,文件包含2021年北师大版数学八年级下册《多边形的内角和与外角和》同步练习docx、《多边形的内角和与外角和》课件pptx、2021年北师大版数学八年级下册《多边形的内角和与外角和》教学设计docx等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
初中数学北师大版八年级下册第六章 平行四边形3 三角形的中位线教学ppt课件: 这是一份初中数学北师大版八年级下册第六章 平行四边形3 三角形的中位线教学ppt课件,文件包含2021年北师大版数学八年级下册《三角形的中位线》同步练习docx、《三角形的中位线》课件pptx、2021年北师大版数学八年级下册《三角形的中位线》教学设计docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质图文课件ppt: 这是一份初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质图文课件ppt,文件包含《平行四边形的性质》课件pptx、2021年北师大版数学八年级下册《平行四边形的性质》同步练习docx、2021年北师大版数学八年级下册《平行四边形的性质》教学设计docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。














