北师大版八年级下册第一章 三角形的证明1 等腰三角形习题ppt课件

这是一份北师大版八年级下册第一章 三角形的证明1 等腰三角形习题ppt课件，共31页。PPT课件主要包含了习题链接，2ED⊥DF等内容，欢迎下载使用。
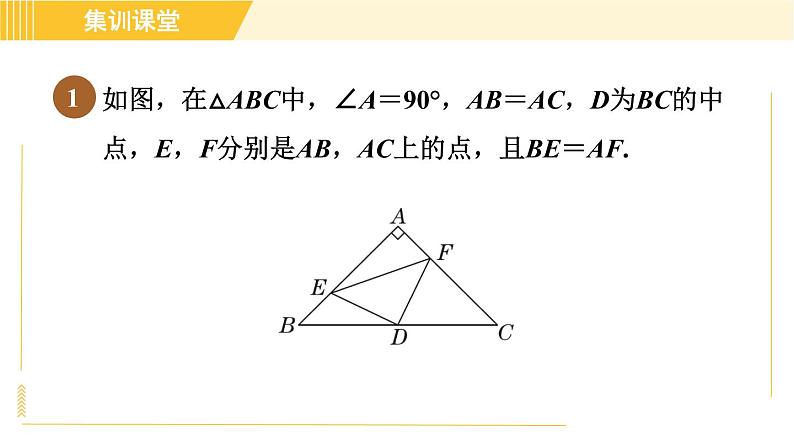
如图，在△ABC中，∠A＝90°，AB＝AC，D为BC的中点，E，F分别是AB，AC上的点，且BE＝AF.
求证：(1)ED＝DF；
证明：连接AD.∵AB＝AC，D为BC的中点，∴AD⊥BC，∠BAD＝∠CAD，∠B＝∠C.∵∠BAC＝90°，∴∠B＝∠C＝∠BAD＝∠CAD＝45°.∴AD＝BD.
证明：∵△BED≌△AFD，∴∠BDE＝∠ADF.∴∠BDE＋∠EDA＝∠EDA＋∠ADF＝90°.∴∠EDF＝90°.∴ED⊥DF.
如图，在△ABC中，AC＝2AB，AD平分∠BAC交BC于D，E是AD上一点，且EA＝EC.求证：EB⊥AB.
证明：如图，作EF⊥AC于点F.∵EA＝EC，∴AF＝FC.∴AC＝2AF.又∵AC＝2AB，∴AF＝AB.∵AD平分∠BAC，∴∠BAE＝∠FAE.又∵AE＝AE，∴△ABE≌△AFE(SAS)．∴∠ABE＝∠AFE＝90°.∴EB⊥AB.
如图，BD平分∠ABC交AC于D，点E为CD上一点，且AD＝DE，EF∥BC交BD于点F.求证：AB＝EF.
∵AG∥EF，BC∥EF，∴AG∥BC.∴∠G＝∠CBD.∵BD平分∠ABC，∴∠ABG＝∠CBG.∴∠ABG＝∠G.∴AB＝AG.∴AB＝EF.
如图，点E在△ABC的AC边的延长线上，点D在AB边上，DE交BC于点F，DF＝EF，BD＝CE.求证：△ABC是等腰三角形．
又∵BD＝CE，∴BD＝DG.∴∠DBG＝∠DGB.∵DG∥AC，∴∠DGB＝∠ACB.∴∠B＝∠ACB.∴AB＝AC，即△ABC是等腰三角形．
如图，在△ABC中，AB＝AC，点P从点B出发沿线段BA移动(点P与A，B不重合)，同时，点Q从点C出发沿线段AC的延长线移动，点P，Q移动的速度相同，PQ与直线BC相交于点D.
(1)求证：PD＝QD.
证明：如图，过点P作PF∥AC交BC于点F.∵点P和点Q同时出发，且速度相同，∴BP＝CQ.∵PF∥AQ，∴∠PFB＝∠ACB，∠DPF＝∠CQD.∵AB＝AC，∴∠B＝∠ACB.∴∠B＝∠PFB.∴BP＝PF.∴PF＝QC.
(2)过点P作直线BC的垂线，垂足为E.P，Q在移动的过程中，线段BE，DE，CD中是否存在长度保持不变的线段？请说明理由．
如图，在等边三角形ABC中，D是边AC延长线上一点，延长BC至点E，使CE＝AD，DG⊥BE于点G.求证：BG＝EG.
证明：如图，过点D作DF∥BE，交AB的延长线于F.∵△ABC是等边三角形，∴AB＝AC＝BC，∠ABC＝∠ACB＝∠AFD＝∠ADF＝∠A＝60°.∴△ADF是等边三角形．∴AD＝DF＝AF.∴CD＝BF.
如图，AB∥CD，∠1＝∠2，AD＝AB＋CD.(1)求证：BE＝CE；
证明：如图，延长AB，DE交于点F.∵AB∥CD，∴∠F＝∠2.∵∠1＝∠2，∴∠1＝∠F.∴AD＝AF.∵AD＝AB＋CD，∴DC＝BF.又∵∠DEC＝∠FEB，∴△DCE≌△FBE(AAS)．∴BE＝CE.
(2)求证：AE⊥DE；
证明：由(1)知△DCE≌△FBE，AD＝AF，∴DE＝EF.∴AE⊥DE.
(3)求证：AE平分∠DAB.
∵DE＝EF，AD＝AF，∴AE平分∠DAB.
如图，在△ABC中，AD为中线，点E为AB上一点，AD，CE交于点F，且AE＝EF.求证：AB＝CF.
证明：如图，延长AD至点G，使DG＝AD，连接CG.∵BD＝CD，∠ADB＝∠GDC，∴△ABD≌△GCD(SAS)．∴AB＝CG，∠G＝∠EAF.∵AE＝EF，∴∠EAF＝∠EFA.又∵∠EFA＝∠CFG，∴∠G＝∠GFC.∴CG＝CF.∴AB＝CF.
如图，在△ABC中，∠BAC＝2∠B，CD平分∠ACB交AB于点D.求证：AC＋AD＝BC.
证法一：如图①，延长CA至点E，使EA＝AD，连接ED，则∠E＝∠ADE.∴∠BAC＝∠E＋∠ADE＝2∠E.∵∠BAC＝2∠B，∴∠E＝∠B.又∵∠ECD＝∠BCD，CD＝CD，∴△CDE≌△CDB(AAS)．∴CE＝CB.∵CE＝AC＋AE＝AC＋AD，∴AC＋AD＝BC.
证法二：如图②，延长DA到点E，使AE＝AC，连接CE，则∠E＝∠ACE.∴∠BAC＝∠E＋∠ACE＝2∠E.∵∠BAC＝2∠B，∴∠B＝∠E＝∠ACE.∴BC＝EC.∵∠ACD＝∠BCD，∴∠ADC＝∠B＋∠BCD＝∠B＋∠ACD.又∵∠DCE＝∠ACE＋∠ACD＝∠B＋∠ACD，∴∠ADC＝∠DCE.∴DE＝CE.∴DE＝BC.∴AC＋AD＝AE＋AD＝DE＝BC.
【2021·南京鼓楼模拟】如图，已知在△ABC中，AB＝AC，∠A＝100°，BE平分∠ABC交AC于点E.(1)求证：BC＝BE＋AE.
证明：在BC上截取BD＝BE，连接DE，如图所示．∵AB＝AC，∠BAC＝100°，∴∠ABC＝∠C＝(180°－100°)÷2＝40°.∵BE平分∠ABC，∴∠CBE＝∠ABE＝20°.∵BD＝BE，∴∠BDE＝∠BED＝(180°－20°)÷2＝80°.又∵∠BDE＝∠C＋∠CED，∠C＝40°，∴∠CED＝40°＝∠C.∴DE＝DC.
过点E作EM⊥BA交BA的延长线于点M，EN⊥BC于点N.∵BE平分∠ABC，EM⊥BA，EN⊥BC，∴EM＝EN.∵∠BAC＝100°，∴∠CAM＝180°－100°＝80°.
(2)探究：若∠A＝108°，则BC的长等于哪两条线段的和呢？试说明理由．
解：BC＝CE＋AB.理由如下：在CB上截取CP＝CE，连接PE，如图所示．∵AB＝AC，∠A＝108°，∴∠ABC＝∠C＝(180°－108°)÷2＝36°.∵CP＝CE，∴∠CPE＝(180°－36°)÷2＝72°.∴∠BPE＝180°－72°＝108°.∴∠BPE＝∠A.