2020-2021学年18.2.3 正方形习题课件ppt

这是一份2020-2021学年18.2.3 正方形习题课件ppt，共26页。PPT课件主要包含了答案显示，见习题，平行四边形，AB＝AD，答案不唯一等内容，欢迎下载使用。

AB＝AD(答案不唯一)
1．正方形是轴对称图形，它有______条对称轴．若正方形的边长为a，则它的对角线长为________，面积为________．
2．【2021·新疆】下列图形中，不是轴对称图形的是(　　)
3．如图是以正方形的边长为直径，在正方形内画半圆得到的图形，则此图形的对称轴有(　　)A．2条 　　B．4条C．6条 　　D．8条
4．判定一个四边形是正方形，就要判定它既是______，又是________．具体判定方法如下：对角线互相垂直的________是正方形；对角线相等的________是正方形；对角线互相垂直且相等的____________是正方形；有一个角是直角的________是正方形；有一组邻边相等的________是正方形．
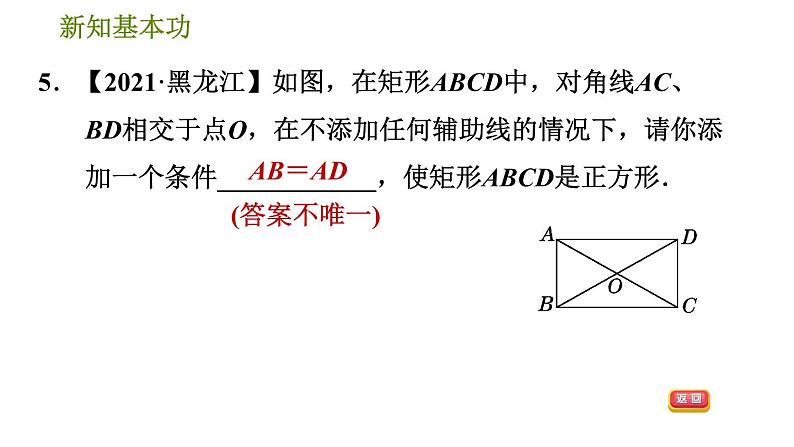
5．【2021·黑龙江】如图，在矩形ABCD中，对角线AC、BD相交于点O，在不添加任何辅助线的情况下，请你添加一个条件____________，使矩形ABCD是正方形．
6．【2020·台州】下面是关于某个四边形的三个结论：①它的对角线相等；②它是一个正方形；③它是一个矩形．下列推理过程正确的是(　　)A．由②推出③，由③推出①B．由①推出②，由②推出③C．由③推出①，由①推出②D．由①推出③，由③推出②
7．【2021·玉林】如图，一个四边形顺次添加下列条件中的三个条件便得到正方形：a．两组对边分别相等b．一组对边平行且相等c．一组邻边相等　d．一个角是直角顺次添加的条件：①a→c→d　②b→d→c③a→b→c　则正确的是(　　)A．① B．③ C．①② D．②③
8．【2020·襄阳】已知四边形ABCD是平行四边形，AC，BD相交于点O，下列结论错误的是(　　)A．OA＝OC，OB＝ODB．当AB＝CD时，四边形ABCD是菱形C．当∠ABC＝90°时，四边形ABCD是矩形D．当AC＝BD且AC⊥BD时，四边形ABCD是正方形
9．【2021·娄底】如图，点E、F在矩形ABCD的对角线BD所在的直线上，BE＝DF，则四边形AECF是(　　)A．平行四边形 　　B．矩形C．菱形　　 　　D．正方形
10．【中考· 舟山】如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF＝45°.求证：矩形ABCD是正方形．
证明：∵△AEF是等边三角形，∴AE＝AF，∠AFE＝∠AEF＝60°，∵四边形ABCD是矩形，∴∠B＝∠D＝∠C＝90°.又∵∠CEF＝45°，∴∠CFE＝45°，∴∠BEA＝∠DFA＝180°－45°－60°＝75°.在△BEA和△DFA中，∠BEA＝∠DFA，∠B＝∠D，AE＝AF，∴△BEA≌△DFA(AAS)，∴AB＝AD，∴矩形ABCD是正方形．
11．【2021·扬州】如图，在△ABC中，∠BAC的平分线交BC于点D，DE∥AB，DF∥AC.(1)试判断四边形AFDE的形状，并说明理由；
解：四边形AFDE是菱形，理由如下：∵DE∥AB，DF∥AC，∴四边形AFDE是平行四边形．∵AD平分∠BAC，∴∠FAD＝∠EAD.∵DE∥AB，∴∠EDA＝∠FAD.∴∠EDA＝∠EAD. ∴AE＝DE.∴平行四边形AFDE是菱形．
(2)若∠BAC＝90°，且AD＝2 ，求四边形AFDE的面积．
12．【2021·衡阳】如图，点E为正方形ABCD外一点，∠AEB＝90°，将Rt△ABE绕A点逆时针方向旋转90°得到△ADF，DF的延长线交BE于H点．(1)试判定四边形AFHE的形状，并说明理由．
解：四边形AFHE是正方形，理由如下：∵Rt△ABE绕A点逆时针方向旋转90°得到△ADF，∴Rt△ABE≌Rt△ADF.∴AE＝AF，BE＝DF，∠AEB＝∠AFD＝90°，∠DAF＝∠BAE. ∴∠AFH＝90°.∵∠DAF＋∠FAB＝90°，∴∠BAE＋∠FAB＝90°，即∠FAE＝90°，∴四边形AFHE是矩形，又∵AE＝AF，∴矩形AFHE是正方形．
(2)已知BH＝7，BC＝13，求DH的长．
解：∵四边形AFHE和四边形ABCD都是正方形，∴AE＝EH＝FH，AB＝BC＝13.设AE＝x.在Rt△AEB中，AB2＝AE2＋BE2，即132＝x2＋(x＋7)2，解得x＝5(x＝－12舍去)，∴BE＝BH＋EH＝7＋5＝12，∴DF＝BE＝12.又∵DH＝DF＋FH，∴DH＝12＋5＝17.
13．【中考·天水】如图①，对角线互相垂直的四边形叫做垂美四边形．(1)概念理解：如图②，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；
解：四边形ABCD是垂美四边形．理由：连接BD，AC.∵AB＝AD，∴点A在线段BD的垂直平分线上．∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，即四边形ABCD是垂美四边形；
(2)性质探究：如图①，四边形ABCD的对角线AC，BD交于点O，AC⊥BD.试证明：AB2＋CD2＝AD2＋BC2；
证明：∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，由勾股定理，得AB2＋CD2＝AO2＋BO2＋CO2＋DO2，AD2＋BC2＝AO2＋DO2＋BO2＋CO2，∴AB2＋CD2＝AD2＋BC2；
(3)解决问题：如图③，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE.已知AC＝4，AB＝5，求GE的长．
解：如图，连接CG，BE，设CE与AB交于点M.∵四边形ACFG和四边形ABDE都是正方形，∴AG＝AC，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG＋∠BAC＝∠BAE＋∠BAC，即∠GAB＝∠CAE.