2020-2021学年3.1.1不等关系与不等式教课ppt课件

这是一份2020-2021学年3.1.1不等关系与不等式教课ppt课件，共15页。PPT课件主要包含了杭州湾跨海大桥效果图，引入新课，v≤40，实数大小的比较，实际问题不等关系，数学问题不等式，抽象概括等内容，欢迎下载使用。

通过以上图片，我们可以了解到，在现实世界和日常生活中, 存在着大量的不等关系，那么，在数学中，应该如何表示这种不等关系呢？
（1）上图是限速40km/h的路标，指示司机在前方路段行驶时，应使汽车的速度v不超过40km/h ，写成不等式是：_________.
1.在数学中用不等式表示不等关系
（2）某品牌酸奶的质量检查规定，酸奶中脂肪的含量 f 应不少于2.5%，蛋白质的含量 p 应不少于2.3%，用不等式组可以表示为：________________
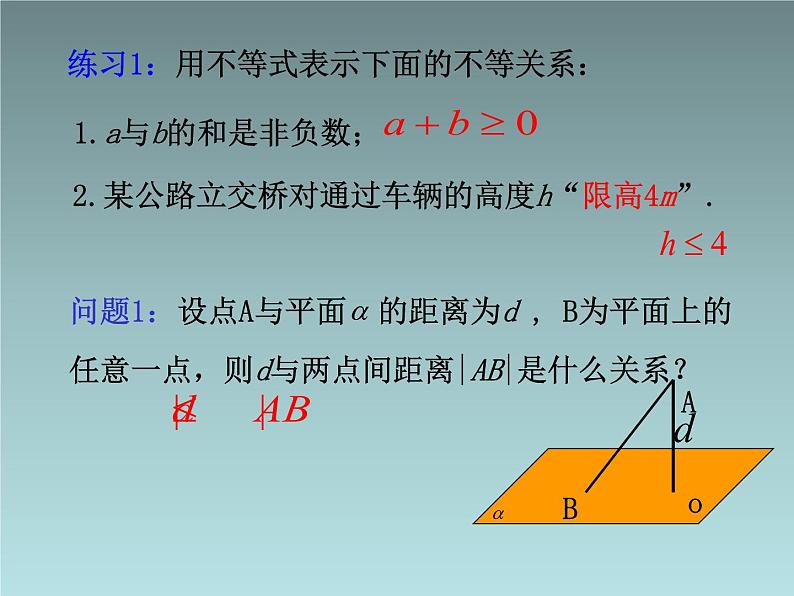
练习1：用不等式表示下面的不等关系：
1.a与b的和是非负数；
2.某公路立交桥对通过车辆的高度h“限高4m”.
问题2：某种杂志原以每本2.5元的价格销售，可以售出8万本.据市场调查，若单价每提高0.1元销售量就可能相应减少2000本.若把提价后杂志的定价设为 x 元，怎样用不等式表示销售的总收入仍不低于20万元呢？
问题3：某钢铁厂要把长度为4000mm的钢管截成500mm和600mm的两种规格.按照生产的要求，600mm的钢管的数量不能超过500mm钢管的3倍.怎样写出满足上述所有不等关系的不等式呢？
分析：假设截得500mm的钢管x 根，截得600mm的钢管y 根.根据题意，应当有什么样的不等关系呢？
(3)截得两种钢管的数量都不能为负.
(2)截得600mm钢管的数量不能超过500mm 的钢管数量的3倍；
(1)截得两种钢管的总长度不能超过4000mm；
要同时满足上面三个不等关系，可以用下面的不等式组来表示：
练习2：某年夏天，我国遭受特大洪灾，灾区学生小李家中经济发生困难，为帮助小李解决开学费用问题，小李所在班级学生（小李除外的x人 ）决定承担这笔费用（y元） . 若每人承担12元人民币，则多余84元；若每人承担10元，则不够；若每人承担11元，又多出40元以上.问怎样用不等式表示上述关系？
如果a-b是正数，则a>b；如果a>b，则a-b为正数；
如果a-b是负数，则a如果a-b 等于零，则a=b；如果a=b，则a-b 等于零;
例1．比较x2－x与x－2的大小.
解：(x2－x)－(x－2) = x2－2x +2
因为 (x－1)2≥0，
因此 x2－x > x－2.
练习3：比较(a+3) (a-5) 与 (a+2) (a-4)的大小.
(a+3) (a-5) < (a+2) (a-4)
= (x－1)2 +1
所以 (x－1)2+1>0，
即 (x2－x)－(x-- 2)>0，
… … … …判断符号
… … … …确定大小
小结 1. 建构数学
注意：在解决的时候要先读懂题意，找清不等词所联系的量，然后用适当的不等号连接起来，对含有多个不等关系的要用不等式组的形式表示，注意不重不漏。