初中数学人教版八年级下册18.1.1 平行四边形的性质评课课件ppt

这是一份初中数学人教版八年级下册18.1.1 平行四边形的性质评课课件ppt，共18页。PPT课件主要包含了学习目标，新课导入，探究一动手操作，试一试，拼一拼，课堂小结等内容，欢迎下载使用。
1.能画平行四边形，会用符号表示平行四边形. 2.能证明并运用“平行四边形对边相等、对角相等”的性质.
重点：平行四边形的定义及性质. 难点：运用性质解题.
这些都是日常生活中常见的情形，他们是否都有平行四边形的现象？
这些图形都有平行四边形的形象.
拿出剪好的两张对边平行的纸条，随意交叉叠放在一起，转动其中一张，重合的部分构成了一个怎样的四边形？
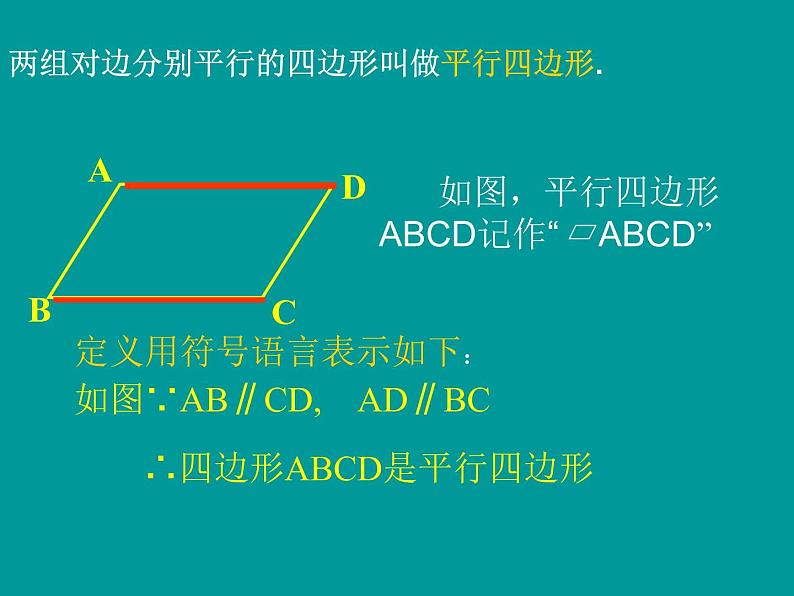
两组对边分别平行的四边形叫做平行四边形.
∴四边形ABCD是平行四边形
如图∵AB∥CD, AD∥BC
定义用符号语言表示如下：
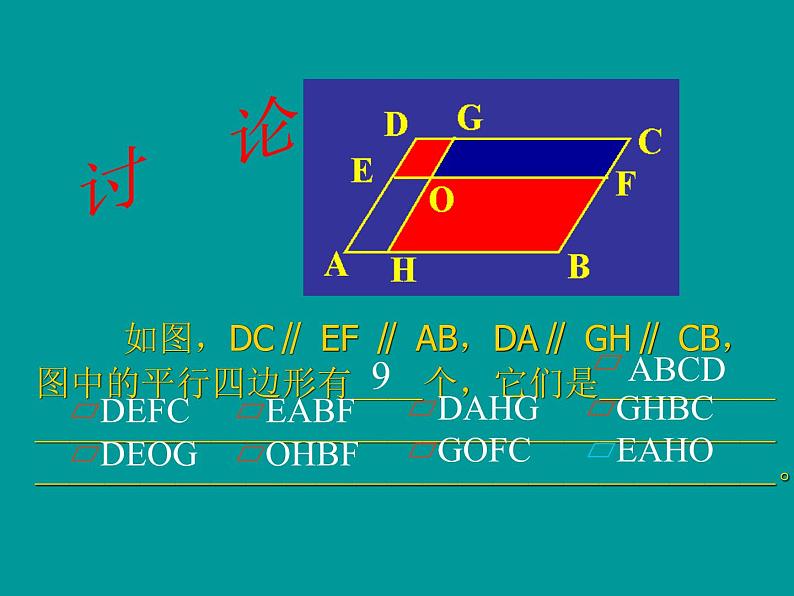
如图，DC∥ EF ∥ AB，DA∥ GH∥ CB，图中的平行四边形有＿＿个，它们是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
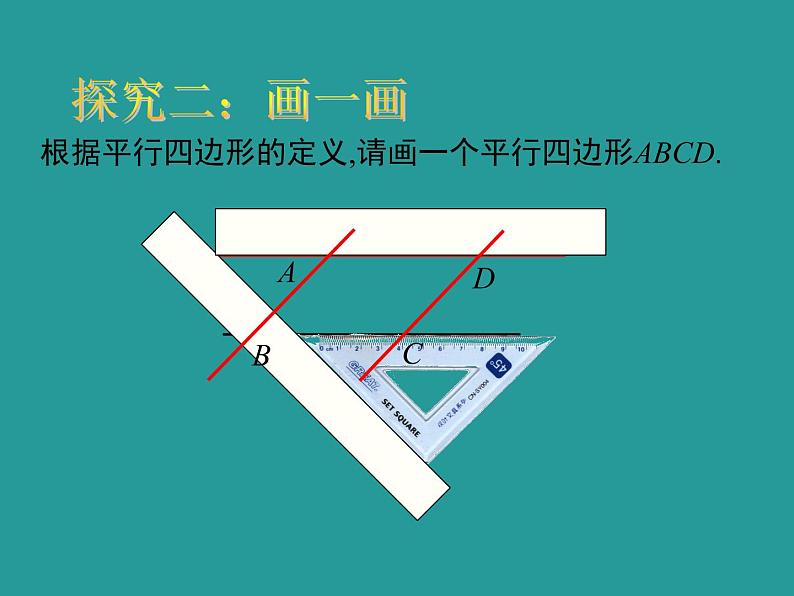
根据平行四边形的定义,请画一个平行四边形ABCD.
平行四边形的对边还有怎样的关系?平行四边形的对角有怎样的关系?
平行四边形： 两组对边分别相等 两组对角分别相等
合作交流，想方设法验证
证明：如图，连接AC.∵四边形ABCD是平行四边形,∴AD∥BC, AB∥CD∴∠1＝∠2, ∠3＝∠4∴∠BAD＝∠BCD在△ABC和△CDA中 ∠1＝∠2 AC＝CA ∠3＝∠4∴△ABC≌△CDA∴AD＝BC, AB＝DC, ∠B＝∠D∵∠BAD=∠1+∠4，∠BCD=∠2+∠3，∴∠BAD=∠BCD.
已知：四边形ABCD是平行四边形.求证:AD=BC,AB=CD,∠BAD=∠BCD,∠B＝∠D
思考 不添加辅助线，你能否直接运用平行四边形的定义，证明其对角相等？
证明：∵四边形ABCD是平行四边形,∴AD∥BC，AB ∥ CD,∴∠A+∠B=180°，∠A+∠D=180°，∴∠B=∠D.同理可得∠A=∠C.
平行四边形的对边相等．
平行四边形的性质除了对边互相平行以外，还有:
平行四边形的对角相等．
∵四边形ABCD是平行四边形
∴AD=BC，AB =CD
∴AD∥BC，AB ∥ CD
∴∠A=∠C，∠B=∠D
例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地，其中一条边AB长为8m，其他三条边各长多少?
解：∵ 四边形ABCD是平行四边形∴AB=CD, AD=BC∵AB=8m∴CD=8m 又AB+BC+CD+AD=36, ∴ AD=BC=10m
2.一个平行四边形的一个外 角是38°，这个平行四边形的每个内角的度数分别是多少？为什么？
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形？
小结： 平行四边形可以是由两个全等的三角形组成，因此在解决平行四边形的问题时，通常可以连结对角线转化为两个全等的三角形进行解题。
从拼图可以得到什么启示？
两组对边分别平行的四边形
两组对边分别平行，相等
两组对角分别相等，邻角互补