北师大版1 为什么要证明教学ppt课件

这是一份北师大版1 为什么要证明教学ppt课件，共24页。PPT课件主要包含了学习目标，导入新课，观察与思考，线是直还是曲，是静还是动，柱子是圆的还是方的，讲授新课，大数学家也有失误，做一做，位置关系等内容，欢迎下载使用。
1.了解推理的意义，知道要判断一个数学结论是否正确，必须进行推理。2.会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确。3.培养合作交流并探讨的学习品质,培养用科学的态度审视在数学活动中遇到的不确定结论的习惯。
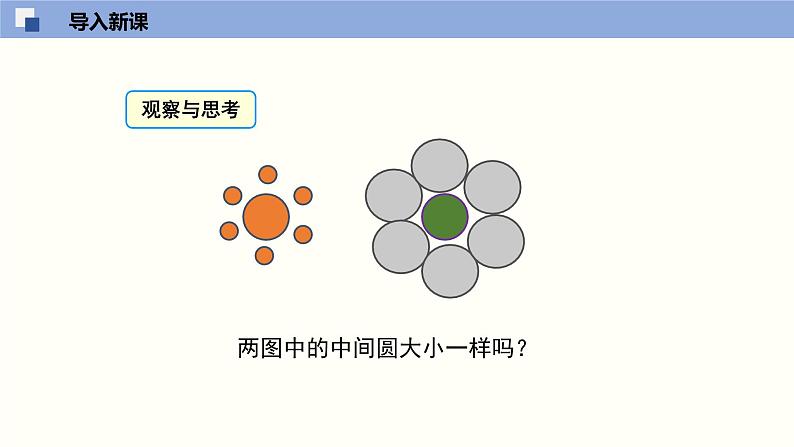
两图中的中间圆大小一样吗？
线段AB和CD长度完全相等,虽然它们看起来相差很大!
在现实生活中，我们常采用观察的方法来了解世界．在数学学习中，我们通过观察、度量、猜测来得到一些结论．那这样得到的结论都是正确的吗？如果是正确的，那么用什么方法说明它的正确性呢？
解：不一定都是正确的，如果正确，需要用推理证明的方法来说明它的正确性．
例：如图，把地球看成球形，假如用一根比地球赤道长1m的铁丝将地球赤道围起来，铁丝与地球赤道之间的间隙能有多大？能放进一个拳头吗？
别太信任你的眼睛和直觉哟！
举出反例是检验错误数学结论的有效方法.

这个故事告诉我们： 1. 学习欧拉的求实精神与严谨的科学态度.
2.没有严格的推理，仅由若干特例归纳、猜测的结论可能潜藏着错误，未必正确.
3.要证明一个结论是错误的，举反例就是一种常用方法.
（1）代数式n2-n+11的值是质数吗？取n=0,1,2,3,4,5试一试,你能否由此得到结论：对于所有的自然数n，n2-n+11的值都是质数？与同伴进行交流.
当n=11时,n2-n+11的值为121=112，所以，对于所有自然数n,n2-n+11的值未必都是质数.
（2）如图7-4，在△ABC中，点D，E分别是AB,AC的中点，连接DE. DE与BC有怎样的位置关系和数量关系？请你先猜一猜，再设法检验你的猜想.
你能肯定你的结论对所有的△ABC都成立吗？
结论:要判断一个数学结论是否正确,仅仅依靠经验、观察和实验是不够的，必须有根有据的进行推理即证明. 常用的证明方法:正面证明和举反例 思考:(1)在数学学习中,你用到过推理吗?举例说明. (2)在日常生活中,你用到过推理吗?举例说明.
1. 甲、乙、丙、丁4人进行乒乓球单循环比赛（每两个人都要比赛一场），结果甲胜了丁，并且甲、乙、丙胜的场次相同，则丁胜的场次是（　　）A． 3 B． 2 C． 1 D．0
2.下列问题用到推理的是（ ）A.根据a=10，b=10,得到a=bB.观察得到三角形有三个角C.老师告诉我们关于金字塔的许多奥秘D.由经验可知过两点有且只有一条直线
3.当x为任意实数时,x2+4x+5的值都大于零吗?
解：x2+4x+5=x2+4x+4+1=(x+2)2+1.因为(x+2)2≥0,所以(x+2)2+1>0.所以当x为任意实数时,x2+4x+5的值都大于零.
4.当n为正整数时，n2+3n+1的值一定是质数吗？
解：不是，当n=6时， n2+3n+1=55不是质数.
5.四位同学参加数学知识竞赛活动，分别获得第一、二、三、四名，大家猜测谁得第几名时，明明说：“甲得第一，乙得第二”；文文说：“甲得第二，丁得第四”；凡凡说：“丙得第二，丁得第三”．名次公布后，他们每人都只猜对了一半，那么甲、乙、丙、丁的名次顺序为　 　．（按一、二、三、四的名次排序）
【答案】甲、丙、乙、丁【解答】解：因为他们每人只猜对一半，可以先假设明明说“甲得第一”是正确的，由此推导：明明：甲得第一→文文：丁得第四→凡凡：丙得第二→乙得第三，成立；若假设明明说“乙得第二”是正确的，由此进行推导：明明：乙得第二→文文：丁得第四→凡凡：丙得第二，矛盾．所以甲、乙、丙、丁的名次顺序为甲、丙、乙、丁．故答案为：甲、丙、乙、丁．
6.某学校举办科技节活动，有甲、乙、丙、丁四个团队参加“智能机器人“项目比赛，该项目只设置一个一等奖，在评奖揭晓前，小张、小王、小李、小赵四位同学对这四个参赛团队获奖结果预测如下：小张说：“甲或乙团队获得一等奖”；小王说：“丁团队获得一等奖”；小李说：“乙、丙两个团均示队获得一等奖”；小赵说：“甲团队获得一等奖”．若这四位同学只有两位预测结果是对的，则获得一等奖的团队是　　　．
【答案】丁【解答】解：①若获得一等奖的团队是甲团队，则小张、小王、小赵预测结果是对的，与题设矛盾，即假设错误，②若获得一等奖的团队是乙团队，则小王预测结果是对的，与题设矛盾，即假设错误，③若获得一等奖的团队是丙团队，则四人预测结果都是错的，与题设矛盾，即假设错误，④若获得一等奖的团队是丁团队，则小李、小赵预测结果是对的，与题设相符，即假设正确，即获得一等奖的团队是：丁．故答案为：丁．
数学结论必须经过严格的论证