高中数学北师大版必修41同角三角函数的基本关系教学课件ppt

这是一份高中数学北师大版必修41同角三角函数的基本关系教学课件ppt，文件包含第3章1ppt、第3章1doc等2份课件配套教学资源，其中PPT共50页， 欢迎下载使用。
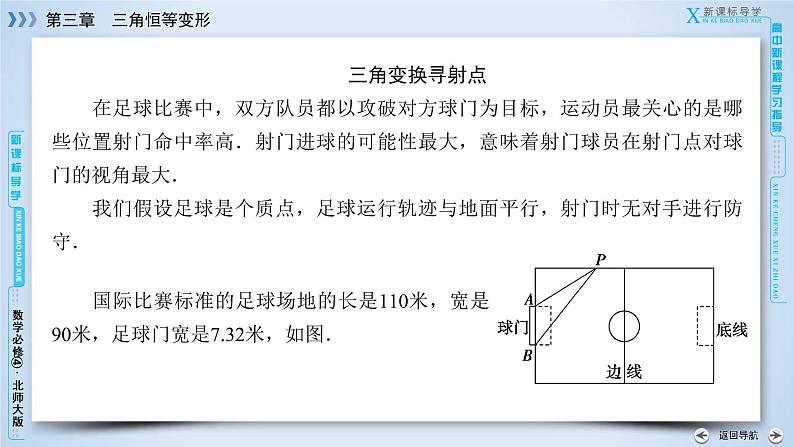
三角变换寻射点在足球比赛中，双方队员都以攻破对方球门为目标，运动员最关心的是哪些位置射门命中率高．射门进球的可能性最大，意味着射门球员在射门点对球门的视角最大．我们假设足球是个质点，足球运行轨迹与地面平行，射门时无对手进行防守．
国际比赛标准的足球场地的长是110米，宽是90米，足球门宽是7.32米，如图．
由平面几何知识可知，沿边线总可找到一点P，使得∠APB为最大(如图)．大家知道，队员技术水平一定的情况下，∠APB越大，在P点射门的命中率就越大，因此，我们称使得∠APB最大的点P为足球射门最佳点．那么在足球场内，哪些点属于足球射门最佳点呢？要解决这个问题就要用到数学中的三角恒等变形等知识．
§1 同角三角函数的基本关系
sin 2α＋cs 2α＝1　
4．化简sin 2α＋sin 2β－sin 2αsin 2β＋cs 2αcs 2β＝_____.[解析]　原式＝sin 2α(1－sin 2β)＋sin 2β＋cs 2αcs 2β＝sin 2αcs 2β＋cs 2αcs 2β＋sin 2β＝cs 2β(sin 2α＋cs 2α)＋sin 2β＝1.
命题方向1　⇨利用同角三角函数的关系求值
命题方向2　⇨关于sin α，cs α齐次式的求值
『规律总结』　关于sin α，cs α的齐次式的求值问题关于sin α，cs α的齐次式就是式子中的每一项都是关于sin α，cs α的式子，且它们的次数之和相同，其求解策略为：可用cs nα(n∈N＋)去除原式分子、分母的各项，这样可以将原式化为关于tan α的表达式，再整体代入tan α＝m的值，从而完成求值任务．
命题方向3　⇨三角函数式的化简
『规律总结』　化简三角函数式常用的方法有：(1)化切为弦，即把非正、余弦的函数都化成正、余弦函数，从而减少函数名称，达到化简的目的．(2)对于含有根号的，常把根号下的式子化成完全平方式，然后去根号达到化简的目的．(3)对于化简含高次的三角函数式，往往借助因式分解，或构造sin 2α＋cs 2α＝1，以降低函数次数，达到化简的目的．
[思路分析]　本题有多种证明方法，其共同点是“盯住目标，逐渐转化．”
『规律总结』　证法一是由左到右，以右式为果，左式通分，分子因式分解以产生因子cs α－sin α.此时，分子还缺少“2”这个因子，多余1＋sin α＋cs α这个因子，故分子分母同乘2，并尽量设法使分母产生1＋sin α＋cs α，以便约分．证法二是因右式分母有因子1＋sin α＋cs α，故将左式分子分母同乘1＋sin α＋cs α.证法三中证明的关键是使左、右两边变为同分母，而1＋sin α＋cs α是最简形式，故想到利用等比性质化简为同分母．
〔跟踪练习4〕求证：2(1－sin α)(1＋cs α)＝(1－sin α＋cs α)2.[证明]　证法一：左边＝1＋1－2sin α＋2cs α－2sin αcs α＝1＋sin 2α＋cs 2α－2sin α＋2cs α－2sin αcs α＝(1－sin α＋cs α)2＝右边．证法二：右边＝1＋sin 2α＋cs 2α－2sin α＋2cs α－2sin αcs α＝2(1－sin α＋cs α－sin αcs α)＝2(1－sin α)(1＋cs α)＝左边．证法三：右边－左边＝(1－sin α)2＋cs 2α＋2cs α(1－sin α)－2(1－sin α)(1＋cs α)＝(1－sin α)2＋cs 2α－2(1－sin α)＝－(1－sin α)(1＋sin α)＋cs 2α＝0.
忽略隐含条件导致出错　
『规律总结』　在应用三角公式时，应注意各公式中角的范围．其次把三角函数式隐含的条件尽可能挖掘出来，这样才不会出现漏解或增解．
－(sin 4＋cs 4)