高中北师大版第三章 三角恒等变换综合与测试教学演示课件ppt

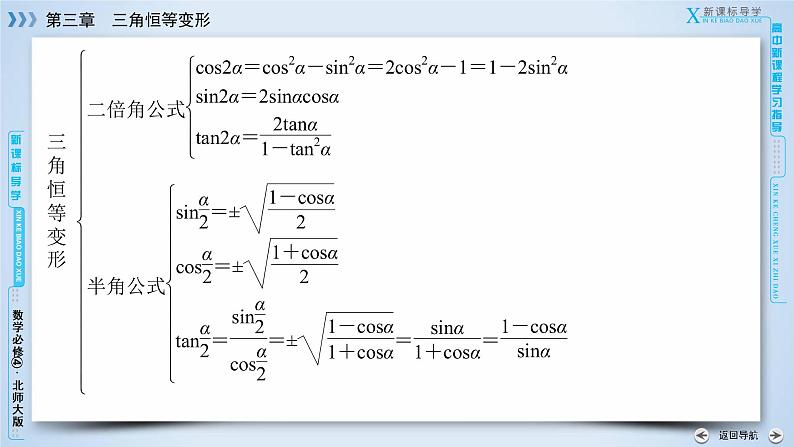
这是一份高中北师大版第三章 三角恒等变换综合与测试教学演示课件ppt，共51页。PPT课件主要包含了第三章，三角恒等变形，章末整合提升，知识结构，知识梳理，专题探究，典例1，典例2，专题三⇨求角的大小，典例3等内容，欢迎下载使用。
通过本章学习，重点掌握以下几个方面：1．三角函数式求值三角函数式的求值包括三种类型：给角求值，给值求值，给值求角．(1)给角求值给角求值的解法规律是恰当地应用诱导公式，合理地进行角的变形，恰当地应用和角与差角的三角函数公式、二倍角公式、半角公式，使其转化为特殊角的三角函数值的求解问题．给角求值中要注意当角较大时，应先利用诱导公式，这样能使角之间的关系更明确，这也是给角求值的技巧之一．技巧之二是进行角变换，将其中一个角用另两个角(已知角或特殊角)表示出来，减少未知角的个数．
(2)给值求值给值求值这类问题的解法规律是将所给的一个或几个三角函数式根据问题的需要进行恒等变形，使其转化为所求函数式能够使用的条件，然后用代入法求出三角函数式的值．也可以将所求的函数式经过适当的变形后，再利用条件，即给值求值的方法是代入法或恒等变形法．(3)给值求角给值求角这类问题的解法规律是根据已知条件求出该角的某种三角函数值，并根据已知条件判断出所求的角的范围，根据三角函数值及角的范围确定出角的大小．给值求角的难点是缩小角的范围，角的范围必须缩小到该三角函数的一个单调区间内，或在所确定的范围内，满足条件的角只有一个．
2．三角函数式的化简三角函数式的化简是对给定的三角函数式通过适当的三角变形，使之取得较简单的形式．化简三角函数式的常用方法有：(1)直接应用公式，(2)切化弦，(3)异角化同角，(4)特殊值与特殊角的三角函数互化，(5)通分、约分，(6)配方去根号．3．三角恒等式的证明三角恒等式的证明，就是应用三角公式，通过适当的恒等变形，消除三角恒等式两端结构上的差异，这些差异可从以下几方面入手：(1)角的差异，(2)三角函数名称的差异，(3)三角函数式结构形式上的差异．针对上面的差异，选择合适的方法进行等价转化．
证明三角恒等式的常用方法有：左右互推、左右归一、恒等变形、分析法、综合法等．三角恒等式的证明可分为两类：不附条件的三角恒等式的证明和附条件的三角恒等式的证明．不附条件的三角恒等式证明多用综合法、分析法、恒等变形等．附条件的三角恒等式的证明关键在于恰当、合理地应用条件，或通过变形观察所附条件与要证等式之间的联系，找到问题的突破口，常用代入法或消元法证明．
4．注意的问题(1)本章公式较多，学好本章的关键，在于清楚各公式的来龙去脉，搞明白各式之间的内在联系，把握公式的结构，这样才能准确应用公式，同时注意公式的逆用、变形应用．(2)转化思想是实施三角变形的主导思想，变形包括函数名称的变形、角的变形、和与积的变形、幂的升降变形及“1”的变形等．(3)恒等变形前需分析已知式中角和函数名称的差异，寻求联系，实现转化．(4)掌握基本技巧，如切割化弦、异名化同名、异角化同角等．
三角函数求值问题主要有三种类型，给角求值，给值求值和给值求角．给角求值一般是利用和、差、倍角公式进行变换，使其出现特殊角，若为非特殊角，则应变为可消去或约分的情况，从而求出其值．给值求值一般首先要先化简所求式子，弄清实际所求，或变为已知的式子，寻找已知与所求的联系，再求值．给值求角就是在给值求值的基础上，借助角的范围，求出角的值．
专题一　⇨三角函数式的化简与求值
[思路分析]　思路1——见到平方式就降幂；思路2——拆角80°＝60°＋20°；思路3——构造对偶式．
专题二　⇨三角函数式的条件求值
『规律总结』　(1)此类问题的解题思路是找出已知角与未知角的联系．(2)此类问题的解题步骤：①讨论角的范围；②求出指定范围内的角的三角函数值；③根据已知角与未知角的联系，利用和角公式与差角公式求值．
已知向量a＝(sin x，cs x)，b＝(sin x，sin x)，c＝(－1，0)．
专题四　⇨三角与向量的综合问题
『规律总结』　三角函数与向量结合是近几年高考的热点，主要从两方面考查：(1)利用向量的定义、公式，通过向量的运算，将向量条件转化为三角函数的条件，然后通过三角函数变换解决问题；(2)在三角函数与向量的关联点(角与距离)处设置问题，把三角函数中的角与向量的夹角统一为一类问题．
5．设A，B，C是△ABC的三个内角，且tan A，tan B是方程 3x2－5x＋1＝0的两个实数根，则△ABC是(　　)A．等边三角形　　B．等腰直角三角形C．锐角三角形　　D．钝角三角形
三、解答题10．设一元二次方程mx2＋(2m－1)x＋(m＋1)＝0的两根为tan α，tan β，求tan (α＋β)的取值范围．