





高中人教版新课标A第一章 空间几何体综合与测试教学课件ppt
展开空间几何体的三视图、直观图以及两者之间的转化是本章的难点,也是重点.解题需要依据它们的概念及画法规则,同时还要注意空间想象能力的运用.三视图和直观图是空间几何体的两种不同的表现形式.这两种不同的表现形式能够帮助我们从不同侧面、不同角度认识几何体的结构特征,进而研究几何体的有关性质.三视图和直观图联系密切,由空间几何体的直观图可以画出它的三视图,同样由空间几何体的三视图可以想象并画出这个几何体的直观图.直观图是在某一定点观察到的图形,三视图是从几何体的正前方、正左方、正上方观察到的几何体轮廓线的正投影围成的平面图形.
专题一 ⇨几何体的三视图和直观图
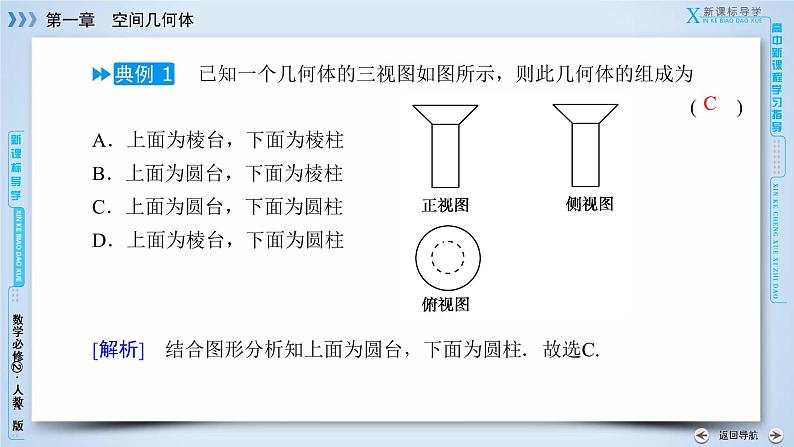
已知一个几何体的三视图如图所示,则此几何体的组成为( )A.上面为棱台,下面为棱柱B.上面为圆台,下面为棱柱C.上面为圆台,下面为圆柱D.上面为棱台,下面为圆柱
[解析] 结合图形分析知上面为圆台,下面为圆柱.故选C.
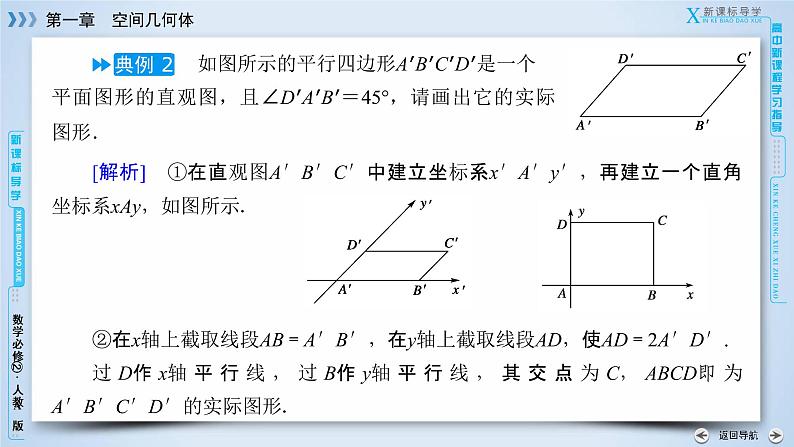
如图所示的平行四边形A′B′C′D′是一个平面图形的直观图,且∠D′A′B′=45°,请画出它的实际图形.
[解析] ①在直观图A′B′C′中建立坐标系x′A′y′,再建立一个直角坐标系xAy,如图所示.②在x轴上截取线段AB=A′B′,在y轴上截取线段AD,使AD=2A′D′.过D作x轴平行线,过B作y轴平行线,其交点为C,ABCD即为A′B′C′D′的实际图形.
几何体的表面积和体积的计算是现实生活中经常遇到的问题,如制作物体的下料问题、材料最省问题、相同材料容积最大问题,都涉及表面积和体积的计算.特别是特殊的柱、锥、台,在计算中要注意其中矩形、梯形及直角三角形等重要的平面图形的作用,对于圆柱、圆锥、圆台,要重视旋转轴所在的轴截面、底面圆的作用.(1)在求解空间几何体的表面积问题时,常将空间几何体的表(侧)面展开,化折(曲)为直,将空间图形问题转化为平面图形问题,这是解决立体几何问题的常用方法.
专题二 ⇨柱体、锥体、台体的表面积和体积
(2)将一些不规则的几何体进行修补(补形法),或者将一些几何体进行分割(分割法),或者通过变换顶点和底面,利用体积相等求解(等积法)等是求空间几何体体积的重要思想方法.例如,常见的将三棱柱补成四棱柱,四棱锥分割成三棱锥,再利用四棱柱、三棱锥的特殊性求体积.又如将三棱锥的顶点和底面进行交换,利用体积相等求体积或求几何体的高.
如图所示为一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的表面积为( )
一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1、V2、V3、V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )A.V1<V2<V4<V3 B.V1<V3<V2<V4C.V2<V1<V3<V4 D.V2<V3<V1<V4
球与其他几何体组成的几何体通常在试题中以相切或相接的形式出现,解决此类问题常常利用截面来表现这两个几何体之间的关系,从而将空间问题转化为平面问题.(1)作适当的截面(如轴截面等)时,对于球内接长方体、正方体,则截面一要过圆心,二要过长方体或正方体的两条对角线,才有利于解题.(2)对于“内切”和“外接”等问题,首先要弄清几何体之间的相互关系,主要是指特殊的点、线、面之间的关系,然后把相关的元素放到这些关系中来解决.
专题三 ⇨球与其他几何体的简单组合体问题
如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( )
在解决具体问题时,常把复杂的、生疏的、抽象的、困难的、未知的问题化成简单的、熟悉的、具体的、容易的、已知的问题来解决,这种数学思想叫转化与化归的思想.(1)“化曲为直”是解决立体几何问题最基本和最常用的方法,解决的关键是在空间图形展开后,弄清几何体中的有关点、线在展开图中的相应位置关系.几何体表面上两点间的最小距离问题常常转化为求其展开图中的直线段长.
专题四 ⇨转化与化归思想
(2)体积的求解与计算是立体几何学习的重点,其方法灵活多样,但转化与化归的思想一直贯穿其中.①将不规则的几何体通过分割或补形,将其转化为规则几何体的体积问题;②三棱锥通过转化底面和顶点从而达到求体积的目的.
如下图1所示,已知三棱柱ABC-A′B′C′,侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a.
设一个圆锥的底面积为10,它的侧面展开成平面图后为一个半圆,则此圆锥的侧面积是( )A.10 B.20C.30 D.40
专题五 ⇨自招竞赛,能力拔高
已知一扇形的圆心角为60°,面积为6π,将它围成一个圆锥,则此圆锥的表面积是( )[思路分析] 根据已知条件求出圆锥的底面半径,从而可求底面积,侧面积(即扇形面积)和底面积相加即得表面积.
在长方体中,a,b,c为棱长,a>b>c,求沿长方体表面从P到Q的最小距离(P,Q是长方体对角线的两个端点).
证明:一个四面体中至少存在一个顶点,使得从其出发的三条棱能够组成一个三角形.[解析] 如图所示,不妨设AB是四面体ABCD的六条棱中最长的一条,考虑△ABD,△ABC中,AD+DB>AB,AC+CB>AB,故AD+DB+AC+CB>2AB,即(AD+AC)+(BD+CB)>2AB,所以AD+AC,BD+CB中至少有一个大于AB.不妨设AD+AC>AB,则从A出发的三条棱AB,AD,AC能够组成一个三角形.
体积为1的正四面体被放置于一个正方体中,则此正方体体积的最小值是______.
如图所示,正四棱锥P-ABCD中,B1为PB的中点,D1为PD的中点,求两个棱锥A-B1CD1,P-ABCD的体积之比.[思路分析] 对于三棱锥A-B1CD1,无论将哪个三角形作为底面都不方便计算体积,故考虑用间接法,即考虑其余四个小三棱锥D1-ACD,B1-ABC,P-B1CD1,P-AB1D1与原四棱锥P-ABCD的体积比.
高中人教版新课标A第二章 统计综合与测试课堂教学课件ppt: 这是一份高中人教版新课标A第二章 统计综合与测试课堂教学课件ppt,共38页。PPT课件主要包含了第二章,章末整合提升,知识网络,专题突破,典例1,典例2,典例3,典例4,典例5,典例6等内容,欢迎下载使用。
高中人教版新课标A第三章 函数的应用综合与测试集体备课ppt课件: 这是一份高中人教版新课标A第三章 函数的应用综合与测试集体备课ppt课件,共6页。
高中数学人教版新课标A必修1第三章 函数的应用综合与测试教案配套课件ppt: 这是一份高中数学人教版新课标A必修1第三章 函数的应用综合与测试教案配套课件ppt,共30页。PPT课件主要包含了第三章,函数的应用,章末整合提升,知识结构,要点归纳,专题突破,典例1,典例2,典例3,典例4等内容,欢迎下载使用。













