

广东省揭阳市揭西县2021-2022学年七年级上学期期末数学试卷(word版 含答案)
展开这是一份广东省揭阳市揭西县2021-2022学年七年级上学期期末数学试卷(word版 含答案),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.2022的相反数是( )
A.2022B.C.﹣2022D.﹣
2.下列计算正确的是( )
A.2xy﹣xy=1B.3ab﹣a=3b
C.3m3n﹣nm3=2m3nD.a3﹣a2=a
3.2021年国庆档热门影片《长津湖》以抗美援朝战争第二次战役中的长津湖战役为背景,讲述了中国人民志
愿军赴朝作战,奋勇杀敌的历史,上映16天票房突破3600000000元,将数据3600000000用科学记数法表示为( )
A.36×108B.0.36×108C.3.6×109D.0.36×1010
4.某班数学老师结合中国共产党建党一百周年,在班级内组织了一堂“正方体展开图猜猜看”活动课,下图是该正方体展开图的一种,那么原正方体中,与“党”字所在面对面上的汉字是( )
A.礼B.年C.百D.赞
5.若x是﹣3的相反数,|y|=5,则x+y的值为( )
A.8或﹣2B.8C.﹣8或2D.2
6.如图,在数轴上有A、B、C、D四个点,分别表示不同的四个数,若从这四点中选一点做原点,使得其余三点表示的数中有两个正数和一个负数,则这个点是( )
A.点AB.点BC.点CD.点D
7.以下调查中,最适合用来全面调查的是( )
A.调查柳江流域水质情况
B.了解全国中学生的心理健康状况
C.了解全班学生的身高情况
D.调查春节联欢晚会收视率
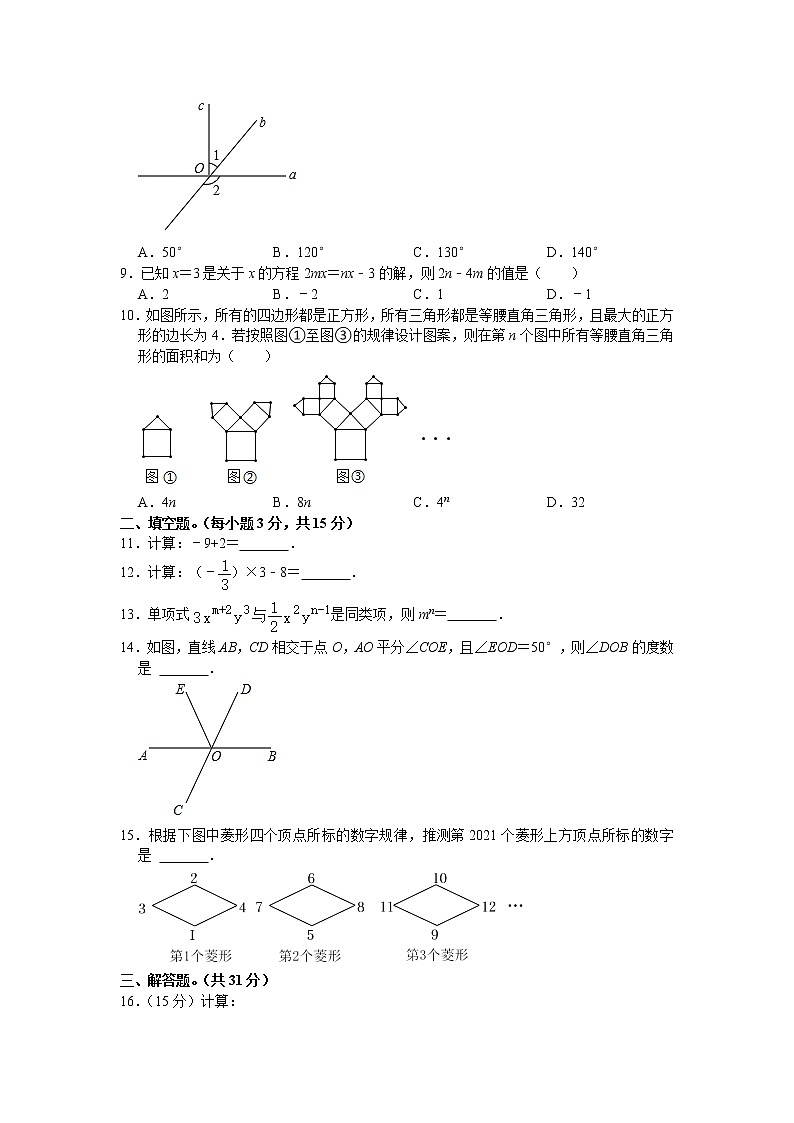
8.如图,直线a,b相交于点O,射线c⊥a,垂足为点O,若∠1=40°,则∠2的度数为( )
A.50°B.120°C.130°D.140°
9.已知x=3是关于x的方程2mx=nx﹣3的解,则2n﹣4m的值是( )
A.2B.﹣2C.1D.﹣1
10.如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第n个图中所有等腰直角三角形的面积和为( )
A.4nB.8nC.4nD.32
二、填空题。(每小题3分,共15分)
11.计算:﹣9+2= .
12.计算:(﹣)×3﹣8= .
13.单项式是同类项,则mn= .
14.如图,直线AB,CD相交于点O,AO平分∠COE,且∠EOD=50°,则∠DOB的度数是 .
15.根据下图中菱形四个顶点所标的数字规律,推测第2021个菱形上方顶点所标的数字是 .
三、解答题。(共31分)
16.(15分)计算:
(1)7﹣(﹣8)+(﹣9)﹣6;
(2);
(3)4(a﹣b)+(2a﹣3b).
17.(6分)先化简,再求值:
(a2﹣ab﹣7)﹣(﹣4a2+2ab+7),其中a=2,b=.
18.(10分)解方程
(1)x﹣2=5x+6
(2)2x﹣=3﹣.
六.解答题。(每小题8分,共24分)
19.(8分)春节期间,某超市出售的桂圆和芒果,单价分别为每千克26元和22元,李叔叔购买这两种水果共30千克,共花了708元,请问李叔叔购买这两种水果各多少千克?
20.(8分)如图所示,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点,若AB=15,AD=2BE,求线段CE的长.
21.(8分)【知识回顾】
七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是:把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.
【理解应用】
(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,求m值;
(2)已知A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,且3A+6B的值与x无关,求y的值;
【能力提升】
(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
参考答案与试题解析
一、选择题。(每小题3分,共30分)
1.2022的相反数是( )
A.2022B.C.﹣2022D.﹣
【分析】根据相反数的定义即可得出答案.
【解答】解:2022的相反数是﹣2022.
故选:C.
【点评】本题考查了相反数,解题的关键是掌握只有符号不同的两个数互为相反数.
2.下列计算正确的是( )
A.2xy﹣xy=1B.3ab﹣a=3b
C.3m3n﹣nm3=2m3nD.a3﹣a2=a
【分析】合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变.据此判断即可.
【解答】解:A.2xy﹣xy=xy,故本选项不合题意;
B.3ab与﹣a不是同类项,所以不能合并,故本选项不合题意;
C.3m3n﹣nm3=2m3n,故本选项符合题意;
D.a3与﹣a2不是同类项,所以不能合并,故本选项不合题意;
故选:C.
【点评】本题考查了合并同类项,掌握合并同类项法则是解答本题的关键.
3.2021年国庆档热门影片《长津湖》以抗美援朝战争第二次战役中的长津湖战役为背景,讲述了中国人民志
愿军赴朝作战,奋勇杀敌的历史,上映16天票房突破3600000000元,将数据3600000000用科学记数法表示为( )
A.36×108B.0.36×108C.3.6×109D.0.36×1010
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:3600000000=3.6×109.
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,正确确定a的值以及n的值是解决问题的关键.
4.某班数学老师结合中国共产党建党一百周年,在班级内组织了一堂“正方体展开图猜猜看”活动课,下图是该正方体展开图的一种,那么原正方体中,与“党”字所在面对面上的汉字是( )
A.礼B.年C.百D.赞
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“礼”与“赞”是相对面,
“建”与“百”是相对面,
“党”与“年”是相对面;
故选:B.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手.
5.若x是﹣3的相反数,|y|=5,则x+y的值为( )
A.8或﹣2B.8C.﹣8或2D.2
【分析】直接利用相反数的性质以及绝对值的性质分别得出x,y的值,进而得出答案.
【解答】解:∵x是﹣3的相反数,|y|=5,
∴x=3,y=±5,
则x+y的值为:3+5=8或3﹣5=﹣2.
故选:A.
【点评】此题主要考查了相反数的性质以及绝对值的性质,正确得出x,y的值是解题关键.
6.如图,在数轴上有A、B、C、D四个点,分别表示不同的四个数,若从这四点中选一点做原点,使得其余三点表示的数中有两个正数和一个负数,则这个点是( )
A.点AB.点BC.点CD.点D
【分析】根据数轴上的点原点右边表示正数,原点左边表示负数解决此题.
【解答】解:A.当A为原点,则剩余三个点表示的数均是正数,故A不合题意.
B.当B为原点,则A表示负数,C与D表示正数,故B符合题意.
C.当C为原点,则A与B表示负数,D表示正数,故C不符合题意.
D.当D为原点,A、B与C表示负数,故D不符合题意.
故选:B.
【点评】本题主要考查数轴,熟练掌握数轴上的点表示的数是解决本题的关键.
7.以下调查中,最适合用来全面调查的是( )
A.调查柳江流域水质情况
B.了解全国中学生的心理健康状况
C.了解全班学生的身高情况
D.调查春节联欢晚会收视率
【分析】根据全面调查的意义,结合具体问题情境逐项进行判断即可.
【解答】解:A、调查柳江流域水质情况,适合抽样调查,故本选项不符合题意;
B、了解全国中学生的心理健康状况,适合抽样调查,故本选项不符合题意;
C、了解全班学生的身高情况,适合普查,故本选项符合题意;
D、调查春节联欢晚会收视率,适合抽样调查,故本选项不符合题意.
故选:C.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
8.如图,直线a,b相交于点O,射线c⊥a,垂足为点O,若∠1=40°,则∠2的度数为( )
A.50°B.120°C.130°D.140°
【分析】根据对顶角和垂线的性质解答即可.
【解答】解:∵c⊥a,
∴∠AOB=90°,
∵∠1=40°,
∴∠AOC=90°+40°=130°,
∵∠2=∠AOC,
∴∠2=130°.
故选:C.
【点评】此题考查垂线的性质,对顶角的性质,关键是根据垂线的性质及角的和差关系得出∠AOC=130°.
9.已知x=3是关于x的方程2mx=nx﹣3的解,则2n﹣4m的值是( )
A.2B.﹣2C.1D.﹣1
【分析】把x=3代入方程,整理确定出2m﹣n的值,原式变形后代入计算即可求出值.
【解答】解:把x=3代入方程得:6m=3n﹣3,
整理得:2m﹣n=﹣1,
则原式=﹣2(2m﹣n)=2.
故选:A.
【点评】此题考查了一元一次方程的解,利用了整体代入的思想,方程的解即为能使方程左右两边相等的未知数的值.
10.如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第n个图中所有等腰直角三角形的面积和为( )
A.4nB.8nC.4nD.32
【分析】设第一个等腰三角形边长为a,第二个等腰三角形的边长为b,第三个等腰三角形的边长为c,如图,图④,图⑤,图⑥,由已知,由图④根据勾股定理可知a2+a2=42,即可计算出a2的值,根据三角形面积的计算方法即可的算出第一个等腰三角形的面积,由图⑤,根据勾股定理可得b2+b2=a2,即可算出b2的值,根据三角形的面积计算方法可计算出图⑤中三个等腰三角形的面积和,同理可计算出图⑥中共计6个等腰三角形面积和,根据三个面积和进行推理即可得出答案.
【解答】解:设第一个等腰三角形边长为a,第二个等腰三角形的边长为b,第三个等腰三角形的边长为c,
如图,图④,图⑤,图⑥,
由图④可知,
∵最大正方形的边长为4,
∴a2+a2=42,
∴第一个等腰三角形的面积为a•a==4,
由图⑤可知,
∵b2+b2=a2,
即2b2=8,
∴图⑤中三个等腰三角形的面积和为a2++b2=4+2+2=8,
由图⑥可知,
∵c2+c2=b2,
即2c2=2,
图⑥中共计6个等腰三角形面积和为a2++b2++++=4+2+2+1+1+1+1=12,
•••
由此推理,第n个图中所有等腰直角三角形的面积和为4n.
故选:A.
【点评】本题主要考查了勾股定理及图形的变化规律,熟练掌握勾股定理及图形的变化规律进行计算是解决本题的关键.
二、填空题。(每小题3分,共15分)
11.计算:﹣9+2= ﹣7 .
【分析】有理数加法法则:绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值.依此计算即可求解.
【解答】解:﹣9+2=﹣7.
故答案为:﹣7.
【点评】此题考查了有理数加法,在进行有理数加法运算时,首先判断两个加数的符号:是同号还是异号,是否有0.从而确定用那一条法则.在应用过程中,要牢记“先符号,后绝对值”.
12.计算:(﹣)×3﹣8= ﹣9 .
【分析】根据有理数的乘法和减法可以解答本题.
【解答】解:(﹣)×3﹣8
=(﹣1)﹣8
=﹣9,
故答案为:﹣9.
【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
13.单项式是同类项,则mn= 0 .
【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出m,n的值,再代入计算即可.
【解答】解:∵单项式是同类项,
∴m+2=2,n﹣1=3,
解得:m=0,n=4,
∴mn=04=0.
故答案为:0.
【点评】本题考查同类项的定义,关键是根据同类项的定义列出方程解答.
14.如图,直线AB,CD相交于点O,AO平分∠COE,且∠EOD=50°,则∠DOB的度数是 65° .
【分析】根据互为补角求出∠COE,再根据角平分线的意义求出∠AOC,由对顶角相等得出答案.
【解答】解:∵∠EOD=50°,
∴∠COE=180°﹣∠EOD=130°,
又∵AO平分∠COE,
∴∠AOC=∠AOE=∠COE=65°,
∴∠DOB=∠AOC=65°,
故答案为:65°.
【点评】本题考查互为补角以及角平分线的定义,掌握互为补角和角平分线的意义是正确计算的前提.
15.根据下图中菱形四个顶点所标的数字规律,推测第2021个菱形上方顶点所标的数字是 8082 .
【分析】由题意得:第n个菱形上方顶点所标的数字是2+(n﹣1)×4=4n﹣2,即可求解.
【解答】解:由题意得:第n个菱形上方顶点所标的数字是2+(n﹣1)×4=4n﹣2,
∴第2021个菱形上方顶点所标的数字是:4×2021﹣2=8082,
故答案为:8082.
【点评】本题考查了菱形的性质、规律型,找出菱形顶点上标数的变化规律是解题的关键.
三、解答题。(共31分)
16.(15分)计算:
(1)7﹣(﹣8)+(﹣9)﹣6;
(2);
(3)4(a﹣b)+(2a﹣3b).
【分析】(1)直接去括号,利用有理数的加减运算法则计算得出答案;
(2)直接利用有理数的混合运算法则分别化简,进而计算得出答案;
(3)直接去括号,再合并同类项得出答案.
【解答】解:(1)原式=7+8﹣9﹣6
=0;
(2)原式=﹣9÷3+(﹣)×12﹣1
=﹣3+(﹣2)﹣1
=﹣6;
(3)原式=4a﹣4b+2a﹣3b
=6a﹣7b.
【点评】此题主要考查了整式的加减以及有理数的混合运算,正确掌握相关运算法则是解题关键.
17.(6分)先化简,再求值:
(a2﹣ab﹣7)﹣(﹣4a2+2ab+7),其中a=2,b=.
【分析】先去括号,再合并同类项,然后将a=2,b=代入计算即可得出答案.
【解答】解:(a2﹣ab﹣7)﹣(﹣4a2+2ab+7)
=a2﹣ab﹣7+4a2﹣2ab﹣7
=5a2﹣3ab﹣14,
∵a=2,b=,
∴原式=5×22﹣3×2×﹣14
=20﹣9﹣14
=﹣3.
【点评】本题考查了整式的加减﹣化简求值,熟练掌握整式的加减及有理数的相关运算法则是解题的关键.
18.(10分)解方程
(1)x﹣2=5x+6
(2)2x﹣=3﹣.
【分析】(1)方程移项合并,将x系数化为1,即可求出解;
(2)方程去分母后,去括号,移项合并,将x系数化为1,即可求出解.
【解答】解:(1)移项合并得:﹣4x=8,
解得:x=﹣2;
(2)去分母得:20x﹣2(x﹣1)=30﹣5(x+2),
去括号得:20x﹣2x+2=30﹣5x﹣10,
移项合并得:23x=18,
解得:x=.
【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.
六.解答题。(每小题8分,共24分)
19.(8分)春节期间,某超市出售的桂圆和芒果,单价分别为每千克26元和22元,李叔叔购买这两种水果共30千克,共花了708元,请问李叔叔购买这两种水果各多少千克?
【分析】设购买了桂圆x千克,则购买芒果(30﹣x)千克.根据两种水果共花了708元,列出方程并解答即可.
【解答】解:设购买了桂圆x千克,则购买芒果(30﹣x)千克.
根据题意列方程得:26x+22(30﹣x)=708,
解得:x=12,30﹣x=18.
答:购买了桂圆12千克,购买芒果18千克.
【点评】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
20.(8分)如图所示,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点,若AB=15,AD=2BE,求线段CE的长.
【分析】首先设EB=x,根据线段中点的性质推出AD、DE关于x的表达式,即AD=DE=2x,由图形推出AD+DE+BE=15,即可得方程:x+2x+2x=15,通过解方程推出x=3,即BE=3,最后由BC=7.5,即可求出CE的长度.
【解答】解:设EB=x,则AD=2BE=2x,
∵点D为线段AE的中点,
∴AD=DE=2x,
∵AB=15,
∴AD+DE+BE=15,
∴x+2x+2x=15,
解方程得:x=3,即BE=3,
∵AB=15,C为AB中点,
∴BC=AB=7.5,
∴CE=BC﹣BE=7.5﹣3=4.5.
【点评】本题主要考查线段中点的性质,关键在于正确的进行计算,熟练运用数形结合的思想推出相关线段之间的数量关系.
21.(8分)【知识回顾】
七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是:把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.
【理解应用】
(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,求m值;
(2)已知A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,且3A+6B的值与x无关,求y的值;
【能力提升】
(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
【分析】(1)由题可知代数式的值与x的取值无关,所以含x项的系数为0,故将多项式整理为(2m﹣3)x﹣3m+2m2,令x系数为0,即可求出m;
(2)根据整式的混合运算顺序和法则化简3A+6B可得3x(5y﹣2)﹣9,根据其值与x无关得出5y﹣2=0,即可得出答案;
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),即可得到S1﹣S2关于x的代数式,根据取值与x可得a=2b.
【解答】解:(1)(2x﹣3)m+2m2﹣3x
=2mx﹣3m+2m2﹣3x
=(2m﹣3)x+2m2﹣3m,
∵其值与x的取值无关,
∴2m﹣3=0,
解得,m=,
答:当m=时,多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关;
(2)∵A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,
∴3A+6B=3[(2x+1)(x﹣1)﹣x(1﹣3y)]+6(﹣x2+xy﹣1)
=3(2x2﹣2x+x﹣1﹣x+3xy]﹣6x2+6xy﹣6
=6x2﹣6x+3x﹣3﹣3x+9xy﹣6x2+6xy﹣6
=15xy﹣6x﹣9
=3x(5y﹣2)﹣9,
∵3A+6B的值与x无关,
∴5y﹣2=0,即y=;
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2=a(x﹣3b)﹣2b(x﹣2a)=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变.
∴S1﹣S2取值与x无关,
∴a﹣2b=0
∴a=2b.
【点评】本题主要考查了多项式乘多项式,整式的化简求值,熟练掌握整式的混合运算顺序和法则及由题意得出关于y的方程是解题的关键.
相关试卷
这是一份2022-2023学年广东省揭阳市榕城区、揭西县七年级(下)期中数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2021-2022学年广东省揭阳市揭西县七年级(下)第二次质检数学试卷(解析版),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省揭阳市揭西县2022年八年级上学期期末数学试卷及答案,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













