高中数学北师大版必修23.1简单组合体的三视图图文课件ppt

这是一份高中数学北师大版必修23.1简单组合体的三视图图文课件ppt，文件包含13ppt、13doc等2份课件配套教学资源，其中PPT共47页， 欢迎下载使用。
参观上海世博会，看的最多的是什么？相信不少游客会异口同声地回答：电影．的确，无论是坐着看、站着看、转着看、躺着看、趴着看，影片已成为众多场馆的主要展示手段．纵观上海世博会场馆播放的影片，除了传统电影外，以高新技术打造的3D,4D电影比比皆是，屏幕更是从180度、360度直至720度，营造出令人震撼的视听效果．同学们，你们知道吗？电影的放映过程中就蕴含着丰富的视图知识．
1．三视图的画法要求(1)三视图的主视图、俯视图、左视图分别是从物体的__________、__________、__________看到的物体轮廓线的正投影围成的平面图形．
(2)一个物体的三视图的排列规则是：俯视图放在主视图的________，长度与主视图一样；左视图放在主视图的________，高度与主视图一样，宽度与俯视图的宽度一样．如图所示．
(3)记忆口诀：①长对正，高平齐，宽相等；②主左一样高，主俯一样长，俯左一样宽．(4)注意：在三视图中，分界线和可见轮廓线用______线画出，不可见轮廓线，用______线画出．
2．组合体的三视图(1)由基本几何体生成的组合体有两种基本形式：①将______________拼接成组合体．②从基本几何体中__________________构成组合体．(2)画简单组合体的三视图应注意两个问题：首先，确定主视、俯视、左视的________.同一物体放置的位置不同，所画的三视图可能________．其次，清楚简单组合体是由哪几个基本几何体组成的，并注意它们的组成方式，特别是它们的____________．
3．由三视图还原成实物图由三视图画直观图时，必须先观察__________，想象出具体形状，还原成__________，再画出直观图．
1．下列几何体各自的三视图中，有且仅有两个视图相同的是(　　)A．①②　B．①③　　C．①④　D．②④
[解析]　正方体的主视图、左视图、俯视图都为正方形；圆锥的主视图、左视图、俯视图依次为三角形、三角形、圆(含圆心)；三棱台的主视图、左视图、俯视图依次为梯形及上、下底中点的连线、梯形(不同于主视图)、三角形(内外两个对应顶点相连的三角形)；正四棱锥的主视图、左视图、俯视图依次为三角形、三角形、正方形及其两条对角线．
2．(新课标全国卷Ⅱ改编)如图所示，画四面体AB1CD1三视图中的主视图时，以面AA1D1D为投影面，则得到的主视图可以为(　　)
[解析]　显然AB1，AC，B1D1，CD1在面AA1D1D上的正投影分别为AA1，AD，A1D1，DD1，可知主视图的外轮廓为一个正方形，B1C为可见实线，AD1为不可见虚线．只有A符合．
3．如果一个几何体的主视图是矩形，则这个几何体不可能是(　　)A．棱柱B．棱锥C．棱台D．圆柱[解析]　棱锥的主视图不可能是矩形，故选B．
4．某物体的实物图如图(甲)所示，在其三视图中，图①是__________；图②是__________；图③是__________．
5．一个几何体的主视图为一个三角形，则这个几何体可能是下列几何体中的____________.(填入所有可能的几何体前的编号)①三棱锥　②四棱锥　③三棱柱　④四棱柱　⑤圆锥　⑥圆柱[解析]　只要判断主视图是不是三角形就行了，画出图形容易知道三棱锥、四棱锥、圆锥一定可以，对于三棱柱，只需要倒着放就可以了，所以①②③⑤均符合题目要求．
命题方向1　⇨简单几何体的三视图
　　　　　如图所示是截去一角的长方体，画出它的三视图．
[思路分析]　物体三个视图的构成都是矩形，长方体截角后，截面是一个三角形，在每个视图中反映为不同的三角形．
[解析]　该长方体的三视图为如图所示：
『规律总结』　1.画三视图时，首先确定主视、左视、俯视的方向，同一物体放置的位置不同，所画的三视图可能不同．一般主视方向确定了，则左视与俯视的方向也就确定了，在有的问题里，直接给出主视图，也是确定主视方向的一个方法．2．一个物体的三视图的排列规则是：俯视图放在主视图的下面，左视图放在主视图的右面．
〔跟踪练习1〕如图所示，图(1)是底面边长和侧棱长都是2cm的四棱锥，图(2)是上、下底面半径分别为1cm,2cm，高为2cm的圆台，分别画出它们的三视图．
[解析]　(1)四棱锥的三视图如图所示：
(2)圆台的三视图如下图所示：
命题方向2　⇨画简单组合体的三视图
　　　　　画出下列几何体的三视图(阴影面为主视面)．
[思路分析]　画简单组合体的三视图时，首先要认真观察，可以想象自己就站在物体的正前方、正上方、正左方，观察它是由哪些基本几何体组合而成的，它的外轮廓线是什么，然后再去画图．
[解析]　①②这两个组合体的三视图如下：
『规律总结』　画简单组合体的三视图时要注意的问题：(1)分清简单组合体是由哪些简单几何体组成的，是组合型还是切挖型．(2)先画主体部分，后画次要部分．(3)几个视图要配合着画．一般是先画主视图再确定左视图和俯视图．(4)组合体的各部分之间要画出分界线．
〔跟踪练习2〕画出如图所示的几何体的三视图．
命题方向3　⇨由三视图还原空间几何体
　　　　　一个几何体的三视图如图所示，请画出它的直观图．
[思路分析]　解答本题可先根据三视图所提供的信息，应用三视图的相关概念，再进行逆推还原，从而使问题得解．
[解析]　由三视图可知，该几何体如图所示．
『规律总结』　1.由三视图到立体图形，要仔细分析和观察三视图，充分想象，看图和想图是两个重要步骤．“想”在“看”中，形体分析的看图方法是解决此类还原问题的常用方法．2．原几何体的轮廓线的长度与三视图长度之间的关系易混淆．
〔跟踪练习3〕根据如图所示中物体的三视图，画出该物体．
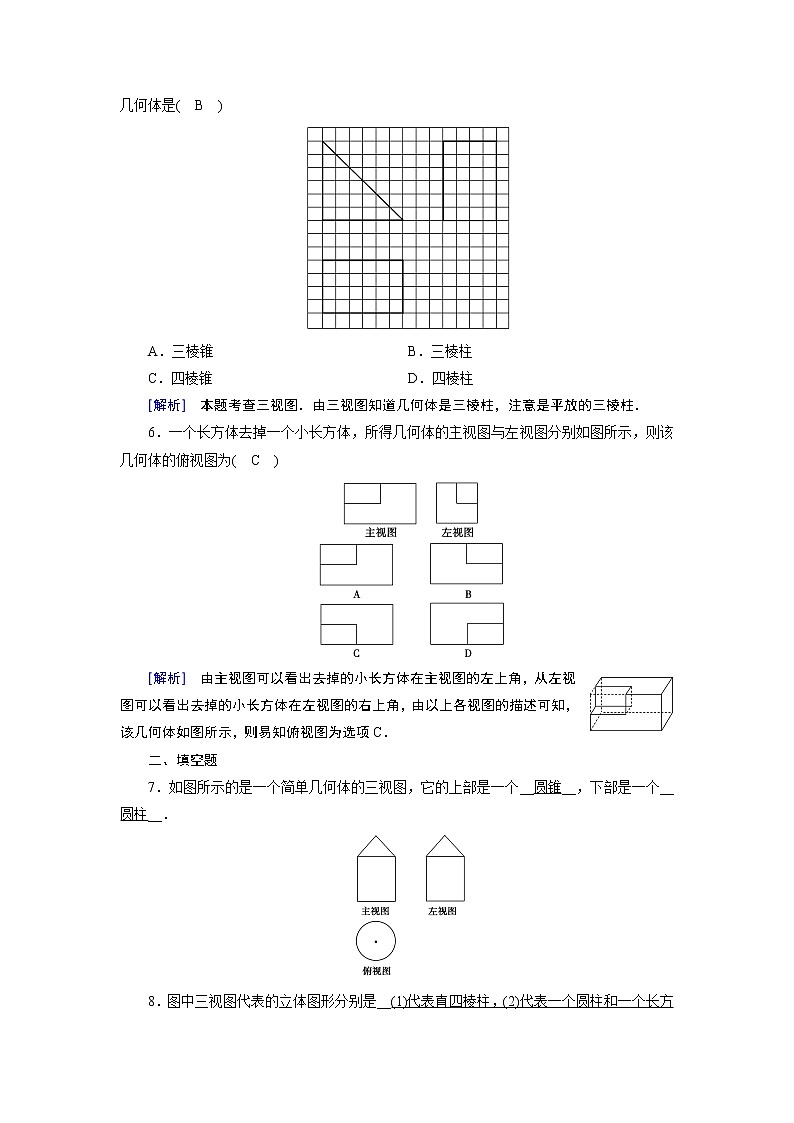
[解析]　由主视图可以判断出这个几何体由两部分构成，由左视图可以判断出上下两部分的宽度是相等的，再由俯视图可以判断出这个几何体的上部分是一个圆柱，下部分是一个长方体．
命题方向4　⇨由三视图求几何体的相关量
　　　　　若一个正三棱柱的三视图如图所示，求这个三棱柱的高和底面边长以及左视图的面积．
[思路分析]　根据三视图提供的信息，可得正三棱柱的高和底面正三角形的高，从而可求底面边长以及左视图的面积．
『规律总结』　解决三视图中有关量的计算问题时，首先要明确三视图在度量上的特点：主左一样高，主俯一样长，俯左一样宽，据此可互求三视图中有关线段的长度．其次要明确三视图对应的原几何体在度量上的特点，获得原几何体中相关的量，从而进行计算．
1．识画三视图的关键是弄清方位，确定前后，左右位置关系，抓住垂直关系．2．由三视图还原空间几何体的策略(1)通过主视图和左视图确定是柱体、锥体还是台体．若主视图和左视图为矩形，则原几何体为柱体；若主视图和左视图为等腰三角形，则原几何体为锥体；若主视图和左视图为等腰梯形，则原几何体为台体，另外需注意非正常位置放置的常见几何体的三视图特征．(2)通过俯视图确定是多面体还是旋转体．若俯视图为多边形，则原几何体为多面体；若俯视图为圆，则原几何体为旋转体．
空间想象能力——识图、画图、用图　　
3．由三视图还原空间几何体的步骤
　　　　　根据下列图中所给出的几何体的三视图，试画出它们的形状．
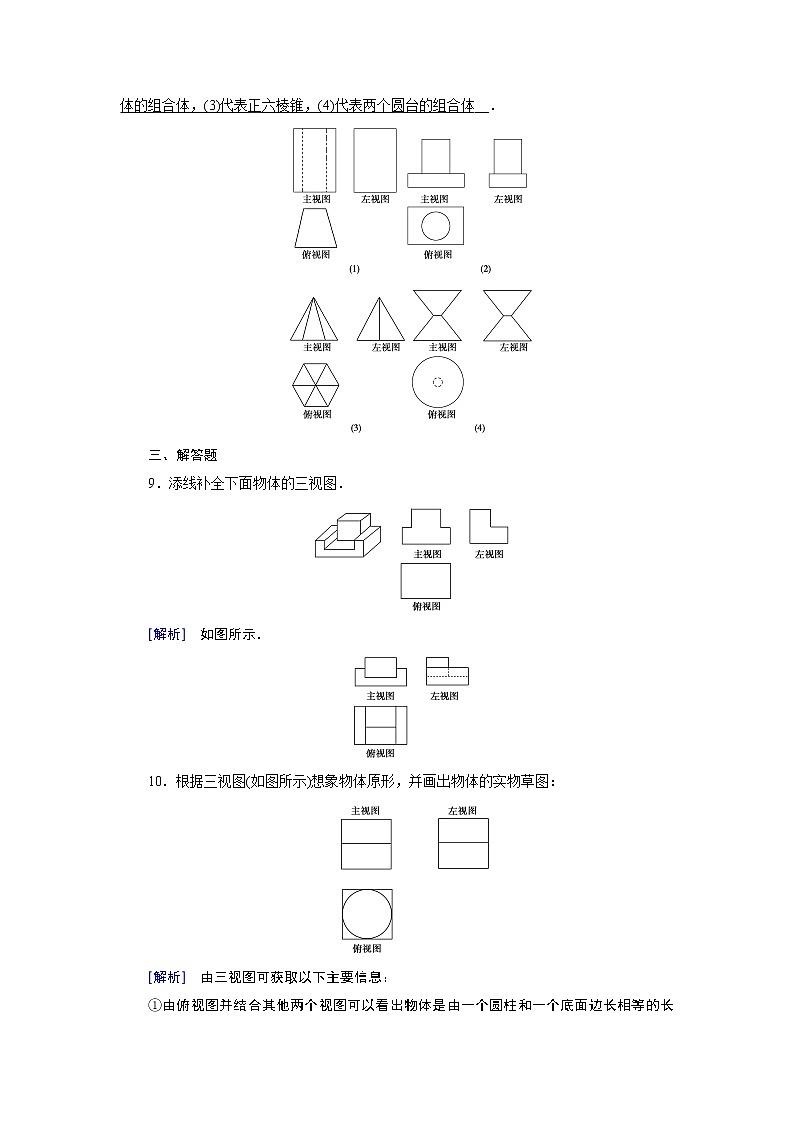
[解析]　图(1)对应的几何体是一个六棱锥，图(2)对应的几何体是一个三棱柱，则所对应的空间几何体的图形分别为：
〔跟踪练习5〕一个几何体的三视图如图所示．则该几何体的直观图可以是(　　)
[解析]　由俯视图易知，只有选项D符合题意．故选D．
　　　　　画出如图所示物体的三视图．
[错解]　如图所示．[辨析]　被挡住的部分没有画出并且丢掉一些边．
『规律总结』　在画由基本几何体拼接而成的组合体的三视图时，除了要注意三视图的排列规则和特点外，最重要的是看清该组合体由哪几个基本几何体拼接而成，找准其表面的交线，即分界线，用实线画出．
课 时 作 业 学 案