


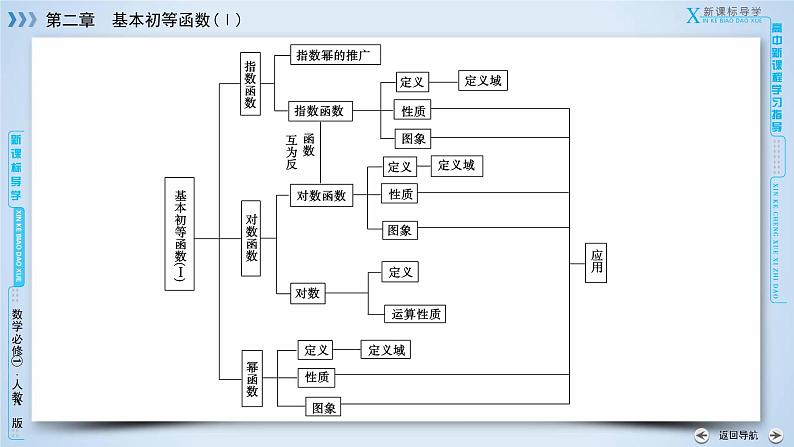



高中数学人教版新课标A必修1第二章 基本初等函数(Ⅰ)综合与测试教案配套ppt课件
展开1.指数幂、对数式的运算、求值、化简、证明等问题主要依据指数幂、对数的运算性质,在进行指数、对数的运算时还要注意相互间的转化.2.指数函数和对数函数的性质及图象特点是这部分知识的重点,而底数a的不同取值对函数的图象及性质的影响则是重中之重,要熟知a在(0,1)和(1,+∞)两个区间取值时函数的单调性及图象特点.3.应用指数函数y=ax和对数函数y=lgax的图象和性质时,若底数含有字母,要特别注意对底数a>1和0
7.求含有指数函数和对数函数复合函数的最值或单调区间时,首先要考虑指数函数、对数函数的定义域,再由复合函数的单调性来确定其单调区间,要注意单调区间是函数定义域的子集.其次要结合函数的图象,观察确定其最值或单调区间.8.函数图象是高考考查的重点内容,在历年高考中都有涉及.考查形式有知式选图、知图选式、图象变换以及用图象解题.函数图象形象地显示了函数的性质,利用数形结合有时起到事半功倍的效果.
专题一 ⇨指数、对数的运算
指数式的运算首先要注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂;其次若出现分式,一要注意分母与负指数的关系;二要注意把分子、分母因式分解以达到约分的目的.对数运算首先要注意公式应用过程中范围的变化,前后要等价;其次要熟练地运用对数的三个运算性质,并根据具体问题合理利用对数恒等式和换底公式等.换底公式是对数计算、化简、证明常用的公式,一定要掌握并灵活运用.
『规律方法』 指数与对数的运算是指数、对数应用的前提,也是研究指数函数与对数函数的基础,不仅是本章考查重点,也是高考的重要考点之一.进行指数式的运算时,要注意运算或化简的先后顺序,一般应将负指数转化为正指数、将根式转化为指数式后再计算或化简,同时注意幂的运算性质的应用;对数运算要注意对数运算性质的正用与逆用,注意对底数的转化,对数恒等式以及换底公式的灵活运用,还要注意对数运算与指数运算之间的关系及其合理地转化.
专题二 ⇨指数(对数)函数的典型问题及其求解策略
指数函数y=ax(a>0且a≠1)与对数函数y=lgax(a>0且a≠1)的性质及图象对比.(1)两者具有相同的单调性,a>1时单调递增,0
『规律方法』 (1)有关比较大小的问题,通常需要结合所给的数的特点,结合相关函数的性质,通过寻找合适的中间数,确定其大小关系.(2)通常解决此类问题的关键是先化为统一类型的形式(比如都为同底的),然后再根据函数的单调性比较,特殊情况还要和1或0比较.
『规律方法』 1.两类对数不等式的解法(1)形如lgaf(x)
专题三 ⇨思想方法总结
1.数形结合思想数形结合思想的基本思路:根据数的结构特征,构造出与之相应的几何图形,并利用图形的特征和规律,解决数的问题,或将图形信息转化成代数信息,使解决形的问题转化为数量关系的问题讨论.
(2019·北京丰台区高一期末测试)已知等式lg2m=lg3n(m>0,n>0)成立,那么下列结论:①m=n;②n
3.转化与化归思想转化思想是在处理问题时,把那些待解决或难解决的问题,通过某种转化过程,归结为一类已经解决或比较容易解决的问题,最终求得原问题的解答,转化与化归思想的原则:化繁为简,化难为易,化生为熟.
设a∈R,试讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实根个数.
『规律方法』 将求方程解的问题转化为求对应函数图象交点问题,这种思想方法非常重要,尤其是方程等号两边为不同特征的函数时常用此法来解决.
高中人教版新课标A第二章 统计综合与测试课堂教学课件ppt: 这是一份高中人教版新课标A第二章 统计综合与测试课堂教学课件ppt,共38页。PPT课件主要包含了第二章,章末整合提升,知识网络,专题突破,典例1,典例2,典例3,典例4,典例5,典例6等内容,欢迎下载使用。
高中人教版新课标A第三章 函数的应用综合与测试集体备课ppt课件: 这是一份高中人教版新课标A第三章 函数的应用综合与测试集体备课ppt课件,共6页。
高中数学人教版新课标A必修1第三章 函数的应用综合与测试教案配套课件ppt: 这是一份高中数学人教版新课标A必修1第三章 函数的应用综合与测试教案配套课件ppt,共30页。PPT课件主要包含了第三章,函数的应用,章末整合提升,知识结构,要点归纳,专题突破,典例1,典例2,典例3,典例4等内容,欢迎下载使用。














