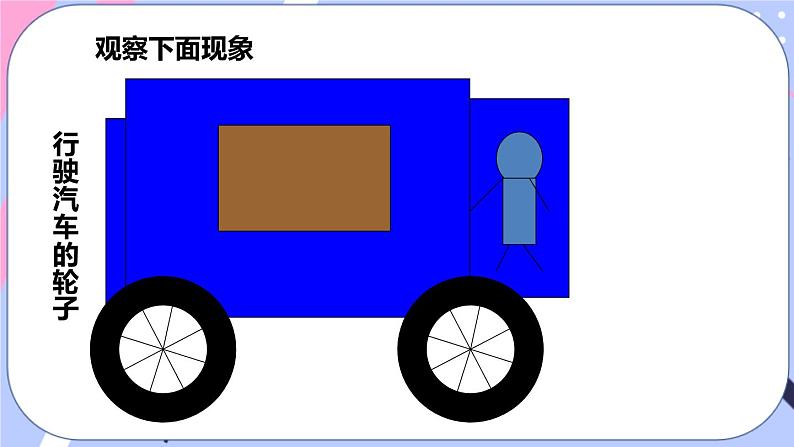
2020-2021学年2 图形的旋转试讲课课件ppt

这是一份2020-2021学年2 图形的旋转试讲课课件ppt，共25页。PPT课件主要包含了它们是怎样变过来的，观察下面现象，行驶汽车的轮子，定点O叫做旋转中心，转动的角叫做旋转角，典例赏析，旋转的基本性质，做一做，想一想，或120等内容，欢迎下载使用。

1 通过具体实例认识平面图形的旋转；2 探索图形旋转的基本性质；（重点）3 会进行简单的旋转画图.（难点）
“平移图案”的形成方法：
(1)确定“基本图案”：
(2)构建“平移图案”：
由“基本图案”通过平移得到.
你能否描述一下什么叫旋转？
定义：在平面内，将一个图形绕着一个定点沿某个方向转动一个角度，这样的图形运动称为旋转.这个定点称为旋转中心，转动的角称为旋转角。
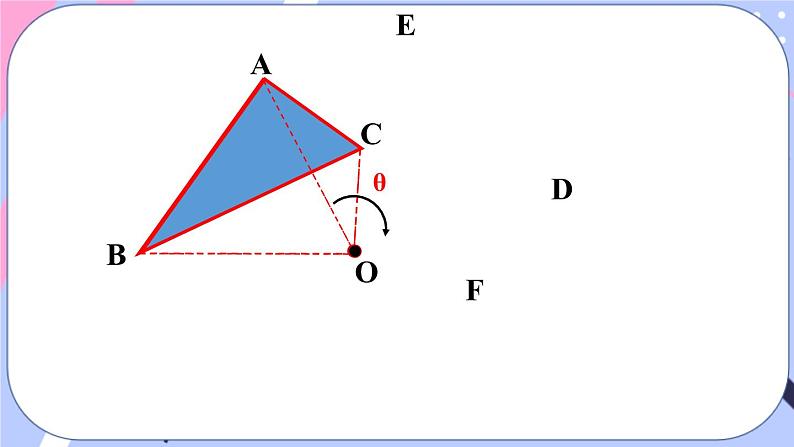
点A与点D是一组对应点，线段AB与线段DE是一组对应线段，∠BAC与∠EDF是一组对应角.
△ ABC绕点O顺时针方向旋转到△DEF, 点A,B,C分别旋转到了点 D,E,F.
例1 下列运动属于旋转的是(　　)A．篮球的滚动 B．钟摆的摆动C．气球升空的运动 D．一个图形沿某条直线对折的过程
总结：判断一种运动是否是旋转的前提条件是图形在同一平 面内的运动，其次要紧扣旋转的“三要素”，看是否同时具有：旋转中心、旋转角、旋转方向．
线： AO=A'O ，BO=B'O ，CO=C'O
角;∠AOA'=∠BOB' =∠COC'
(4)对应点到旋转中心的距离相等．
(1)旋转不改变图形的大小和形状．
(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.
(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角．
（旋转不改变图形的形状和大小）
如图所示，如果把钟表的指针看作四边形AOBC，它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中：
(2)经过旋转，点A，B，C分别移到什么位置？
(1)旋转中心是什么？旋转方向是什么？
(3)它们转动的方向和角度又怎样？
(5)AO与DO的长有什么关系？BO与EO，CO与FO呢 ？
(4)∠AOD、∠BOE、∠COF有什么大小关系？
一个图形和它经过旋转所得的图形中，对应点到旋转中心的距离相等，任意一组对应点与旋转中心的连线所成的角都等于旋转角；对应线段相等，对应角相等.
在下图的四个三角形中，哪个不能由△ABC经过平移或旋转得到？
例2 如图，Rt△ABC中，已知∠C＝90°，∠B＝50°，点D在边BC上，BD＝2CD．把 △ABC绕着点D逆时针旋转m(0＜m＜180)度后，如果点B恰好落在初始Rt△ABC的边上，那么m＝ ________.
解析：本题可以将图形的旋转问题转化为点B绕D点逆时针旋转的问题，如图，以D点为圆心，DB长为半径画弧，与Rt△ABC交斜边AB于一点B′，交直角边AC于B″，连接B′D，B″D，此时B′D＝BD，B″D＝BD＝2CD.由等腰三角形的性质求旋转角∠BDB′的度数；在Rt△B″CD中，由B″D＝2CD，可得∠CB″D＝30°，从而求出∠CDB″的度数，进而可得旋转角∠BDB″的度数．
1 下列现象中属于旋转现象的是(　　)A．钟摆的摆动 B．飞机在飞行C．汽车在奔跑 D．小鸟的飞翔
2 如图，△ABC和△ADE均为等边三角形，则图中可以看成是旋转关系的三角形是(　　)A．△ABC和△ADE B．△ABC和△ABDC．△ABD和△ACE D．△ACE和△ADE
3 在俄罗斯方块游戏中，已拼好的图案如图所示，现又出现一小方格体正向下运动，为了使所有图案消失，你必须进行以下哪项操作，才能拼成一个完整图案，使其自动消失(　　)A．顺时针旋转90°，向右平移B．逆时针旋转90°，向右平移C．顺时针旋转90°，向下平移D．逆时针旋转90°，向下平移
4 如图，若将△ABC绕点O逆时针旋转90°，则顶点B的对应点B1的坐标为(　　)A．(－4，2) B．(－2，4)C．(4，－2) D．(2，－4)
5 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠1＝25°，则∠BAA′的度数是(　　)A．55° B．60° C．65° D．70°
在平面内，将一个图形绕一个定点按某个方向转动一个角度，这样的图形运动称为旋转(变换).
2、“旋转”的基本性质：
(2)旋转的决定因素： ①旋转中心；②旋转角；③旋转方向．