数学八年级下册第六章 平行四边形1 平行四边形的性质优质课件ppt

这是一份数学八年级下册第六章 平行四边形1 平行四边形的性质优质课件ppt，共24页。PPT课件主要包含了两组对边都不平行，两组对边分别平行，四边形，平行四边形，典例赏析，平行四边形的性质，如何证明等内容，欢迎下载使用。

1 知道平行四边形的有关概念.（重点）2 掌握平行四边形的性质(中心对称图形、对边相等、对角相等).（重点）
这些都是日常生活中常见的情形，它们是否都具有相似的特征？
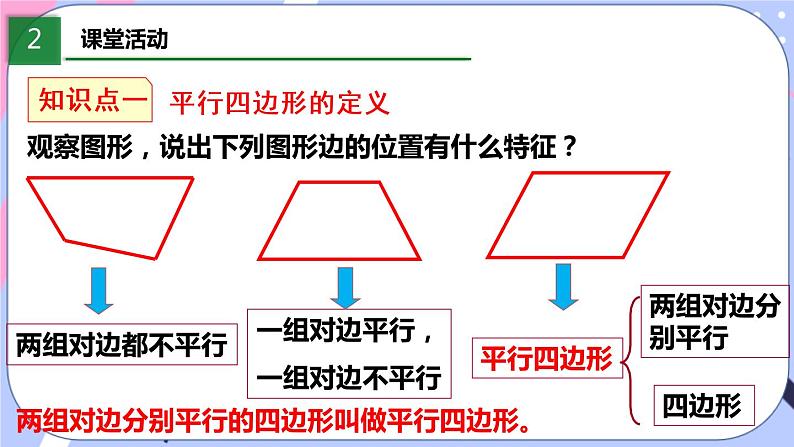
一组对边平行，一组对边不平行
两组对边分别平行的四边形叫做平行四边形。
观察图形，说出下列图形边的位置有什么特征？
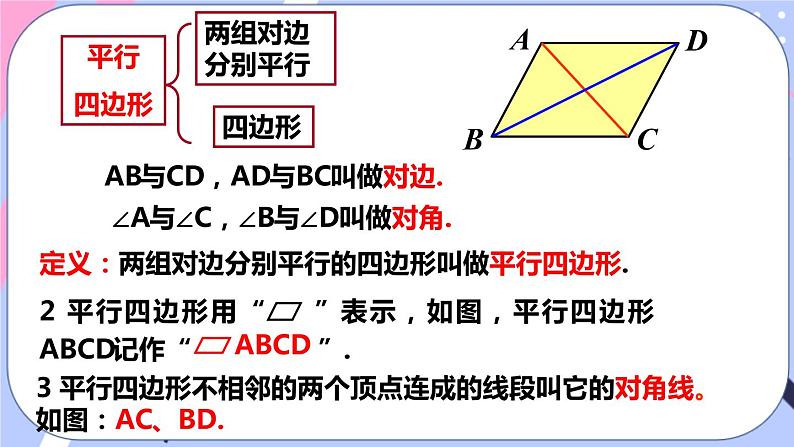
∠A与∠C，∠B与∠D叫做对角.
AB与CD，AD与BC叫做对边.
3 平行四边形不相邻的两个顶点连成的线段叫它的对角线。如图：AC、BD.
定义：两组对边分别平行的四边形叫做平行四边形.
平行四边形是中心对称图形，不是轴对称图形，并且平行四边形两条对角线的交点是它的对称中心；平行四边形的邻角互补.
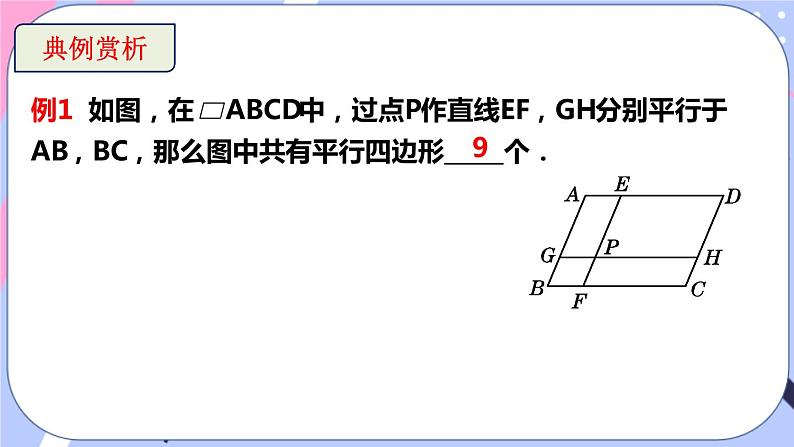
例1 如图，在 ABCD中，过点P作直线EF，GH分别平行于AB，BC，那么图中共有平行四边形_____个．
平行四边形的对称性.平行四边形是轴对称图形吗？是中心对称图形吗？如果是，你能找出它的对称中心、对称轴吗？
平行四边形是中心对称图形，两条对角线的交点是它的对称中心.
1 平行四边形的边具有哪些性质？说说你的理由。
2 平行四边形的角具有哪些性质？说说你的理由。
１ 平行四边形的对边相等
２ 平行四边形的对角相等．
边的性质：平行四边形对边平行；平行四边形对边相等．数学表达式：如图，∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，AB＝CD，AD＝BC.
例2 已知：如图(1)，四边形ABCD是平行四边形.求证：AB＝CD，BC＝DA.
证明：连接AC(如图(2)).∵四边形ABCD是平行四边形，∴ AB∥CD，BC∥DA(平行四边形的定义）.∴∠1＝∠2,∠3＝∠4.∵AC＝CA，∴△ABC≌△CDA. ∴AB＝CD，BC＝DA.
1 角的性质：平行四边形对角相等；平行四边形邻角互补．数学表达式：如图，∵四边形ABCD是平行四边形，∴∠A＝∠C，∠B＝∠D.∴∠A＋∠B＝180°，∠B＋∠C＝180°，∠C＋∠D＝180°，∠A＋∠D＝180°.
例3 已知：如图，在 ABCD中，E，F是对角线AC上的两点，并且AE=CF.求证：BE=DF.
证明：∵四边形ABCD是平行四边形，∴AB=CD（平行四边形的对边相等） AB∥CD（平行四边形的定义）.∴∠BAE=∠DCF.又∵AE=CF，∴△ABE≌△CDF.∴BE=DF.
1 在▱ABCD中，∠A＋∠C＝200°，则∠B的度数是(　　)A．100° B．160° C．80° D．60°
2 如图，在▱ABCD中，连接AC，∠ABC＝∠CAD＝45°，AB＝2，则BC的长是(　　)A. B．2 C．2 D．4
3 如图，在▱ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，若△CED的周长为6，则▱ABCD的周长为(　　)A．6 B．12 C．18 D．24
4 如图，在▱ABCD中，BM是∠ABC的平分线，交CD于点M，且MC＝2，▱ABCD的周长是14，则DM等于(　　)A．1 B．2 C．3 D．4
5 如图，E，F分别是▱ABCD的边AD，BC上的点，EF＝6，∠DEF＝60°，将四边形EFCD沿EF翻折，得到四边形EFC′D′，ED′交BC于点G，则△GEF的周长为(　　)A．6 B．12 C．18 D．24
(1)如果AE＝2，求CD的长；(2)如果∠AEB＝40°，求∠C的度数.