北师大版七年级下册1 两条直线的位置关系课时练习

这是一份北师大版七年级下册1 两条直线的位置关系课时练习，共7页。
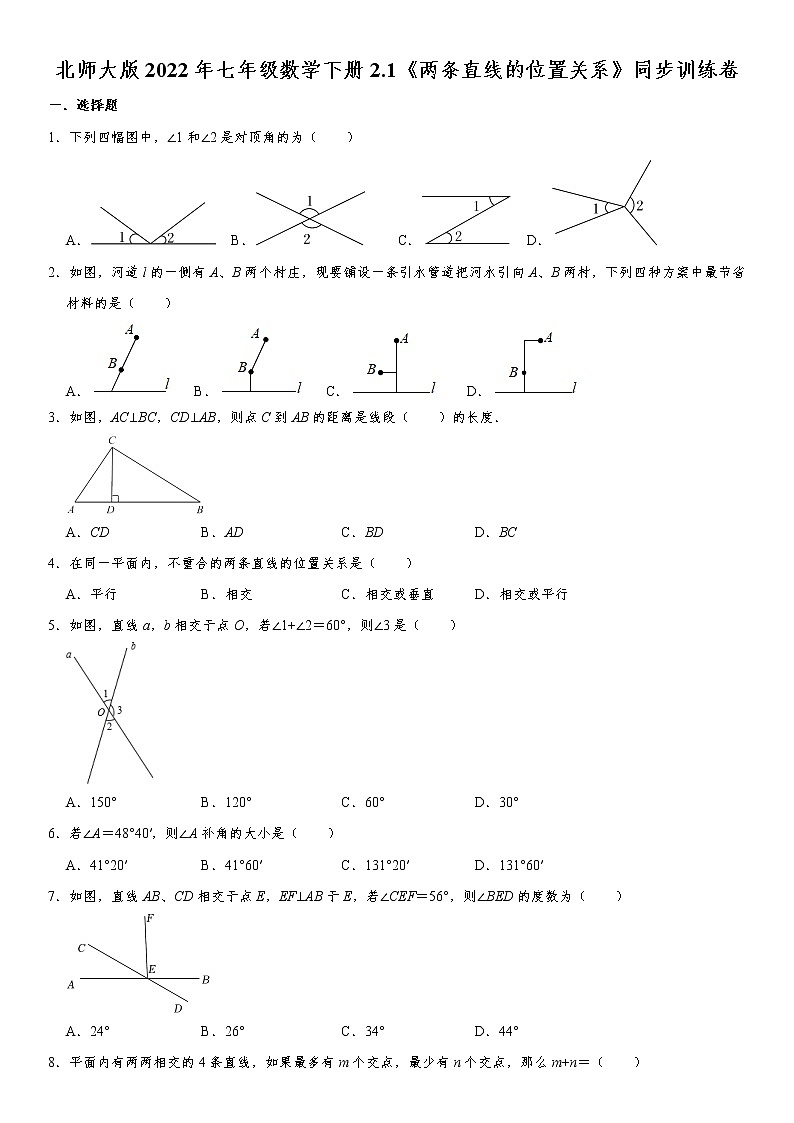
1．下列四幅图中，∠1和∠2是对顶角的为（ ）
A． B． C． D．
2．如图，河道l的一侧有A、B两个村庄，现要铺设一条引水管道把河水引向A、B两村，下列四种方案中最节省材料的是（ ）
A． B． C． D．
3．如图，AC⊥BC，CD⊥AB，则点C到AB的距离是线段（ ）的长度．
A．CDB．ADC．BDD．BC
4．在同一平面内，不重合的两条直线的位置关系是（ ）
A．平行B．相交C．相交或垂直D．相交或平行
5．如图，直线a，b相交于点O，若∠1+∠2＝60°，则∠3是（ ）
A．150°B．120°C．60°D．30°
6．若∠A＝48°40′，则∠A补角的大小是（ ）
A．41°20′B．41°60′C．131°20′D．131°60′
7．如图，直线AB、CD相交于点E，EF⊥AB于E，若∠CEF＝56°，则∠BED的度数为（ ）
A．24°B．26°C．34°D．44°
8．平面内有两两相交的4条直线，如果最多有m个交点，最少有n个交点，那么m+n＝（ ）
A．9B．8C．7D．6
二．填空题
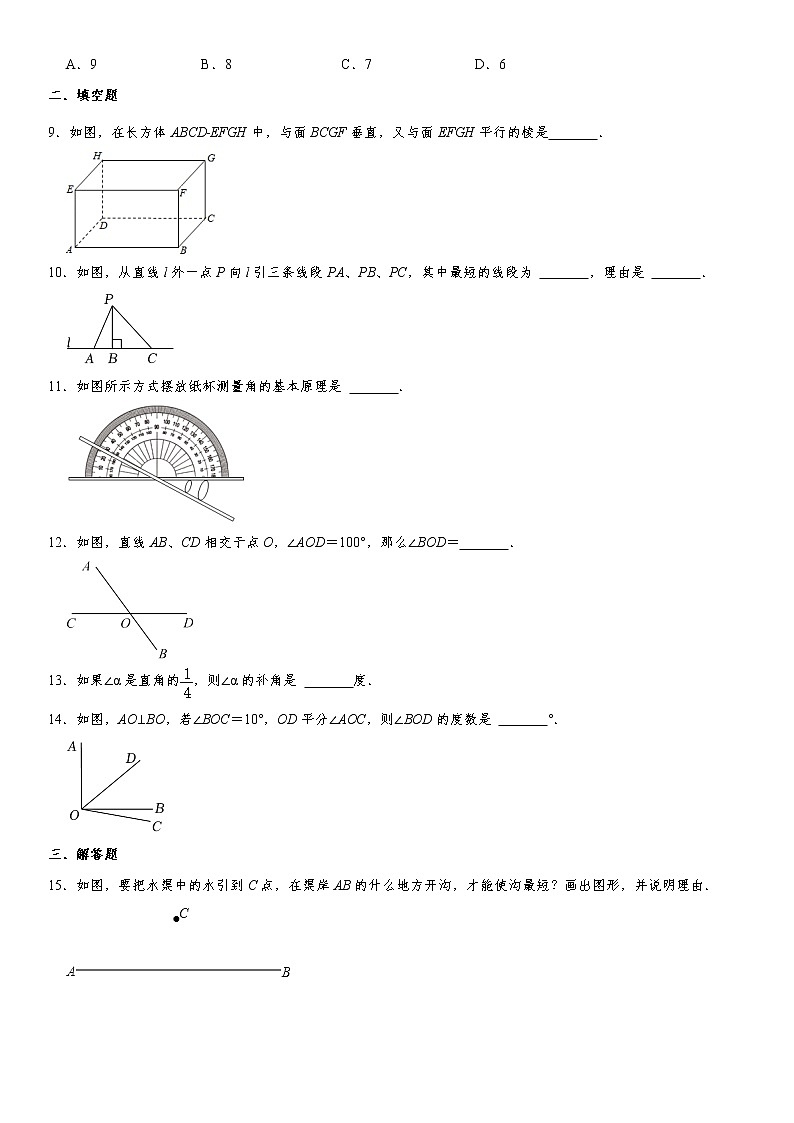
9．如图，在长方体ABCD﹣EFGH中，与面BCGF垂直，又与面EFGH平行的棱是 ．
10．如图，从直线l外一点P向l引三条线段PA、PB、PC，其中最短的线段为 ，理由是 ．
11．如图所示方式摆放纸杯测量角的基本原理是 ．
12．如图，直线AB、CD相交于点O，∠AOD＝100°，那么∠BOD＝ ．
13．如果∠α是直角的，则∠α的补角是 度．
14．如图，AO⊥BO，若∠BOC＝10°，OD平分∠AOC，则∠BOD的度数是 °．
三．解答题
15．如图，要把水渠中的水引到C点，在渠岸AB的什么地方开沟，才能使沟最短？画出图形，并说明理由．
16．如图，O是直线AB上一点，OC为任意一条射线，OD平分∠BOC，OE平分∠AOC．
（1）图中∠AOD的补角是 和 ；∠BOD的余角是 和 ．
（2）已知∠COD＝40°，求∠COE的度数．
17．如图：
（1）如图1，两条直线相交，最多有 个交点；
如图2，三条直线相交，最多有 个交点；
如图3，四条直线相交，最多有 个交点；
如图4，五条直线相交，最多有 个交点；
（2）归纳，猜想，n条直线相交，最多有 个交点．
18．如图1，OB、OC是∠AOD内部两条射线．
（1）若∠AOD和∠BOC互为补角，且∠AOD＝2∠BOC，求∠AOD及∠BOC的度数；
（2）如图2，若∠AOD＝2∠BOC，在∠AOD的外部分别作∠COD、∠AOB的余角∠DOM及∠AON，请写出∠DOM、∠AON、∠BOC之间的数量关系，并说明理由；
（3）如图3，已知∠AOD＝120°，射线OE平分∠AOD，若将OB绕O点从OA出发以每秒6°逆时针旋转，OC绕O点从OD出发以每秒5°顺时针旋转，OB、OC同时运动；当OC运动一周回到OD时，OB、OC同时停止运动．若运动t（t＞0）秒后，OE恰好是∠BOC的四等分线，则此时t的值为 （直接写出答案）．
参考答案
一．选择题
1．解：由对顶角的定义可知，
选项B中的∠1与∠2是对顶角，
故选：B．
2．解：依据垂线段最短，以及两点之间，线段最短，可得最节省材料的是：
故选：B．
3．解：∵CD⊥AB，
∴点C到AB的距离是线段CD的长度，
故选：A．
4．解：在同一平面内，不重合的两条直线的位置关系是相交或平行，相交包含垂直．
故选：D．
5．解：∵∠1+∠2＝60°，∠1＝∠2（对顶角相等），
∴∠1＝30°，
∵∠1与∠3互为邻补角，
∴∠3＝180°﹣∠1＝180°﹣30°＝150°．
故选：A．
6．解：∠A的补角＝180°﹣48°40′＝131°20′．
故选：C．
7．解：∵EF⊥AB于E，∠CEF＝56°，
∴∠AEC＝90°﹣∠CEF＝90°﹣56°＝34°，
∴∠BED＝∠AEC＝34°．
故选：C．
8．解：如图所示：
4条直线两两相交，有3种情况：4条直线经过同一点，有一个交点；3条直线经过同一点，被第4条直线所截，有4个交点；4条直线不经过同一点，有6个交点．
故平面内两两相交的4条直线，最多有6个交点，最少有1个交点；即m＝6，n＝1，则m+n＝7．
故选：C．
二．填空题
9．解：如图，在长方体ABCD﹣EFGH中，与面BCGF垂直，又与面EFGH平行的棱是棱AB，棱CD．
故答案为：棱AB，棱CD．
10．解：从直线l外一点P向l引三条线段PA、PB、PC，其中最短的线段为PB，依据是垂线段最短，
故答案为：PB，垂线段最短．
11．解：图中的测量角的原理是：对顶角相等．
故答案为：对顶角相等．
12．解：∵∠AOD＝100°，∠BOC与∠AOD是对顶角，
∴∠BOC＝∠AOD＝100°，
∵∠BOC+∠BOD＝180°，
∴∠BOD＝80°．
故答案为：80°．
13．解：∵∠α是直角的，
∴∠α＝×90°＝22.5°，
∴∠α的补角为：180°﹣22.5°＝157.5°，
故答案为：157.5．
14．解：因为OA⊥OB，
所以∠AOB＝90°，
因为∠BOC＝10°，
所以∠AOC＝∠AOB+∠BOC＝90°+10°＝100°，
因为OD平分∠AOC，
所以∠COD＝∠AOC＝50°，
所以∠BOD＝∠COD﹣∠COB＝50°﹣10°＝40°，
故答案为：40．
三．解答题
15．解：如图，过C作CD⊥AB，垂足为D，
在D处开沟，则沟最短．
因为直线外一点与直线上各点连线的所有线段中，垂线段最短．
16．解：（1）∵OD平分∠BOC，OE平分∠AOC，
∴∠BOD＝∠COD，∠AOE＝∠COE，
∴∠EOC+∠COD＝∠AOE+∠BOD＝90°，
∴∠BOD+∠EOC＝90°，
∵∠AOD+∠BOD＝180°，
∴∠AOD+∠COD＝180°，
∴∠AOD的补角是∠BOD和∠COD；∠BOD的余角是∠COE和∠AOE．
故答案为：∠BOD，∠COD；∠COE，∠AOE．
（2）∵OD平分∠BOC，∠COD＝40°，
∴∠BOC＝2∠COD＝80°，
由题意可知，∠AOB是平角，∠AOB＝∠AOC+∠BOC，
∴∠AOC＝∠AOB﹣∠BOC
＝180°﹣80°
＝100°，
∵OE平分∠AOC，
∴∠COE＝∠AOC＝50°．
17．解：（1）如图1，两条直线相交，最多有1个交点；
如图2，三条直线相交，最多有3个交点；
如图3，四条直线相交，最多有6个交点；
如图4，五条直线相交，最多有10个交点；
故答案为：1，3，6，10；
（2）归纳，猜想，n条直线相交，最多有个交点．
故答案为：．
18．解：（1）∵∠AOD和∠BOC互为补角，
∴∠AOD+∠BOC＝180°，
∵∠AOD＝2∠BOC，
∴3∠BOC＝180°，
∴∠BOC＝60°，∠AOD＝120°．
（2）∠DOM+∠AOA+∠BOC＝180°，
设∠BOC＝α，则∠AOD＝2α，
∵∠DOM和∠AON分别是∠COD和∠AOB的余角，
∴∠DOM+∠COD+∠AON+∠AOB＝180°，
∴∠AOB+∠COD＝∠AOD﹣∠BOC＝2α﹣α＝α，
∠DOM+∠AON＝180°﹣α，
∴∠DOM+∠AON+∠BOC＝180°﹣α+α＝180°．
（3）①OB到达OE前，如图3①，
由点的运动可知，∠AOB＝6°t，∠DOC＝5°t，
∴∠BOC＝120°﹣6°t﹣5°t＝120°﹣11°t，∠BOE＝60°﹣6°t，∠COE＝60°﹣5°t，
由题意可知，120°﹣11°t＝4（60°﹣6°t），解得t＝，
②当射线OC到达射线OE后，如图3②，
此时，∠COE＝5°t﹣60°，∠BOE＝6°t﹣60°，
则∠BOC＝∠COE+∠BOE＝11°t﹣120°，
根据题意可知，4（5°t﹣60°）＝11°t﹣120°，解得t＝；
③当射线OB旋转一周后，如图3③，
此时，∠COE＝360°﹣5°t+60°＝420°﹣5°t，∠BOE＝60°﹣（360°﹣6°t）＝6°t﹣360°，
∴∠BOC＝∠COE+∠BOE＝60°+t，
根据题意得，4（6°t﹣360°）＝60°+t，解得t＝．
故答案为：或或．